自然电位测井数值计算中的激励源分布

范晓敏，李舟波

吉林大学地球探测科学与技术学院，长春 130026

自然电位测井数值计算中的激励源分布

范晓敏，李舟波

吉林大学地球探测科学与技术学院，长春 130026

为实现自然电位测井的高效正演计算，以定量研究各种因素影响，针对自然电位的激励源——偶电层的分布进行了研究。通过对自然电位产生原因及偶电层对自然电位贡献的分析，认为只有泥岩井壁、侵入带中砂泥岩界面和侵入带与原状地层分界面处的偶电层对自然电位测井值有贡献，而研究砂岩层处的自然电位异常，则仅考虑由侵入带与原状地层界面处的偶电层即可。通过直流电场与静电场的类比，推出了偶极源的面电流密度表达式，并通过计算研究了均匀介质中侵入深度的影响。结果显示，自然电位曲线形状随侵入深度增加而变得平缓，异常幅度减小。

自然电位测井；偶电层；电化学电动势；侵入深度影响

自然电位测井是实际生产中使用最多的常规测井方法之一，目前在储层定性识别和泥质含量估计方面起重要作用，随着数值模拟研究的深入，自然电位还将为侵入带研究和储层参数计算提供有用信息［1］。同时，储层定量评价的深入发展和充分利用所有测井信息解决复杂储层评价工作也要求自然电位测井的高精度数值模拟。自然电场所满足的方程与直流电阻率法相同，但自然电位测井中场源的处

理较为复杂，这也是造成其数值模拟工作远远少于电阻率测井的一个原因。一般自然电位的场源可以归结为偶电层来考虑，但对于钻井穿过砂泥岩剖面后偶电层的分布，文献中有不同的假设：一种认为只是在有浓度差的位置才有偶电层；另一种认为除了浓度差，一些岩性界面，包括泥岩表面也存在偶电层。对于后一种假设，要处理砂岩和泥岩的整个接触面。Guyod［2］给出了3种等效模型，但没有相应的分析和解释。自然电位测井的数值模拟可采用有限差分法［3－4］、有限元法［5］和模式匹配法［6］等，这些方法都需要在模型中给定偶电层的位置和电动势数值或激励源的电流密度值。笔者通过对影响自然电位数值的双电层分布进行分析，认为只有存在浓度差的偶电层才能影响自然电位测井的数值，而其他偶电层在计算中不必考虑。

1 偶电层的产生和分布

关于石油测井中自然电位产生的原因，目前公认的理论认为是电化学电动势引起的，包括砂岩中由于浓度差引起的扩散电位和泥岩中的薄膜电位。扩散电位是在砂岩两侧溶液存在浓度差时，离子会从浓度高的一侧向浓度低的一侧迁移，由于2种离子的迁移速度不同，造成正、负离子浓度差异，于是在砂岩两侧产生电位差，亦称电动势。薄膜电势稍复杂些，黏土矿物因低价离子置换高价离子等原因而带负电，孔隙溶液中阳离子吸附在黏土矿物表面，从而维持电荷平衡，因此这些阳离子又称平衡离子。由于这些阳离子被吸附在黏土矿物的周围，导致矿物颗粒之间的空隙中溶液的阳离子浓度大于阴离子浓度，形成所谓“扩散层”，泥岩中孔隙尺寸小于“扩散层”厚度。泥岩两侧溶液出现浓度差时，离子会通过泥岩从浓度高的一侧向浓度低的一侧扩散移动，而发生移动的阳离子数多于阴离子，结果造成泥岩两侧正、负离子浓度差异，于是产生电位差［7］。因为在此过程中既涉及浓度差引起的扩散，又与黏土吸附阳离子有关，也有称其为扩散吸附电动势［8］。早期研究发现，空井（无泥浆）中泥岩层相对于砂岩层具有更高的电位［9］，因此有人以此来解释泥岩处自然电位测井值较高的现象。在偶电层分布问题上，目前有2种观点：一种认为只有在浓度差存在的区域才发生偶电层（图1a）；另一种则认为除了浓度差，在砂泥岩界面处也有偶电层存在（图1b）。2种观点的差别就在于，自然电位异常中是否包括砂泥岩地层界面处偶电层的贡献。

2 有效偶电层及其电位差

对于自然电位测井，有效偶电层是指对自然电位测井值有贡献的那些偶电层。自然电位测井测量的是井中测量电极与地面参考电极之间的电位差，它反映井下测量电极的电位随深度的变化，得到的结果是自然电位测井曲线。电位随深度变化的原因是在某种自然电场作用下，钻井泥浆中形成了电流，该电流的流动造成井孔中纵向电位变化；因此，需要找出能够导致井中电流流动的电动势。

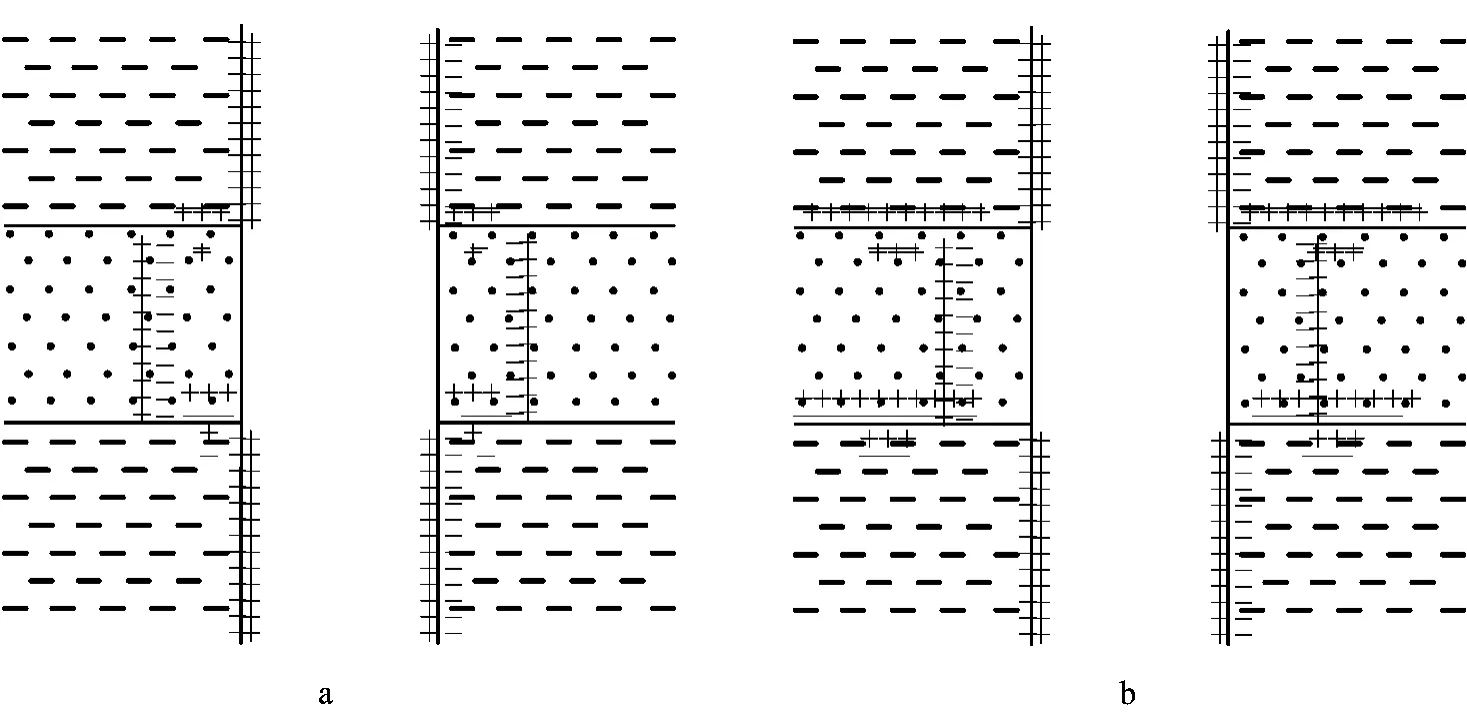
图1 两种典型的偶电层分布模型Fig.1 Two typical models of electric double layers

为分析砂岩和泥岩界面处的偶电层对自然电位测井值的影响，首先考虑没有浓度差的情况，即砂岩孔隙和井孔中都是相同的溶液。这时砂泥岩层界面处的偶电层与泥岩井壁处的偶电层大小相等，方向相反，互相抵消了；由于没有浓度差，扩散电动势也不存在了，于是井中没有自然电流流动，无法测到自然电位异常。泥岩表面围着一个闭合的偶电层面，因为该偶电层两侧的电位差恒定，它对外并不产生电场，因而对自然电位异常没有贡献。

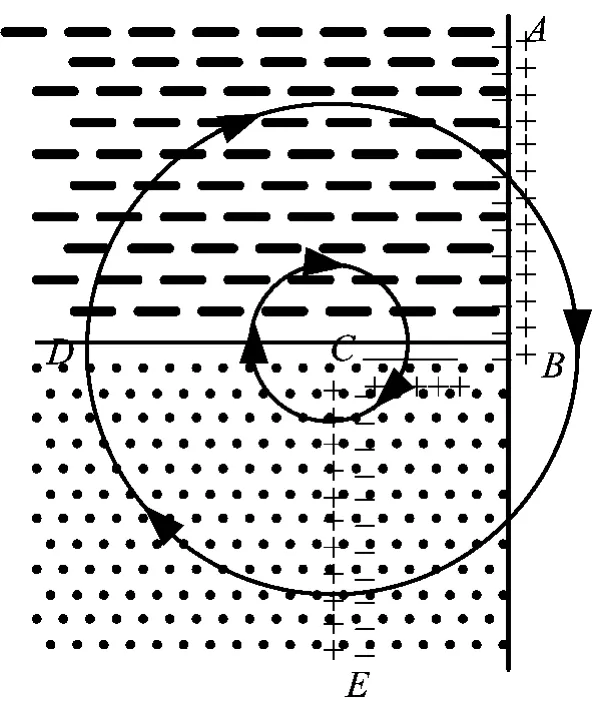
图2 有效偶电层和电流分布示意图Fig.2 Distribution of effective electric double layer and current

其次考虑地下溶液中存在浓度差（比如泥浆滤液与地层水的浓度不同）的情况，这时2种浓度的溶液之间会出现不同符号的电荷聚集而具有电位差。只要浓度差得到维持，电位差就会存在。因为电荷聚集和电位差只出现在浓度变化的区域，并且正、负电荷所带电量相等，所以可认定在水中离子浓度有差异的地方发生偶电层（图2）。在砂泥岩剖面上，渗透性砂岩中偶电层发生在冲洗带与原状地层之间的过渡带（图2中CE），不具渗透性的泥岩层则发生在井壁（图2中AB）处。前者偶电层两侧的电位差是扩散电动势，后者为薄膜电动势，合在一起就是电化学电动势。这时泥岩与砂岩界面处相对于上面的无浓度差情形没有发生任何变化，电位差也没有变化；但泥岩井壁处因为溶液（泥浆）浓度变化，界面偶电层的电位差发生变化，于是整个泥岩表面的偶电层不再是均匀的了，对外产生电场，对于自然电位异常有贡献。为研究问题方便，可以把泥岩井壁的界面电位差看成两部分的和：一部分是由于浓度差造成的电位差，即薄膜电动势；另一部分是没有浓度差情况下的电位差。这样，后一部分可以与砂泥岩地层界面处的偶电层相抵消，对外界电场起作用的就只有泥岩井壁处的薄膜电动势：

式中：Em为薄膜电动势，mV；Km为薄膜电动势系数，mV，与温度和离子成分有关；cw和cmf分别为地层水和泥浆滤液的离子质量分数，10－6。

砂岩和泥岩层界面在侵入带部分与原状地层部分不同，因为该侵入带部分砂岩孔隙中溶液往往不同于地层水。本文不区分冲洗带和侵入带，或者说，侵入带就是冲洗带。这对某些地层会给计算带来一些误差，但因过渡带较薄，误差不会很大。一般情况下，泥浆滤液的电阻率略低于泥浆，其矿化度因泥浆的不同而不同。这是否意味着侵入带这段地层界面（图2中BC）具有不确定性呢？其实泥浆是由泥浆滤液与呈悬浮状态的固体颗粒组成的悬浊液，真正在电化学作用中起作用的溶液只是泥浆滤液，就像砂岩中起作用的是地层水一样。所以，泥浆滤液与泥浆是相同的溶液，BC段界面的电位差与井壁泥岩是一样的，即Em。

由于泥浆渗入地层而在井壁处产生过滤电动势或称动电电动势一般较小，且在泥岩井壁和泥饼（砂岩井壁）处都存在，至少大部分可相互抵消，故对自然电位测井值贡献很小，本文不考虑该电动势。这样，自然电位异常由薄膜电动势和扩散电动势组成，分布在砂岩层中侵入带和原状地层之间的扩散电动势为

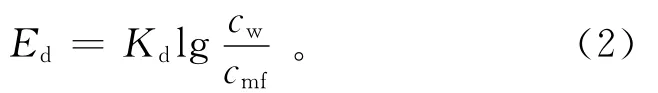
式中：Ed为扩散电动势，mV；Kd为扩散电动势系数，mV，与温度和离子成分有关。

3 偶电层分布的简化

现在已经明确，对自然电位测井值有贡献的偶电层分布在泥岩井壁和侵入带与原状地层的分界面（图3）。图中以灰色标出的是有效偶电层，其深浅差异表明电位差不同。计算时需要处理整个井筒，其中砂岩层的侵入带与原状地层界面还要向地层内缩进一段，工作量较大。下面研究在等效前提下的进一步简化。首先分析无砂岩（无限厚泥岩）情况下的自然电位。在同一油水系统中（地层水成分不变），这时即使井径随深度变化，由于偶电层的电动势为恒定值，井内自然电位是定值，自然电位（VSP）曲线是直线。然后再考虑向地层剖面植入砂岩层，于是出现了自然电位异常，砂岩VSP曲线的异常是在原直线基础上向左（泥浆滤液矿化度低于地层水情况下）偏移的幅度。也就是说，实测自然电位值减去厚层泥岩处的读数（泥岩基线），得到的就是自然电位异常，而这个异常恰好是砂岩层侵入带与原状地层分界面处的偶电层产生的电场造成的。如果在图3a中偶电层的位置整体减去薄膜电动势Em，结果井壁和侵入带中砂泥岩地层界面偶电层被减掉，只剩下砂岩层侵入带与原状地层分界面的偶电层（图3b），但该偶电层的电位差变成

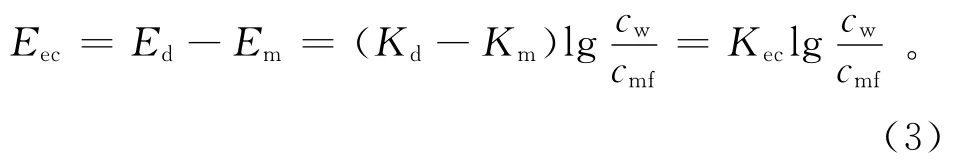
式中：Eec为电化学电动势，mV；Kec是电化学电动势系数，mV。对于NaCl溶液，Em为正值，而Ed为负值，结果Kec为负值（18℃时为－69.6mV）。必须说明，上述简化是在地层水矿化度恒定的条件下进行的，如果地层水发生变化，泥岩基线也会移动，不能这样处理。

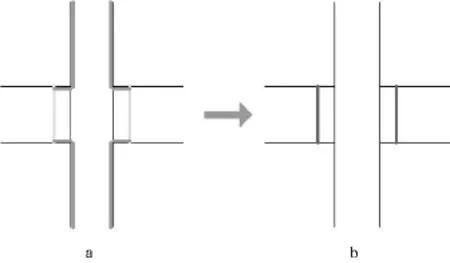
图3 偶电层模型化简Fig.3 Simplication of electric double layer model

4 电偶极层面的电流密度和曲线计算

前面已经给出了偶极源的电动势，在一些数值计算方法中，直接使用该电位差即可，而有些方法则是用电流源更方便，下面利用直流电场与静电场的类比，得出偶极层的电流分布。在地下产生自然电位的源是偶电流层，可看作是由2个贴近的电流面构成［10］。它们的面电流密度分别为i和－i（A／ m2），距离恒定为l（m），则偶电流面的单位面积偶极矩为τ＝il，单位A／m。偶极层两侧电位差为ΔV时，可得到层矩为τ＝ε·ΔV，其中ε为介电常数，F／m。通过类比，可知在稳恒电流场中层矩τ＝σ· ΔV＝ΔV／ρ，其中σ是介质电导率（S／m），ρ是电阻率（Ω·m）。于是得到面电流密度：

在均匀介质中，偶电层产生的电位可以用偶电层对观察点所张开的立体角来计算［11］，空间任一点电位为

式中，Ω是偶层面对观测点所张开的立体角，sr。

图4 不同侵入深度条件下的自然电位测井曲线Fig.4 SP logs for different depths of invasion

利用式（5），可计算出均匀介质条件下不同侵入深度的自然电位曲线，反映侵入深度对VSP曲线的影响。模型为泥岩中间夹一层厚度为2m的砂岩，即111～113m，Eec＝－69.6mV，并假设泥浆、砂岩和泥岩的电阻率相同。图4中的VSP1、VSP3和VSP3分别为侵入带半径等于0.1m、0.3m和0.5m条件下计算的自然电位测井曲线。可以看出，随着侵入深度增加，自然电位测井曲线异常幅度减小，曲线变得平缓，界面反映趋于模糊。

5 结论

1）真正对自然电位测井值有影响的是分布于泥岩井壁、侵入带中砂泥岩界面和侵入带与原状地层分界面处的偶电层，前2个偶电层的电位差为薄膜电动势，最后一个为扩散电动势。

2）在地层水矿化度不变的条件下，如果仅研究砂岩层的自然电位曲线异常，只要计算侵入带与原状地层分界面处的偶电层的贡献即可，其电位差在数值上等于其电化学电动势。

3）影响自然电位曲线的偶电层实际上是2个符号相反的面电流层面，它们的面电流密度为i＝Eec／（lp）。

4）仅考虑侵入带与原状地层分界面偶电层的计算方法可以正确计算出自然电位曲线异常；泥浆侵入越深，自然电位曲线异常幅度越小，曲线越平缓。

（References）：

［1］ 张冲，毛志强，肖亮，等.利用测井资料计算阳离子交换量Qv的方法对比［J］.吉林大学学报：地球科学版，2010，40（5）：1194－1198.

Zhang Chong，Mao Zhi－qiang，Xiao Liang，et al.Comparation of Calculating Methods of Cation Exchange Capacity Qv Using Logging Data［J］.Journal of Jilin University：Earth Science Edition，2010，40（5）：1194－1198.

［2］ Guyod H.An Investigation of the Factors Affecting the SP in Soft Formations［C］／／Symposium Transaction of SPWLA.Houston：SPWLA，1964.

［3］ 王斌，范晓敏，陈启艳，等.用有限差分法模拟自然电位测井的侵入带影响［J］.测井技术，2008，32（2）：164－168.

Wang Bin，Fan Xiao－min，Chen Qi－yan，et al.Modeling Effect of Invaded Zone on SP Log with Finite Difference Method［J］.Well Logging Technology，2008，32（2）：164－168.

［4］ 潘克家，谭永基.复杂地层中自然电位测井的高效数值模拟［J］.石油地球物理勘探，2009，44（3）：371－376.

Pan Ke－jia，Tan Yong－ji.An Efficient Algorithm for Simulation of Spontaneous Potential Log in Complex Formations［J］.Oil Geophysical Prospecting，2009，44（3）：371－376.

［5］ 孔峰，谭永基.自然电位测井中的一个数值算法［J］.复旦学报：自然科学版，2010，49（4）：483－490.

Kong Feng，Tan Yong－ji.A Numerical Method for Spontaneous Potential Well－Logging［J］.Journal of Fudan University：Natural Science，2010，49（4）：483－490.

［6］ 汪功礼，张庚骥.数值计算的SP－3图版［J］.测井技术，1999，23（1）：24－28.

Wang Gong－li，Zhang Geng－ji.SP－3Charts by Numerical Method［J］.Well Logging Technology，1999，23（1）：24－28.

［7］ 李舟波.钻井地球物理勘探［M］.北京：地质出版社，2006.

Li Zhou－bo.Borehole Geophysical Exploration［M］.Beijing：Geological Publishing House，2006.

［8］ 张庚骥.电法测井［M］.北京：石油大学出版社，1996.

Zhang Geng－ji.Electrical Logging［M］.Beijing：Petroleum University of China Press，1996.

［9］ Dickey P A.Natural Potential in Sedimentary Rocks［C］／／Transactions of AIME.［S.l.］：AIME，1944.

［10］ 薛琴坊.场论［M］.北京：地质出版社，1978.

Xue Qin－fang.Field Theory［M］.Beijing：Geological Publishing House，1978.

［11］ Vengelishtien B Y.Study on Oil and Gas well Section by Spontuneous Potential Method［M］.Moscow：Geocenter Press，1966.

Distribution of Source in Numeric Modeling of Spontaneous Potential Log

Fan Xiao－min，Li Zhou－bo

College of GeoExploration Science and Technology，Jilin University，Changchun 130026，China

In order to facilitate efficient modeling of SP－log，and investigate the influences factors quantitatively，investigation on the stimulating source for SP，the electrical double layer（EDL）was performed.Through analyzing of the physical origin of spontaneous potential and the contribution of EDL to SP，it is clear that only the EDL at the borehole wall of shale layer，sand－shale boundary with invaded zone and that between invaded zone and virgin formation would contribute to the value of SP－log.In case only the anomalies of sand layer are concerned，to calculate the contribution of the EDL between invaded zone and virgin formation is sufficient.By analog of direct current electric field and static electric field，expression for the surface current density of EDL is deduced.SP－logs for different depth of invasion were calculated for media with uniform resistivity.The results show that the form of SP－log becomes flatter with the increasing depth of invasion，the amplitude of anomaly become smaller at the same time.

spontaneous potential logging；electric double layer；electrochemical EMF；influence of invasion depth

book=2012,ebook=565

P631.81

A

1671－5888（2012） 04－0895－05

2012－04－18

国家自然科学基金项目（40874057）；国家“863”计划项目（2009AA09A202－01－01）

范晓敏（1962－），男，教授，主要从事地球物理测井方法与应用研究，E－mail：fanxm＠jlu.edu.cn。