基于着色petri网的高速公路交通流建模与仿真

长安大学 信息工程学院 韩小龙

基于着色petri网的高速公路交通流建模与仿真

长安大学 信息工程学院 韩小龙

作为一种高级petri网，着色petri网是对经典petri网的拓展和延伸，其仿真工具CPN Tools支持功能强大的元语言（ML），扩展性比较强。

一、petri网的基本概念

1.经典petri网。经典petri网是由库所（place）、变迁（transition）和一组弧线（ares）组成的双向图。不同类型节点之间用弧线直接相连，同类型节点间则不能直接相连。本文，笔者用圆圈表示库所，用矩形形式表示变迁。经典petri网模型如图1所示。

图1 经典petri网模型

2.着色petri网。着色petri网通过不同的颜色对托肯进行分类，以实现系统的折叠和简化。着色petri网的颜色主要是针对托肯和库所设置的。

（1）通常把染色托肯分为几种类型，而把类型称为颜色。因此，可以把颜色看成是数据类型，对不同的属性的托肯赋以不同的颜色。在着色petri网中，一种颜色的托肯代表一类具有相同属性的元素；在经典petri网中，一个托肯只代表一个元素或资源。

（2）基本petri网的发射条件与着色petri网的托肯的发射条件是不相同的。在着色petri网中，在任意2个节点间的有向弧上，都表示一个相应的权值函数，每个权值函数明确地规定了相应的发射条件，包括变迁节点在其输人位置节点所应有的色点的颜色、变迁节点在完成发射后应清除的和应产生的色点的颜色等内容。

二、高速公路的路段模型

假设在某路段上设有出口和入口匝道。对该路段，以距离X为单位将该路段路段划分为N段，选取其中的i－1，i，i＋1段作为研究对象，而且i－1不是起始段，i－1也不是终点段。通常将q随道路坐标x连续变化的规律离散化，即把一条道路按照其实际和交通状况划分为若干段，使得在每一段内交通状态可近似成一的，每一段内车道数不变，至多有1个入口和出口。高速公路路段模型如图2所示。

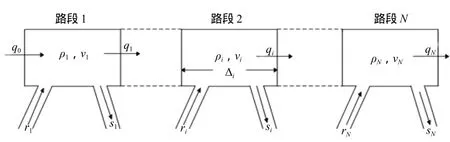
图2 高速公路路段模型

设第i路段内交通流量为qi，入口、出口匝道流量分别为ri，si，则

式（1）即为稳态流量模型，这是一个递推模型。只要知道起始端主线流量q0及各入口、出口匝道的流量，即可用式（1）计算出各段的流量qi（i＝1，2，…）。

三、CPN Tools建模

1.CPN Tools建模。根据高速公路路段的模型，建立交通流的CPN模型，如图3所示。

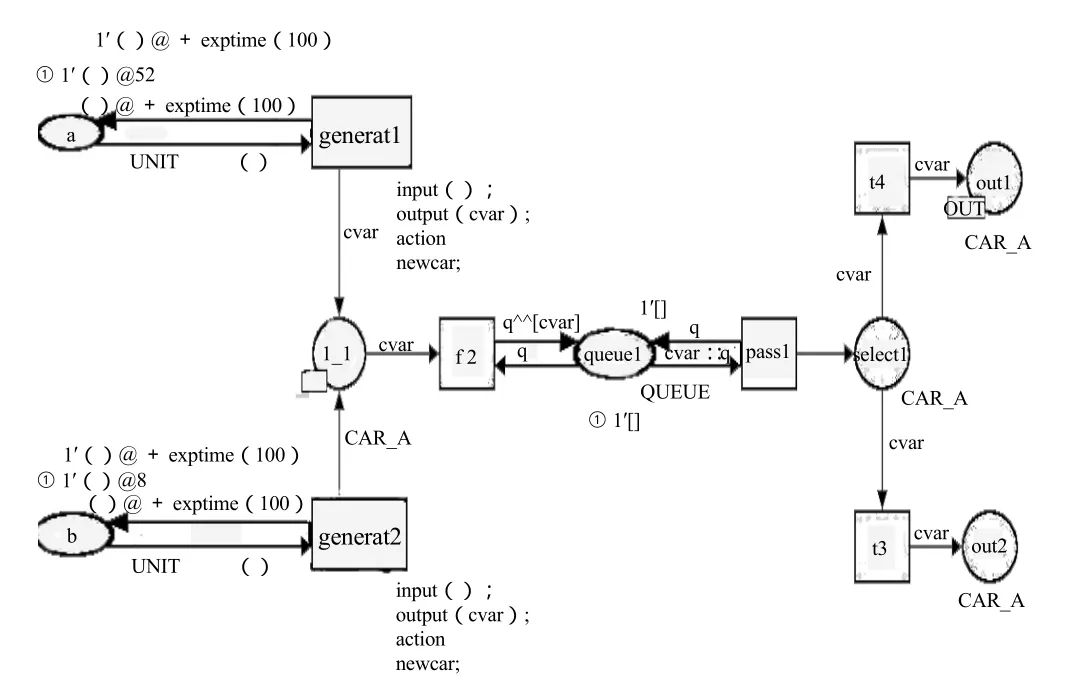
图3 高速公路路段交通流的CPN模型

库所a和变迁generate1为路段i的起始点，具有初始车流量，准备进入此段路口，而变迁generate1模拟交通流通过路口并且产生新的交通量。库所a的颜色集为UNIT（单元集）并且是时间集，在库所a上的token用于确定新的车流量何时产生，其token的时间标记将确定变迁generate1发生的时间，在库所a上初始标记是没有token的。

2.变迁generate1。变迁generate1是用于产生1个token放置在库所a中，对增加到库所a中的token的时间标签是由从变迁generate1到库所a上的时间标记@＋expTime(100）所创建的。expTime函数将从指数随机分布函数中返回1个值，来确保产生的token不总是在0时刻到达的。同理，库所b和generate2的作用与之相同，而库所b和generate2代表路段i的入口匝口的模型。

库所1–1为路段i的主干道和入口匝口的汇集点，变迁f2为汇合后的车流进入此路段的过程，并且进行相应的排队。库所queue1队伍形成后车流的状态，至变迁pass1即将驶离此路段，车辆离开队伍。库所select1则是出口匝口与进入下一路段的分离点，车辆再次选择行进方向。out1为通过主干道的车辆，out2通过出口匝口的车辆。CPN模型中元素的说明见表1。

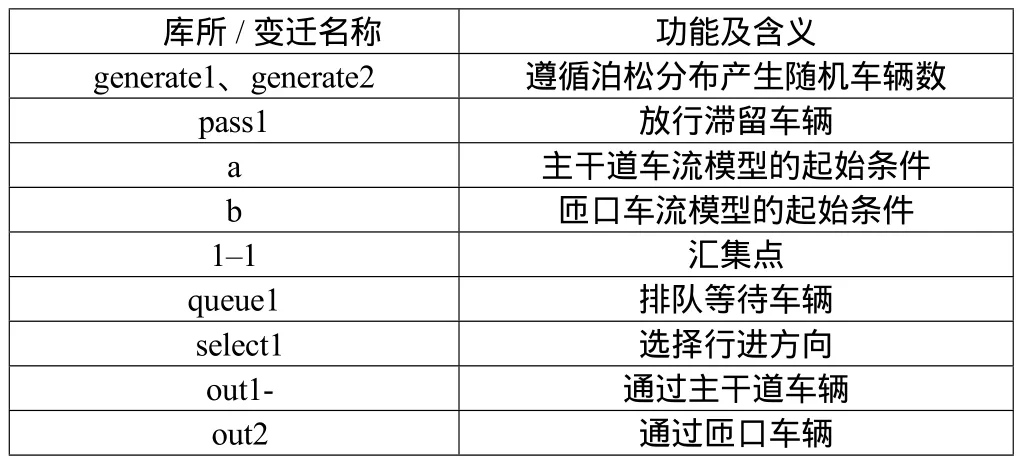
表1 CPN模型中元素的说明

全局声明如下：

colset UNIT ＝ unit timed；

colset INT ＝ int timed；

colset CarType＝ with A | B；

colset CAR_A＝ record cartype:CarType*CARNUM:INT*GT：INT；

var cvar:CAR_A；

colset QUEUE＝ list CAR_A；

var q:QUEUE；

fun Generate(）＝

let

val car＝ poisson（100.0）

in

car

end；

fun intTime（） ＝ IntInf.toInt （time(））；

fun nlength[]＝ 0|nlength（x::xs）＝ 1＋nlength xs；

fun expTime （mean: int） ＝

let

val realMean ＝ Real.fromInt mean

val rv ＝ exponential((1.0/realMean））

in

fl oor (rv＋0.5）

end；

fun newcar（） ＝ {cartype＝ CarType.ran（），

CARNUM ＝ Generate（），

GT ＝ intTime（） }

通过全局声明可编写相应的计算机程序，有利于实现对CPN Tools模型的分析。

book=45,ebook=90