一类热传导物理方程子域精细积分紧致Crank-Nicolson格式

潘金根

（安徽师范大学 继续教育学院，安徽 芜湖 241000）

一类热传导物理方程子域精细积分紧致Crank-Nicolson格式

潘金根

（安徽师范大学 继续教育学院，安徽 芜湖 241000）

本文在子域精细积分方法的基础上，针对一维空间中的热传导议程的模型的初边值问题，构造出一个含参数α的无条件稳定的高精度紧致Crank-Nicolson差分格式。数值实验结果表明，该格式的精度比以往各种格式的精度均高。同时，这种格式还是无条件稳定的，便于实际问题的计算。

热传导方程;子域精细积分;Crank-Nicolson格式;稳定性

1 引言

热传导是热传递三种基本方式之一，热传导实质是由大量物质的分子热运动互相撞击，而使能量从物体的高温部分传至低温部分，或由高温物体传给低温物体的过程．热传导方程（或称热方程）是描述一个区域内的温度如何随时间变化，支配热传导及其它扩散过程，诸如粒子扩散或神经细胞的动作电位等物理现象的一类重要物理模型，它的非线性的推广型式还可应用于影像分析，另外此类物理模型在工程技术等方面也都有着广泛的应用．因此,研究热传导物理方程的数值计算方法有重要的科学意义和应用价值．一维空间中的热传导方程模型为

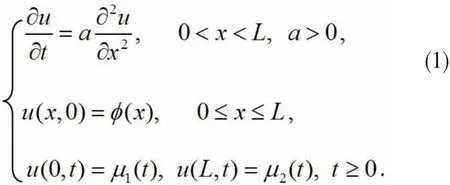
针对该类物理模型数值计算方法的一些已有文献，文[1]构造的高精度差分格式相应截断误差为O(τ2+h2),其中τ和h分别为时间和空间步长，文[2]和文 [3]的格式精度相对要高些,截断误差已达O（τ3+h4）,其中文[2]的格式为一族三层(特殊情况下为两层)双参数,绝对稳定的隐格式,文[3]的格式虽然精度较高，但是格式的稳定性要求太严格,必须满足0〈r〈1/2，且也为三层的格式.可见,对于上述模型的数值计算方法,关键是能否构造出一个稳定性好、精度高的差分格式.

钟万勰最初于1995年提出子域精细积分方法[4-6]来求解偏微分方程,其中文[6]的截断误差阶仅为O (τ+h2)．随后,赖永星[7-8]等提出了多点子域积分的方法．本文是在子域精细积分方法的基础上，针对模型(1)的初边值问题，构造出一个含参数α＞0(α〈〈τ)无条件稳定的高精度紧致Crank-Nicolson差分格式，精度比上述文献中给出的格式都高,其局部截断误差阶为O(ατ2+α2τ3+h4)．最后，所给数值例子的计算结果与理论分析完全一致．

2 子域精细积分Crank-Nicolson差分格式

2.1 紧致差分公式的推导

其中Dx,Tx与δx依次为关于x的一阶偏微分算子,位移算子与一阶中心差分算子,下面建立中心差分算子δx和微分算子Dx的关系式.由Taylor展开，可得

于是 Tx=exp(hDx).

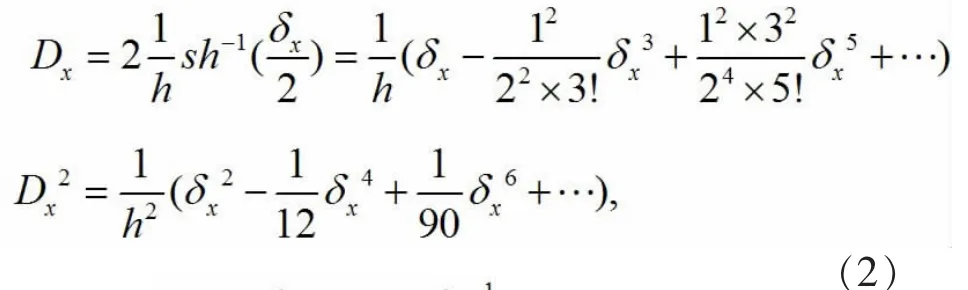
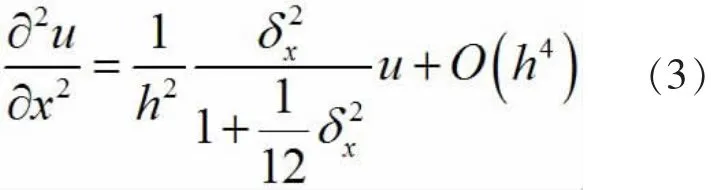
2.2 子域精细积分Crank-Nicolson差分格式的构造

,首先引入一个附加项αui（这里α＞0是参数）,加到方程（1）第一式的两端,得

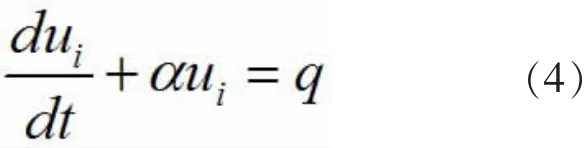
其中q=p+αui．如果令q为某一个常数，则利用常数变易法可解得方程（4）的通解

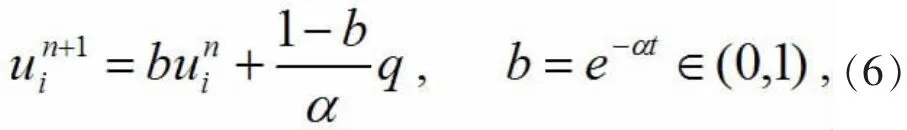
下面利用(3)式的四阶紧致差分公式，取将q代入（6），经整理得

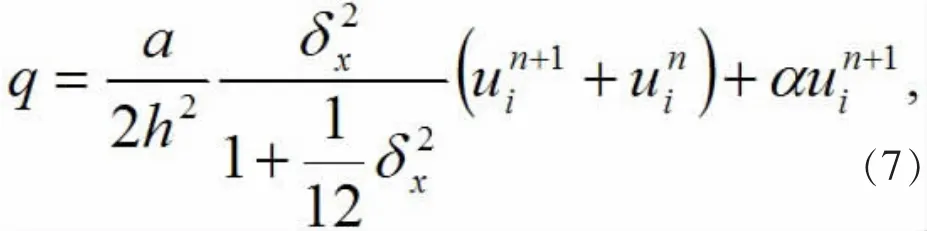
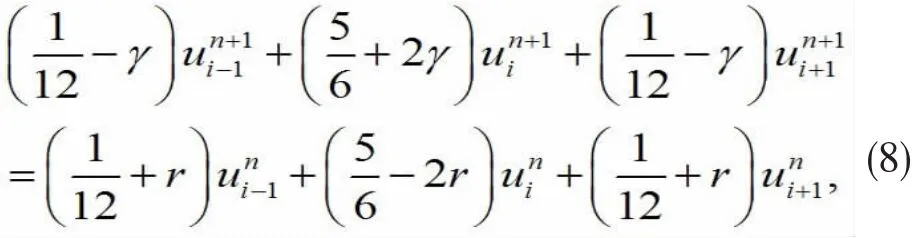
根据稳定性分析的Fourier方法对格式(8)进行稳定性分析，令代入(8)式经计算整理得增长因子

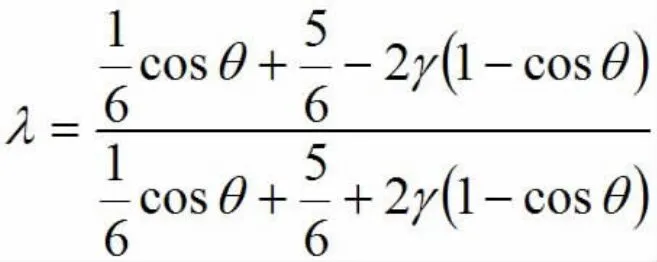
很显然｜λ｜≤1恒成立，所以隐格式(8)对任意参数α＞0是无条件稳定的．

此外，利用Taylor展开式容易求得格式(8)的在结点(xi,tn)处的局部截断误差为O(ατ2+α2τ3+h4)．可见本文格式(8)的精度比文[6]的精度O(τ+h2)要高.与马明书[3]提出的显式差分格式相比,当h固定不变,随着时间步长τ的增大,本文格式(8)所计算的精度也越高(因为α〈〈τ),且文[3]的格式是条件稳定的，必须满足0〈r〈1/2,这样的条件太严格,而本文所提出的格式是无条件稳定的．

3 数值实验

考虑问题模型(1),其实际算例见文献[3]，取α= 1,h=0.1来计算,其中r=τ/h2与文[3]和[6]的定义一致.利用本文格式(8)方法,取参数α=0.001进行计算,并与文[3]、文[6]的算法进行比较.数值结果如下表1和表2：

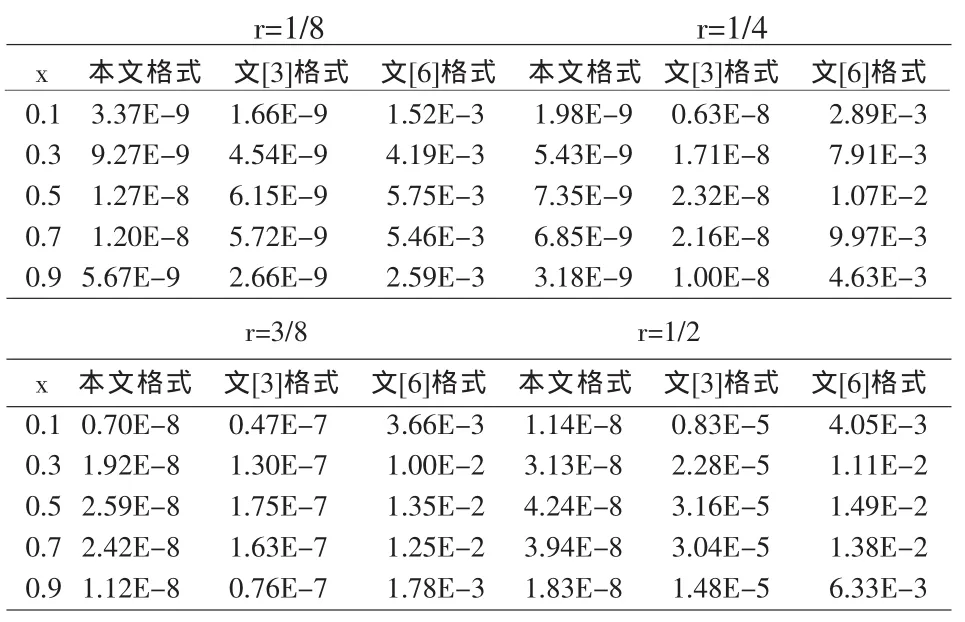
表1 本文的格式(8)与文[3]和文[6]格式数值解的绝对误差比较(n=200)

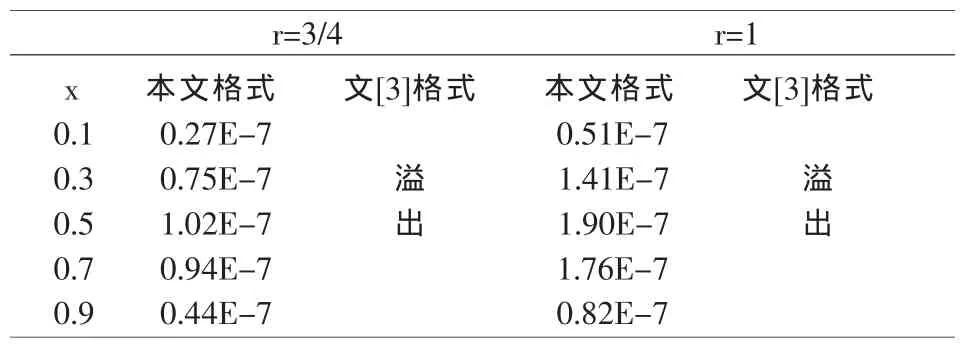
表2 本文的格式(8)与文[3]格式数值解的绝对误差比较(t=1)

4结论

从表1和表2中的数值结果可以看出,本文的格式明显比文[6]格式的精度高,当h固定不变,随着时间步长τ的增大,本文格式(8)的精度比文[3]格式的精度高(因为α〈〈τ,且文[3]格式的稳定性要求太严格,必须是文[3]中的格式(19)和格式(20)两个同时使用，才能使稳定性条件满足文[3]中的格式又是三层格式,在实际进行计算时,必须用其它办法求出第二层上各节点的函数值,这会给实际计算带来许多不便,不利于实际问题的计算.

[1]周顺兴.解抛物型偏微分方程的高精度差分格式[J].计算数学,1982,4(2):204-213.

[2]马明书.解抛物型方程的一族高精度差分格式[J].高等学校计算数学学报,1996,18(2):190-193.

[3]马明书.一维抛物型方程的一个新的高精度显式差分格式[J].数值计算与计算机应用,2001,22(2):156-160.

[4]钟万勰.子域精细积分及偏微分方程数值解[J].计算结构力学及其应用,1995,12(3):253-260.

[5]钟万勰.单点子域积分与差分[J].力学学报,1996,28(2):159-163.

[6]钟万勰.对差分法时程积分的反思 [J].应用数学与力学, 1995,16(8):663-668.

[7]赖永星，等.多点子域积分及计算格式的研究[J].机械强度, 2006,28(6):853-856.

[8]赖永星，等.单点子域积分与多点子域积分[J].计算力学学报,2006,23(3):373-376.

[责任编辑：桂传友]

O241

A

1674-1103(2012)03-0036－03

2012-02-16

安徽省农村骨干教师培训项目（WJMS2011-43）。

潘金根（1976-），男，安徽东至人，铜陵县第二中学教师，硕士，主要从事中学物理教学与研究。