Orlicz空间中广义Orlicz范数和Luxemburg范数的关系
段丽芬,庄彩彩
(通化师范学院数学学院,吉林通化 134002)
2006年,段丽芬和崔云安在Orlicz空间中引进了广义 Orlicz范数[1],并证明了它与 Orlicz范数[2]和Luxemburg范数[3]等价.本文进一步就由N-函数生成的Orlicz空间中定义的广义Orlicz范数和Luxemburg范数的关系问题加以讨论,得到一个严格不等式和一个重要的等价命题.
1 预备知识
映射M:R→[0,∞)称为Orlicz函数是指:M是偶的、非负连续凸函数且当且仅当u=0时M(u)=0.满足
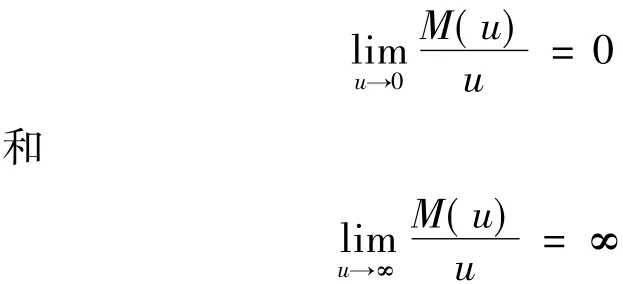
的Orlicz函数称为N-函数.
设M(u)、N(v)为一对互余的N-函数,(G,∑,μ)为一无原子测度空间,L0表示定义在G上的可测实函数全体.对任意x∈L0,我们称

为x(t)关于M的模.则Orlicz空间
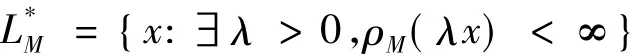
关于Orlicz范数:

Luxemburg范数:
‖x‖M=inf{λ > 0:ρM(x/λ) ≤1},
以及广义Orlicz范数:

均成为Banach空间.
引理1[4]设M是任意N-函数,则泛函

是Orlicz空间L*M的一个范数,且与‖x‖M等价.引理2[5]对任何b≥a > 0,集合

都为有界集的充要条件是M∈▽2.
引理3[6]设M∈△2,x∈L*M,则对任何ε >0都存在δ>0,当‖x‖M≥ε时,ρM(x)≥δ.
2 主要结果及证明

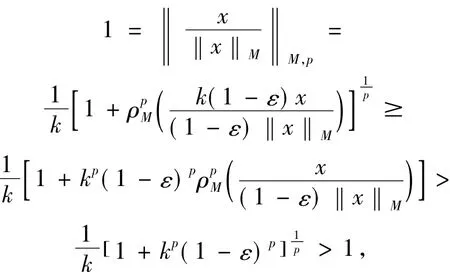
产生矛盾.
定理2 inf{‖x‖M,p:‖x‖M=1} > 1的充要条件是M∈△2∩▽2
证明 必要性.若M≠△2,存在αl↑∞ 使得

其中,F是一事先给定的正测度子集.选F的一个互不相交子集列{Fl}∞l=1使得
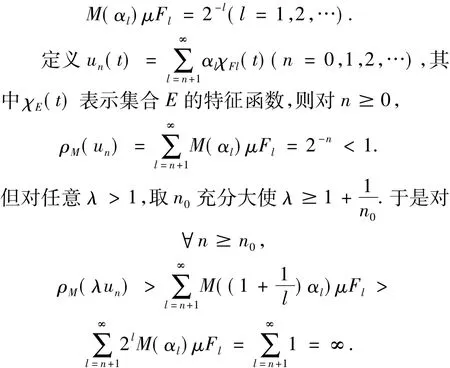


充分性.若 M∈ △2,则 ‖x‖M=1蕴涵着ρM(x)=1.因此,对x∈S(LM),如果k**x≥1,则

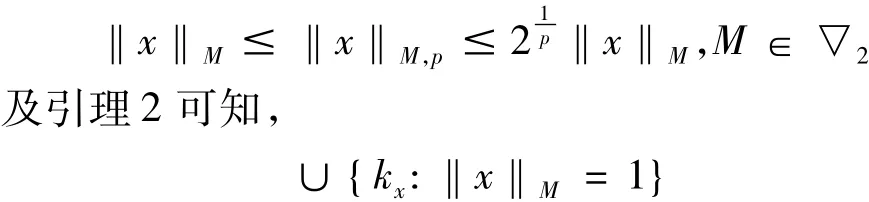
有界,设其为C.于是

由引理1证明过程:
定理 3 sup{‖x‖M:‖x‖M,p=1} < 1 当且仅当 inf{‖x‖M,p:‖x‖M=1} > 1.证明 假设

则对δ>0,-x1使得
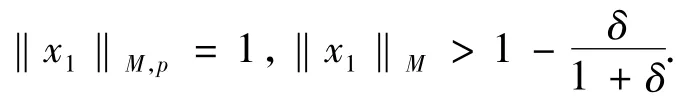

故 inf{‖x‖M,p:‖x‖M=1}=1.
这说明假设不成立.
另一方面,假设

则对0<δ<1,-x1使得
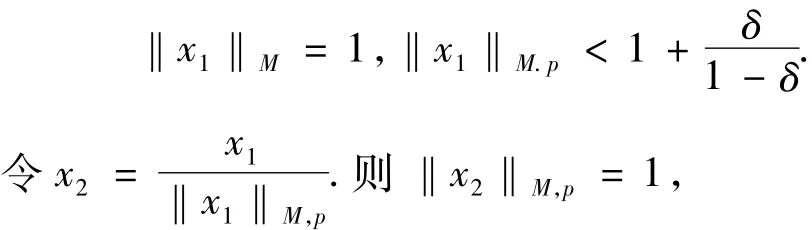

这说明假设不成立.
由定理2和定理3立即可得:
推论1 在Orlicz空间中,下面三个条件等价:

:
[1]段丽芬,崔云安.广义Orlicz范数和广义Luxemburg范数[J].兰州理工大学学报,2006,32(2):131-134.
[2]W.Orlicz.ber eine gewisse Klasse von Rumen vom Typus B[M].Poland:Bull.Acad.Polonaise A,1932:207 -220;Reprinted in:W.Orlicz.Collected Papers.Warszawa:PWN - Polish Scientific Publishers,1988:217 -230.
[3]W.A.J.Luxemburg.Banach function spaces[D].Delft Techn.Univ.,1955.
[4]段丽芬,崔云安.赋广义Orlicz范数的Orlicz空间的端点[J].浙江大学学报:理学版,2007,34(3):252-256.
[5]许晶,崔云安,庄彩彩.赋广义Orlicz范数的Orlicz空间中 的两个特征[J].通化师范学院学报,2010,31(12):14-15.
[6]CHEN S T,Geometry of Orlicz Spaces[M].Warszawa:Dissertations Math,1996:1 -204.

