含椭圆柱型空腔的声学覆盖层的吸声特性研究

商 超，魏英杰，张嘉钟，曹 伟

(哈尔滨工业大学航天学院，150001哈尔滨，shch1203@163.com)

声学覆盖层的主要用途是为降低水下结构的目标强度，它的基本结构形式是在阻尼材料中嵌入空气腔.对此类结构的吸声特性研究[1－2]从上世纪四五十年代就已开始，至今仍在不断深入探索.

对含空腔层的覆盖层主要是依靠空腔壁的径向运动和表面层类似鼓面的振动来消耗声能.Lane[3]通过不同穿孔层硬度对声学性能影响的实验认为，对应空腔上方的表面层振动是声能消耗的主要原因.但Gaunaurd[4]却认为表面层和穿孔层的相对刚度决定了覆盖层消耗声能的主要部位.汤渭霖等[5]运用柱面波展开法，对含周期排列短圆柱空腔的吸声覆盖层声学性能进行推导计算，研究结果发现，圆柱腔附近的轴对称波对覆盖层的低频消声特性起支配作用.赵宏刚等[6]利用多重散射理论系统讨论了含球腔覆盖层材料阻尼及背衬条件对其声学性能的影响.

而对于几何形状复杂的内部结构，覆盖层的声学特性无解析解.为能有效求解任意边值问题，需要采用数值方法，如有限单元法.Hennion[7－8]和Easwaran[9]采用有限单元法，研究了含双周期圆柱型空腔覆盖层的声学特性.谭洪波等[10]采用有限单元法研究了含圆柱形、球形空腔覆盖层的声学特性.

上述文献都是对含单个空腔且空腔截面均为圆形的覆盖层进行吸声性能研究.圆形柱[5]、圆球形[6]空腔易于用解析或近似的方法进行求解，但圆形属于椭圆形的1个特例，要优化覆盖层的吸声性能，必须对椭圆球和椭圆柱空腔进行研究.本文通过引入椭圆柱型空腔，研究了含单个空腔结构及混合型空腔结构覆盖层的吸声特性.

1 理论模型

1.1 声学流固耦合

为研究声学流固耦合问题，作如下假设:1)流体无流动;2)流体无粘性;3)流体是均质的;4)流体是可压缩的;5)相邻不同固体间连结完好.

设流固耦合界面为S，则在界面S处流体动量方程中的法向声压梯度与结构的法向加速度存在以下关系:

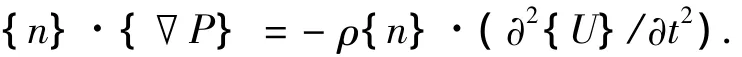
其中{U}为结构在界面S处的位移向量，{n}为界面S上由流体指向固体的单位法向量.

基于迦辽金方法可得到声学流固耦合问题的有限单元方程[11]如下:

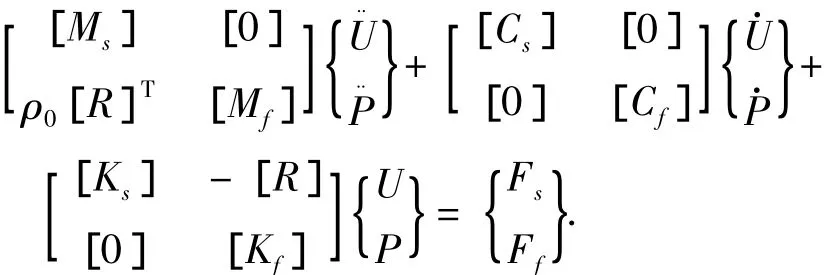
其中[R]为流固耦合矩阵.

1.2 粘弹性材料吸声和流体边界吸声

粘弹性材料(如橡胶)的弹性模量一般为复数形式.其中，弹性模量的实数部分代表材料的储能模量，虚数部分代表材料的损耗模量.此时，粘弹性材料的各弹性参数都应表示成复数形式，例如杨氏模量E的复数表示为

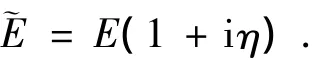
其中η为杨氏模量的损耗因子.由此，粘弹性材料的刚度矩阵[K]改写为如下的复刚度矩阵[˜K]:

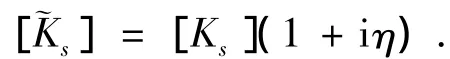
而复刚度矩阵[˜K]的虚数部分可以转化为阻尼矩阵[C]，即[Cs]=(η/ω)[Ks]，其中 ω 为圆频率.

流体阻尼矩阵[Cf]的表达式为

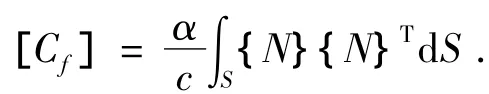
其中:α为该流体域外边界处的透声系数;c为流体中的声速;{N}为声压形函数.

取α的值为1时，声能在流体域外边界全透射，即为无反射边界，可用于模拟无限流场.

1.3 吸声系数

当平面声波从流体介质垂直入射到流固耦合界面S上时，声压的反射系数R可以用下式计算得到

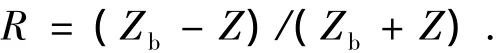
其中Z=ρc为流体介质的特征阻抗，Zb为粘弹性材料表面的机械阻抗.Zb通常为复数，计算式为Zb=p/v.其中p为流固耦合界面处流体侧节点上的压力，v为固体侧节点上垂直该界面的法向速度.而反射系数R与吸声系数α存在如下关系:

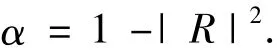
其中|R|为反射系数R的绝对值.

2 计算模型

计算所采用的模型如图1所示.其中，在钢板上敷设粘弹性覆盖层(嵌入双周期排列圆柱空腔的橡胶层)，覆盖层前为水层，钢板后为空气，可视为自由边界.平面声波从水中垂直入射到覆盖层表面上.

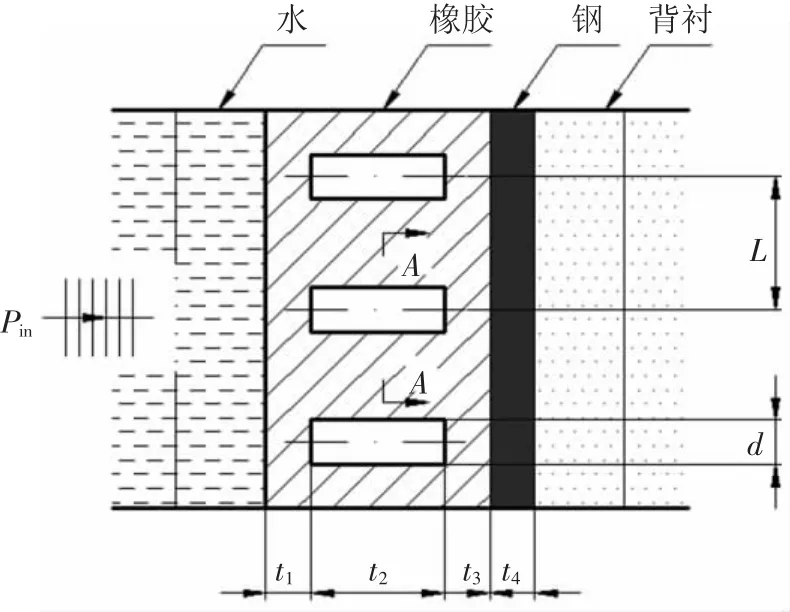
图1 模型结构示意

所采用的材料参数如表1所示，而橡胶的表面层、穿孔层、基层及钢板的厚度分别为t1=0.002 m，t2=0.046 m，t3=0.002 m和t4=0.005 m.

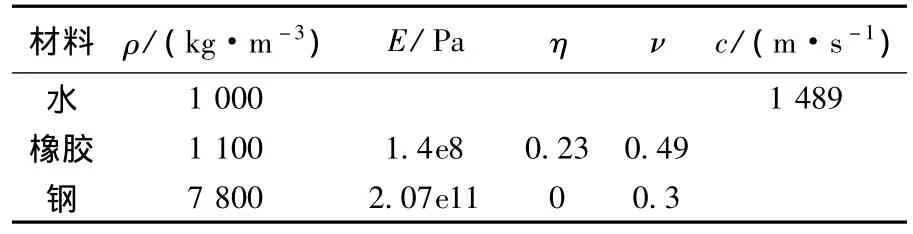
表1 材料参数

从文献[12]中知，具有相同穿孔率的不同结构的吸声性能是不一样的.4个小腔围绕中间1个大腔的结构具有更优良的吸声性能.数值计算时取用如图2所示的1个周期胞元.工况1为单圆柱型空腔结构，工况2为混合圆柱型空腔结构，工况3和工况4为两种混合型椭圆柱型空腔结构.胞元外部长度和宽度L=30 mm;大小空腔圆心横向中心间距L1=10 mm;算例均采用8节点6面体网格，网格最大尺寸为1.5 mm.

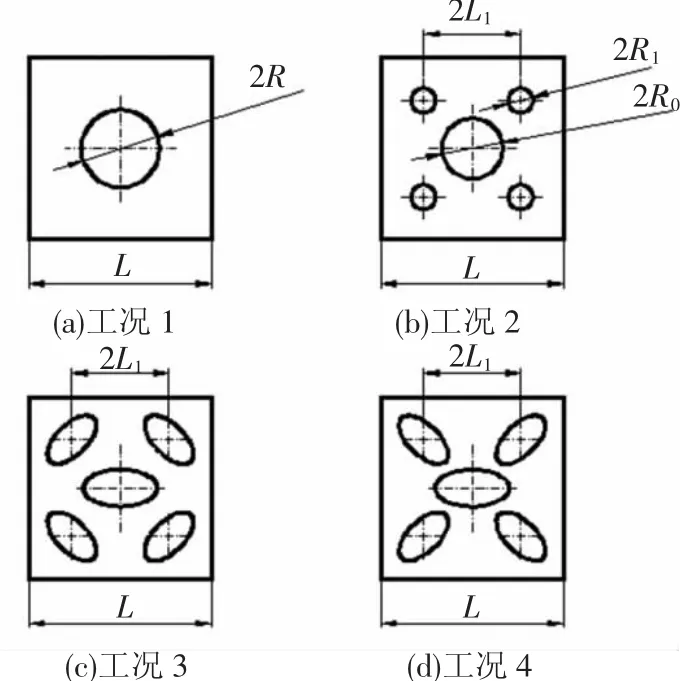
图2 A-A截面图

为改善声学覆盖层的吸声性能，优化圆柱型空腔声学结构，更加有效的利用覆盖层的空间，将圆柱型空腔更新为椭圆柱型空腔，对含空腔覆盖层的吸声机理做进一步研究.

3 仿真结果与分析

为验证计算方法的有效性，选取厚度为50 mm的均匀无腔覆盖层、5 mm厚的钢板、7.5 mm或75 mm厚的水层(用于模拟无限声学流场)，覆盖层吸声系数的计算结果如图3所示.其中，解析解采用文献[1]中的方法，但在材料的纵波声速计算公式中考虑泊松比的影响.使用公式如下:

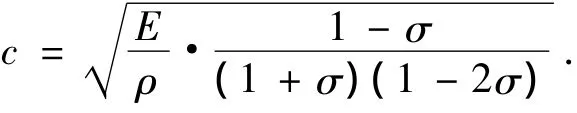
由图3可以看出，有限元结果与解析解能够非常好的吻合.并且无反射流体吸声边界的运用，使用较少的流体单元即可高精度的模拟无限声学流场，因而可以大大节约计算量，明显提高设计时的计算效率.在处理含空腔覆盖层时，只是在空腔内部增加了自由边界，流固耦合边界及无反射流体吸声边界均没有受到影响，有限单元法的准确性不受影响.

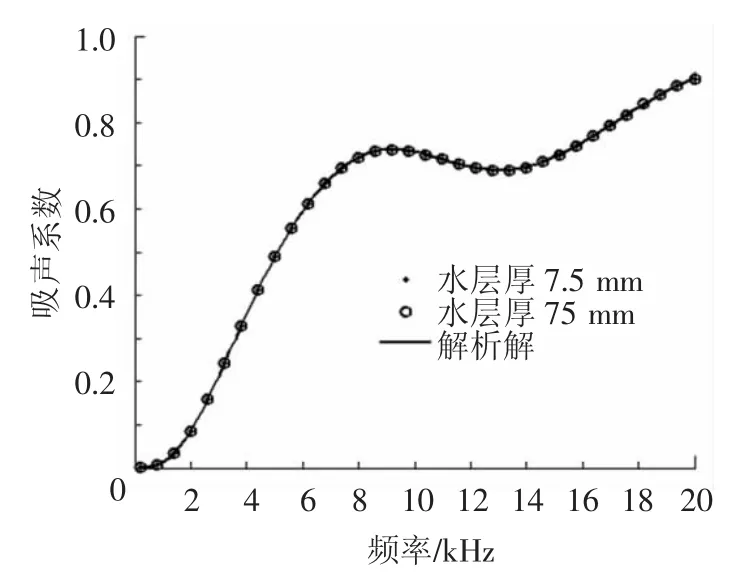
图3 无空腔时有限元结果与解析解的对比

图4为覆盖层中央含单个球形空腔时，有限元方法与多重散射法的对比.球半径为 r=0.011 22 m，与后面讨论的工况穿孔率相同.两种方法吻合较好，吸声系数最大差异不到0.015，可以接受，这同时也证明了两种方法的准确性.从图中可以看出，含单个球形空腔覆盖层的中高频吸声效果一般.

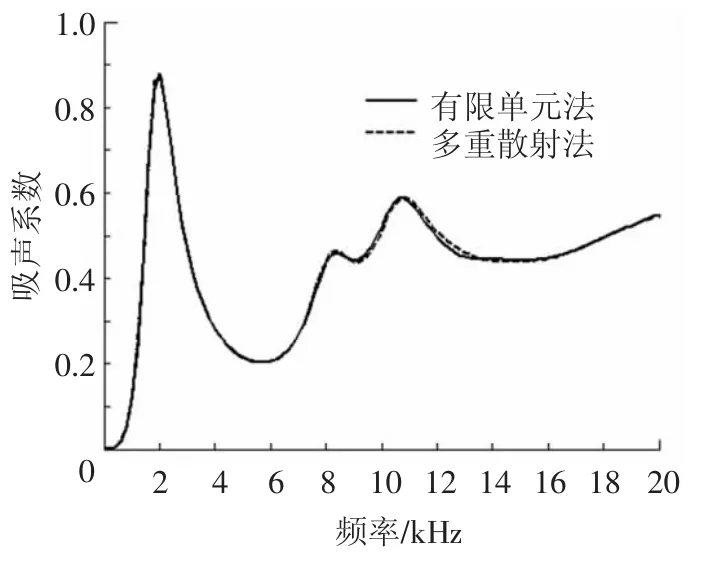
图4 含空腔时有限元解与多重散射理论解的对比

图5为相同穿孔率下，单圆柱型空腔结构与单椭圆型空腔结构的吸声系数曲线的对比.其中R为圆的半径，r为椭圆的扁率(椭圆的长短轴长度差 /长轴长度).从图中可见，随着椭圆扁率的增大，吸声系数曲线非常明显地向低频方向移动，且吸声峰变窄变高.这说明在穿孔率不变的情况下，含较扁空腔的结构能够降低声学覆盖层的谐振频率.

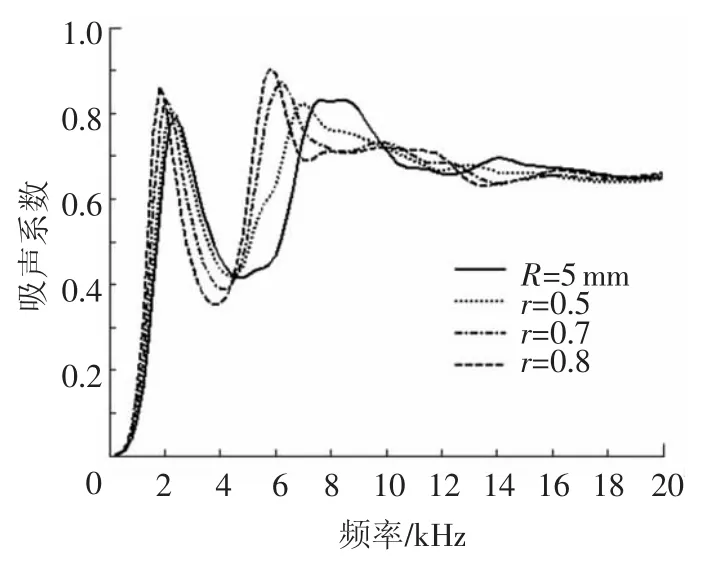
图5 相同穿孔率下空腔截面形状对吸声性能的影响

图6为4种工况在相同穿孔率下的吸声性能对比.在第一阶吸声峰前，各工况的吸声性能相近，其中单空腔结构(工况1)的第一吸声峰值略高;但之后混合型空腔结构的吸声性能相对单空腔结构有明显改进，在4～20 kHz中的大部分频段里，吸声系数提高0.1以上，最多可提高0.22.椭圆柱混合型空腔结构(工况3、4，扁率为0.5)相对圆柱混合型空腔结构(工况2)，吸声曲线向低频方向移动，第一吸声峰值增大，第二吸声峰值减小.工况4与工况3的吸声性能一直相近，但在9 kHz后出现明显差别，工况4的表现更加平稳.

图7和图8分别为相同穿孔率不同扁率下，工况3和工况4与工况2的吸声性能对比.随着椭圆扁率的增大，吸声系数曲线非常明显地向低频方向移动，且第一吸声峰变窄变高，第二吸声峰值逐渐变低.其中，工况4对扁率的影响更为敏感，且在高频段的震荡更趋平稳.三种工况在15 kHz以后的吸声表现趋于一致.

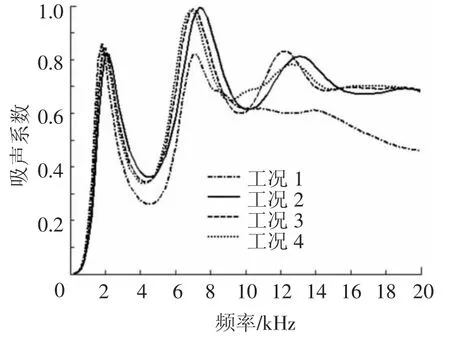
图6 相同穿孔率下不同空腔分布对吸声性能的影响

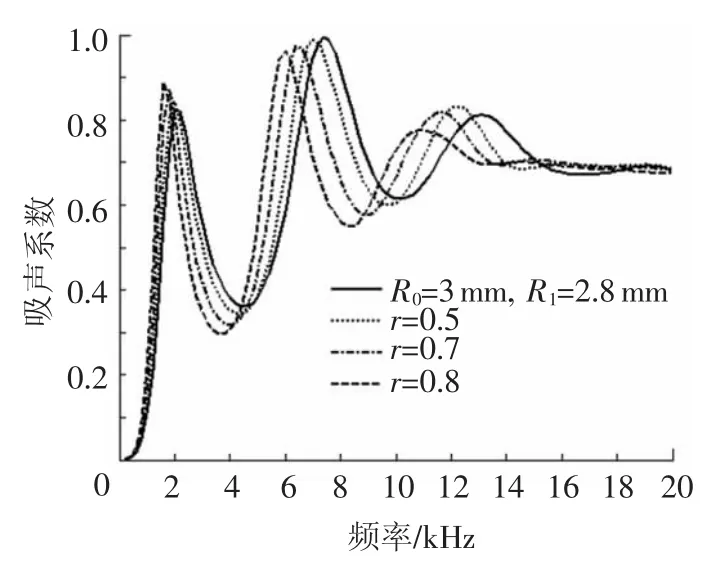
图7 相同穿孔率下不同扁率吸声性能的影响(工况2、3)

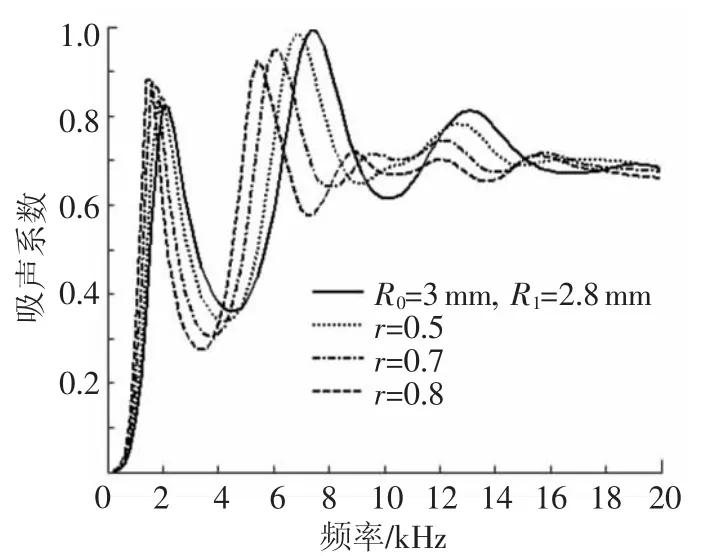
图8 相同穿孔率下不同扁率吸声性能的影响(工况2、4)

4 结论

本文基于有限单元法研究了以钢板和空气为背衬的含椭圆柱型空腔的声学覆盖层的吸声特性，并得到以下结论:

1)用有限单元法求解粘弹性材料覆盖层的吸声特性，能与解析解和多重散射理论解相吻合，证明了方法的准确性.

2)在穿孔率不变的情况下，含较扁空腔的结构能够降低声学覆盖层的谐振频率，且扁率越大，谐振频率越低，这符合覆盖层消声频率向低频方向发展的要求，研究椭圆柱形空腔是十分必要的.

3)在穿孔率不变的情况下，随扁率增大，第一吸声峰变窄变高，单空腔结构的第二吸声峰变窄变高，混合型空腔结构的第二吸声峰变窄变低;

4)在第一阶吸声频率峰值后，含混合型空腔结构的覆盖层在整个频段上的吸声效果明显优于含单个空腔结构的覆盖层，这符合覆盖层消声频率向宽频方向发展的要求.

5)在相同空腔分布和穿孔率的情况下，空腔截面形状变化，会影响覆盖层对中低频声波的吸收，但对高于15 kHz的声波的吸收影响不大.这说明含空腔结构的覆盖层的吸声机制是以谐振吸声为主.

[1]何祚镛，王曼.水下均匀复合结构吸声的理论研究[J].应用声学，1996，15(5):6－11.

[2]何祚镛，王曼.水下非均匀复合结构吸声的理论研究[J].应用声学，1996，15(5):12－19.

[3]LANE R.Absorption mechanisms for waterborne sound in Alberich anechoic layers[J].Ultrasonics，1981，19(1):28－30.

[4]GAUNAURD G C.Comments on‘Absorption mechanisms for waterborne sound in Alberich anechoic layers’[J].Ultrasonies，1985，23(2):90 －91.

[5]汤渭霖，何世平，范军.含圆柱形空腔吸声覆盖层的二维理论[J].声学学报，2005，30(4):289－295.

[6]赵宏刚，刘耀宗，温激鸿，等.含有周期球腔的粘弹性覆盖层消声性能分析[J].物理学报，2007，56(8)，4700－4707.

[7]HENNION A C，BOSSUT R，DECARPIGNY J N.Analysis of the scattering of a plane acoustic wave by a periodic elastic structure using the finite element method:application to compliant tube gratings[J].J Acoust Soc Am，1990，87(5):1861－1870.

[8]HENNION A C，DECARPIGNY J N.Analysis of the scattering of a plane wave by a doubly periodic structure using the finite element method:Application to Alberich anechoic coatings[J].J Acoust Soc Am，1991，90(6):3356－3367.

[9]EASWARAN V，MUNJAL M L.Analysis of reflection characteristics of a normal incidence plane wave on resonant sound absorbers:A finite element approach[J].J Acoust Soc Am，1993，93(3):1308－1318.

[10]谭洪波，赵洪，徐海亭.有限元法分析空腔周期分布粘弹性层的声特性[J].声学学报，2003，28(3):277－282.

[11]商超，魏英杰，张嘉钟，等.基于有限元法的 Alberich型覆盖层吸声特性研究[J].船舶力学，2011，15(4):443 －448.

[12]王勖成.有限单元法[M].北京:清华大学出版社，2003:523－531.