基于K-Medoids聚类的多传感器航迹关联算法

徐 丽，马培军，苏小红

(1.哈尔滨工业大学计算机科学与技术学院，150001哈尔滨，xuli－hit@126.com;2.哈尔滨工程大学计算机科学与技术学院，150001哈尔滨)

航迹融合必须以航迹关联为前提，因此关联判定的准确性将直接影响到整个航迹融合系统的性能.航迹关联备受国内外学者关注，一直是研究的热点问题之一.Ashraf M.Aziz[1]提出了一种基于模糊均值聚类的航迹融合方法来解决分布式多传感器多目标多属性重叠覆盖场景中的航迹关联和融合问题.Baoguo Tian等[2]将航迹关联问题转化成多维分配问题进行求解.Songhwai Oh等[3]用马尔科夫链蒙特卡洛数据关联算法较好地解决了目标密集环境下的航迹关联问题.Huang Youpeng等[4]提出了一种基于灰色关联分析的航迹关联算法，有效地实现了异构传感器的航迹关联.Kusha Panta等[5]提出了混合高斯概率假设密度滤波的航迹关联.Mei Duan等[6]提出了基于神经网络的航迹关联算法.这些算法的提出提高了多传感器航迹融合系统的效率.近年来，还有很多学者从其他角度研究了航迹关联问题.Donald E.Maurer[7]对关联的信息进行处理，提高了整个系统的效率.Lance M.Kaplan等[8]提出了关联多条航迹的代价函数.Dimitri J.Papageorgiou 等[9]扩展了最佳偏差关联假设和相应的偏差关联似然函数，使其更适合系统级航迹歧义管理.这些成果很大程度上促进了航迹关联问题的研究.特别是，文献[10]根据数据列因素之间发展态势的相似或相异程度来衡量航迹间接近的程度，首次用模式识别的方法解决了航迹关联问题，为求解航迹关联问题探索了一条新的途径.

本文提出了一种新的基于K-Medoids聚类的航迹关联算法.该算法采用局部航迹与系统航迹关联的策略，大大降低了需要关联的航迹对数量，从而提高了关联算法的效率.

1 系统描述

假设M个传感器观测杂波中的T个目标，在固定时间间隔内获取观测，每个观测都由几个量测组成，共观测n步.

设Xi(k)(1≤i≤T)为第k个测量时刻目标i的状态向量，假设输入项为零，则目标运动模型为

式中:Xi(k+1)为k+1时刻目标i的状态向量;F(k)为状态转移矩阵;G(k)为输入控制矩阵;ui(k)为加速度输入矩阵;vi(k)为离散时间白噪声序列，满足

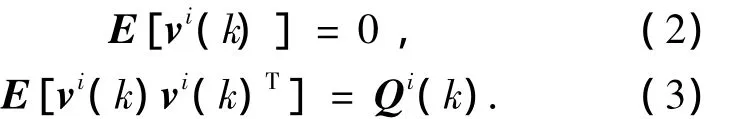
测量方程可表示为

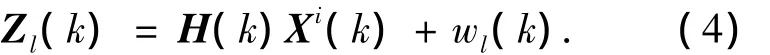
式中:wl(k)为零均值，方差为Rl(k)的Gauss观测噪声;H(k)是观测矩阵.

2 基于K-Medoids聚类的航迹关联算法

在分布式结构的航迹融合系统中，每个传感器都独立地处理它的局部量测，产生局部航迹并送至融合中心，融合中心根据各传感器的航迹数据完成航迹关联和航迹状态估计融合，形成全局估计.航迹关联的工作就是将来自不同传感器的航迹进行分组，使得同一组的航迹代表同一个目标.而聚类是将要处理的对象分成若干个类，使得同一类的对象尽量相似，不同类的对象尽量相异.二者都可用于发现隐藏在数据背后的分组和数据分布信息.实际上，二者的目标和作用是一致的.通过上述分析，可以从一个新的角度重新理解航迹关联问题.

2.1 关联策略

K-Medoids聚类算法属于划分方法中的一种常用的聚类算法，具有较高的准确性.因为Medoids不容易被极端数据影响，当存在噪声和孤立点数据时，K-Medoids算法依然很健壮，适合数据比较密集的数据集.然而，K-Medoids算法也存在一些缺陷:1)初始化敏感;2)聚类结果多样化;3)在进行Medoids轮换时需遍历所有非Medoids，执行代价较高.

由于在分布式多传感器航迹融合系统的实际应用中，所使用的传感器和每个传感器所扫描的目标数量都很多，如果对所有来自不同传感器的航迹都进行两两关联及融合处理，那将会给系统带来沉重的负担.因此，本文采用将局部航迹与系统航迹进行关联的策略，指定每条系统航迹作为一个固定的Mediod，这样就避免了K-Medoids算法初始化的随机性，也避免了Medoids轮换的沉重代价.而这种策略，本身就大大降低了需要关联的航迹对数量，使系统的效率得到了很大程度的提高.另外，由于来自同一传感器的航迹都是由不同目标形成的，所以一条系统航迹最多只能与来自某个传感器的一条局部航迹关联成功;又由于每条系统航迹都源于不同的目标，所以来自一个传感器的某条局部航迹最多只能与一条系统航迹关联成功，因此算法将根据规则最多为一条局部航迹找到一条系统航迹与其关联，这样避免了聚类结果的多样性.

2.2 算法描述

Step1 确定Mediods.

设系统航迹和来自传感器l的局部航迹的航迹号集合分别为

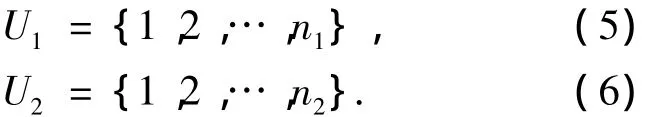
即系统航迹集合中有n1条系统航迹，来自传感器l的局部航迹集合中有n2条局部航迹.

指定每条系统航迹作为一个Mediod，每个Medoid标识一个类，共n1个类.记为

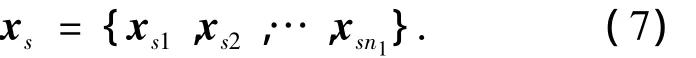
传感器l的n2条局部航迹记为

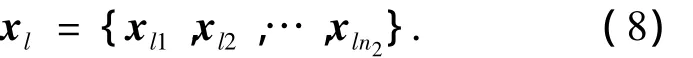
Step2 计算两条航迹k时刻点迹的距离.

假设航迹i在k时刻经过标准化处理后的状态向量为

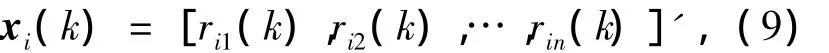
相应的分辨率为

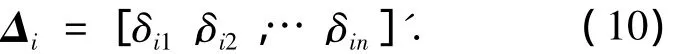
式中:rk为航迹的特征;n为特征的个数;δk为每个特征相对应的分辨率.

利用无穷范数定义航迹i和航迹j在k时刻的点迹距离为

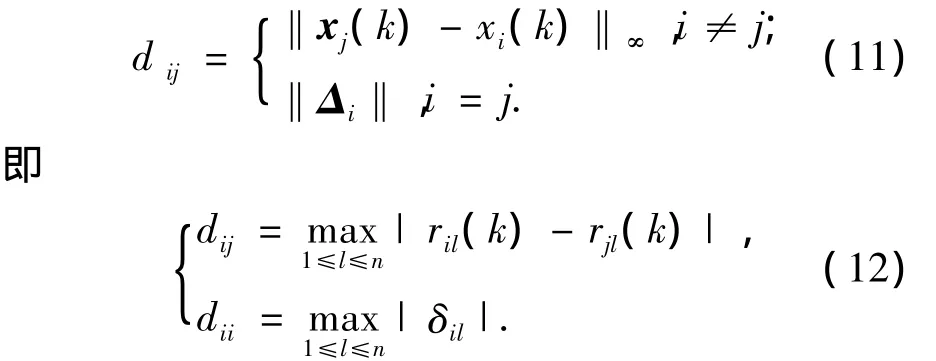
进而，利用平均值法计算出描述两条航迹接近程度的近似距离，即

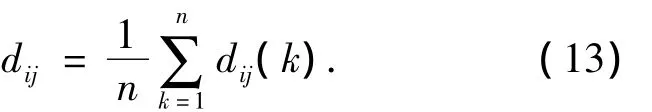
Step 3 构造来自传感器l的局部航迹与Medoids的距离矩阵.

当计算出两条航迹的近似距离之后，可以构造出来自传感器l的局部航迹与Medoids的距离矩阵为

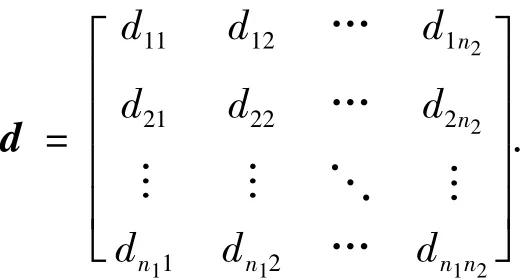
Step 4 关联准则.

根据与Medoids距离最近的原则，即 di=且di＜dii.将待关联的局部航迹分到各个类中去，即指派每个局部航迹给离它最近的Medoid所代表的类.当一个Medoid与多条局部航迹距离相等且都为最小时，由于一条系统航迹最多只能与来自某个传感器的一条局部航迹来自同一个目标，且目标位置是关联判决中一个较为关键的属性，算法将选择与该Medoid平均位置无穷范数最小的局部航迹作为最终的关联航迹.当di＞dii时，说明该局部航迹不与任何Medoids关联，这时指定此局部航迹作为一个新的Medoid.这样就给出了系统航迹与来自传感器l的局部航迹的关联判决.

Step 5 多义性处理.

一条来自某个传感器的局部航迹最多只能与一条系统航迹关联.因此当一条局部航迹与多条系统航迹关联成功时，需要进行多义性处理.在这种情况下算法选择与该局部航迹距离最小的系统航迹为关联航迹，如果与该局部航迹距离最小的系统航迹依旧有多条，则算法选取其中平均位置无穷范数最小的那条系统航迹作为最终与该局部航迹关联的航迹.经过多义性处理后，每条局部航迹就最多只能与一条系统航迹关联成功.

经航迹关联后，将关联成功的航迹对进行航迹状态估计融合.

3 实验分析

3.1 初始设置

为了讨论问题方便，假设送至融合中心的所有状态估计都在相同的坐标系里，并且各传感器同步采样，数据的传输延迟时间为0.仿真实验采用两个传感器同时观测目标，模拟目标在三维空间中做变速机动运动.为了验证算法的性能，采用Monte Carlo方法对本文算法进行50次仿真.仿真考虑两种情况:1)模拟中等密度目标环境，开始进入公共区的目标为60批;2)模拟密集目标环境，开始进入公共区的目标为120批.图1和图2分别给出了在公共观测区域60批目标和120批目标的运动轨迹.

图1 60批目标航迹图

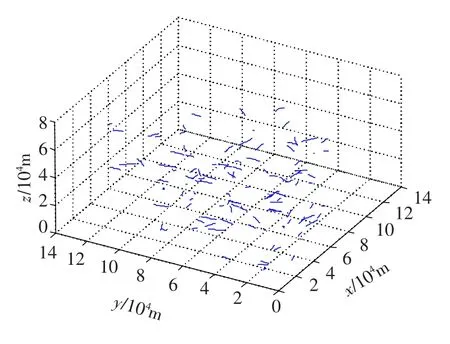
图2 120批目标航迹图

3.2 实验结果与分析

图3与图4分别给出了在60批目标下分别采用最近邻域法(NN)、模糊C均值法(FCM)及本文算法(K-Mediods)，仿真50次后的平均正确关联率(Pc)曲线和平均错误关联率(Pe)曲线.

图5与图6分别给出了在120批目标下分别采用最近邻域法(NN)、模糊C均值法(FCM)及本文算法(K-Mediods)，仿真50次后的平均正确关联率(Pc)曲线和平均错误关联率(Pe)曲线.

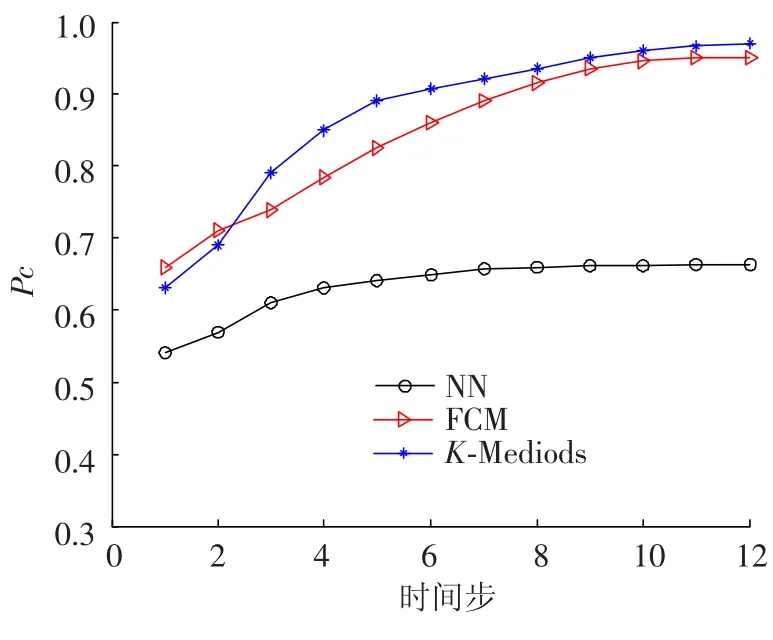
图3 60批目标下正确关联率对比

图4 60批目标下错误关联率对比

图5 120批目标下正确关联率对比

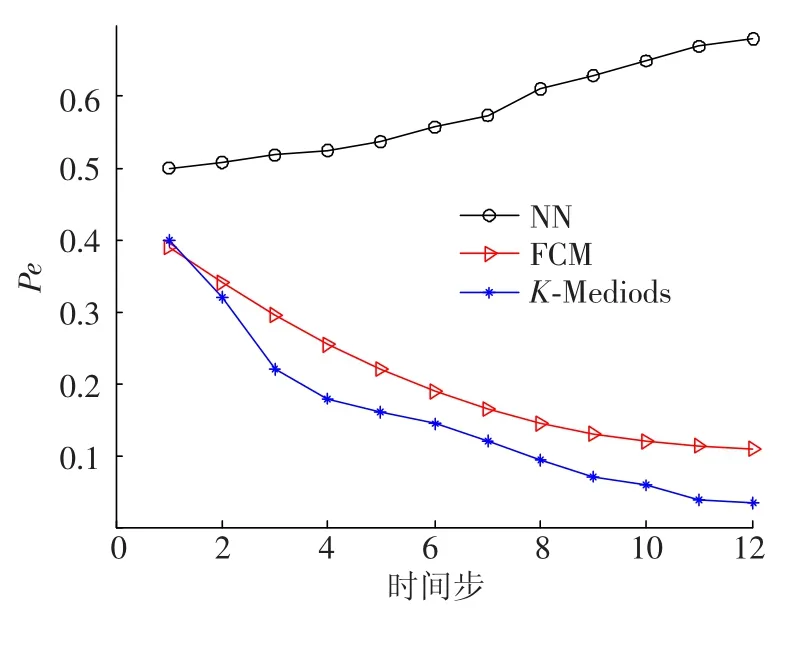
图6 120批目标下错误关联率对比

表1统计了采用最近邻域法(NN)、模糊C均值(FCM)及本文算法(K-Mediods)对各目标进行航迹关联的平均计算时间.

表1 关联时间对比 s

从实验结果可以看出最近邻域法速度很快，但是正确关联率最低.该算法不适合中等密度和密集目标环境，特别在密集目标环境下，随着关联时间步的增加，其正确关联率逐步下降.模糊C均值法的正确关联率较高，在中等密度目标环境下与K-Mediods方法相当，但在密集目标环境下，其正确关联率与K-Mediods方法的差距变大，且效率较低.本文算法K-Mediods方法的正确关联率在中等密度和密集目标环境下都为最高，在目标密集环境下，仍然可以达到较高的正确关联率.

4 结论

1)基于K-Medoids聚类的航迹关联算法采用局部航迹与系统航迹关联的策略，减少了需要关联的航迹对数量，缩短了关联时间，提高了系统的效率;系统航迹被指定为 Mediods，使得用K-Mediods聚类方法求解航迹关联问题克服了该方法本身的缺陷.

2)通过用无穷范数量化两条航迹在采样点的点迹距离得到了两条航迹的近似距离，从而确定了来自某个传感器的局部航迹与系统航迹的关联矩阵，使得关联判决能考虑当前和历史航迹，提高了正确关联率.

3)模拟实验表明该算法在目标密集环境下，以较小的计算开销达到了较高的精度.由于K-Medoids聚类算法本身的优越性，算法在存在噪声和离群点时，具有很强的健壮性.

[1]AZIZ A M.Fuzzy track-to-track association and track fusion approach in distributed multisensor—multitarget multiple-attribute environment[J].Signal Processing，2007，87(6):1474－1492.

[2]TIAN B G，ZHANG J P，YANG S L.Algorithm of fuzzy track correlation in multisensor system based on neural network[C]//Proceedings of the 8th International Conference on Signal Processing.Washington，DC:IEEE Computer Society，2006:316－319.

[3]OH S，RUSSELL S，SHANKAR S.Markov chain Monte Carlo data association for multi-target tracking[J].IEEE Transactions on Automatic Control， 2009，54(3):481－497.

[4]HUANG Y P，ZHOU Y F，ZHANG H B.Heterogeneous sensors track-to-track correlation algorithm based on gray correlative degree[C]//Proceedings of the 2008 International Symposium on Computer Science and Computational Technology.Washington，DC:IEEE Computer Society，2008:104－108.

[5]PANTA K，CLARK D E，VO B.Data ASsociation and track management for the gaussian mixture probability hypothesis density filter[J].IEEE Transactions on Aerospace and Electronic Systems，2009，45(3):1003 －1016.

[6]DUAN M，LIU J H.Track correlation algorithm based on neural network[C]//Proceedings of the 2009 Second International Symposium on Computational Intelligence and Design.Washington，DC:IEEE Computer Society，2009:181－185.

[7]MAURER D E.Information handover for track-to-track correlation[J].Information Fusion，2003，4(4):281 －295.

[8]KAPLAN L M，BAR-SHALOM Y，BLAIR W D.Assignment costs for multiple sensor track-to-track association[J].IEEE Transactions on Aerospace and Electronic Systems，2008，44(2):655－677.

[9]PAPAGEORGIOU D J，HOLENDER M.Track-to-track association and ambiguity management in the presence of sensor bias[C]//Proceedings of the 12th International Conference on Information Fusion.Washington，DC:IEEE Computer Society，2009:2012 －2019.

[10]衣晓，关欣，何友.分布式多目标跟踪系统的灰色航迹关联模型[J].信号处理，2005，21(6):653－655，662.