多区域GRECO虚拟屏幕算法分析电大尺寸目标RCS

赵玉磊,童创明,鞠智芹

(空军工程大学 导弹学院,陕西 三原 713800)

1 引 言

随着现代军事技术的迅猛发展,对飞行器和地面目标隐身特性的要求越来越高,作为衡量目标隐身能力以及进行雷达目标识别研究的重要参数,雷达散射截面积(Radar Cross Section,RCS)一直受到各国高度的关注和重视。雷达散射截面的研究方法分为低频方法和高频方法,低频方法有有限元法(FEM)[1]、时域有限差分法(FDTD)[2]以及矩量法(MOM)[3]。有学者将快速多级子方法(FMM)和多层快速多级子方法(MLFMM)引入矩量法(MOM)[4-6],从而使得低频方法分析较大电尺寸目标电磁散射特性成为可能。然而,受限于计算机的内存,使得低频方法仍具有局限性,不能计算电尺寸特别大的目标,此时就必须借助高频方法。常用的高频方法可以归纳为两类:一类基于几何光学,包括几何光学法(GO)、几何绕射理论(GTD)以及在GTD基础上发展的一致性绕射理论(UTD)等[7-9];另一类基于波前光学,包括物理光学(PO)、物理绕射理论(PTD)、等效电磁流法(MEC)[10-12]以及基于物理光学法的图形电磁计算方法(GRECO)[13]。低频方法精确性高但是计算速度慢,无法解决电尺寸特别大目标的雷达散射截面。高频方法优点是简单明晰,计算速度快,甚至可以实时显示计算结果。

图形电磁计算方法(Graphical Electromagnetic Computing,GRECO)是20世纪90年代新发展起来的一种方法,是一种计算机图形学与高频RCS计算相结合的方法,具有存储量小、计算精度高、运算速度快、实时性好等优点。GRECO方法基本原理:把目标成像在屏幕上,利用计算机的硬件加速器自动完成消隐,避免了费时的人工消隐;通过读取计算机的深度缓存区中的信息,可以获得可视面上任一点的深度值;物体的可视面以屏幕像素为单位自动完成剖分。三角面片建造的模型具有精确且易于操作等优点,是非常重要的一种建模方法,如何方便地识别出由三角面元组成的复杂模型相对于观察点可见的三角面片是研究目标电磁散射特性的基础。基于GRECO可很方便地识别出相对于观察点可见的三角面片。

当目标的尺寸很大时,屏幕上每一个像素对应的实际空间的尺寸超过一个三角面元的尺寸,传统的GRECO方法将无法识别出相对于观察点可见的三角面片,而多区域方法可以很好地克服这个问题。多区域方法就是将目标成像划分为多个部分分别在计算机屏幕上独立显示,相当于增大了屏幕的分辨率,使得像素对应的实际空间尺寸远远小于三角面元的尺寸,这样就可以识别出可见三角面元。然而多区域方法存在另一个问题:区域间结合部分的三角面元可能横跨两个或多个区域,使得这部分三角面元无法被识别出来,导致计算结果不准确。对于上述方法存在的不足,本文提出了多区域GRECO虚拟屏幕算法,将多区域方法中划分的各个区域投影到一个虚拟的屏幕上,基于虚拟屏幕就可以识别出所有可见的三角面元。

2 理论基础

2.1 RCS的计算公式

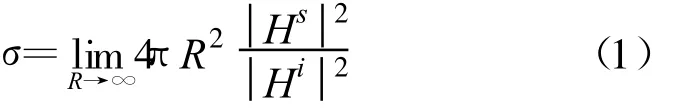
式中,σ为RCS,R为观察点到目标散射中心的距离,Hs为观察点处散射磁场,Hi为目标散射中心处入射磁场。在此公式中,R、Hi为已知,只需要求出Hs即可求得σ。

2.2 基于PO法计算散射磁场

对于完纯导体,基于物理光学法的三点假设,散射磁场的计算公式为

基于三角剖分得计算公式为

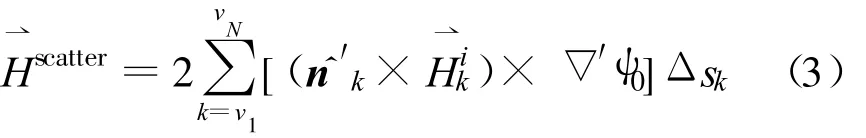
其中,k为能被观察点看到的三角面元的索引值,N为能被观察点看到的三角面元的总数,为第k个三角面元外法向单位矢量,为入射场第k个三角面元入射磁场,Δsk为第k个三角面元的面积。

3 可见三角面元识别法及存在问题

在传统的GRECO中,三角面元的识别方法如图1所示。

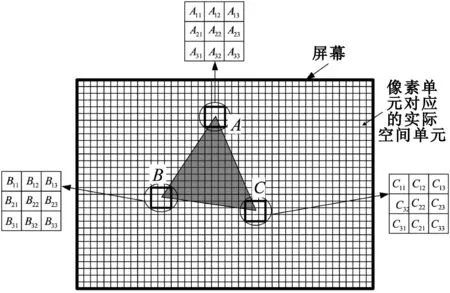
图1 可见三角面元识别方法Fig.1 The identification of the triangular facets

其具体步骤为:

(1)建立A点与屏幕坐标的关系从而确定A点对应屏幕上第A22个像素;

(2)确定与像素 A22相距最近的屏幕像素A11～A33;

(3)读取像素 A11～A33处的深度缓存区中对应位置的深度值,并根据深度坐标变换关系求出实际的z坐标值;

(4)比较 A点处的z坐标值与像素A11～A33处的实际的z坐标值,并设置标志lflag1,只要像素A11～A33处实际的z坐标值与A点处z坐标值的差的绝对值小于ε,则使 lflag1增加 1,如果 lflag1≥1,则认为A点可见;

(5)同样的步骤对B点和C点进行处理,如果B点和C点亦可见,则三角面元可见。

当三角面元尺寸远远大于像素对应的实际空间的尺寸时,这种方法是可行的,但是对于电大尺寸的目标,三角面元的尺寸将小于像素对应的实际空间尺寸,可见的三角面元将无法被识别出来。

4 多区域算法

本文引入了多区域算法,即把可视区域分区域分别在屏幕上显示,可使得像素对应的实际空间的尺寸缩小,可以达到三角面元尺寸远远小于像素对应的真实空间的尺寸。图2显示了同一个目标在不同区域划分下的成像。

图2 划分为2×2个区域目标成像图Fig.2 The target imaging with 2×2 divisions

基于多区域方法,计算了图3立方体目标的远场RCS,立方体尺寸为0.3 m×0.3 m×0.3 m,入射频率9.375 GHz,模型图、文献[14]结果如图3所示,划分成不同区域时的计算结果如图4所示。

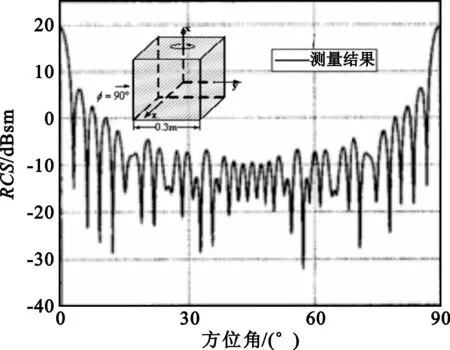
图3 模型及文献[14]测量结果图Fig.3 The cube model and its measurement result in Reference[14]

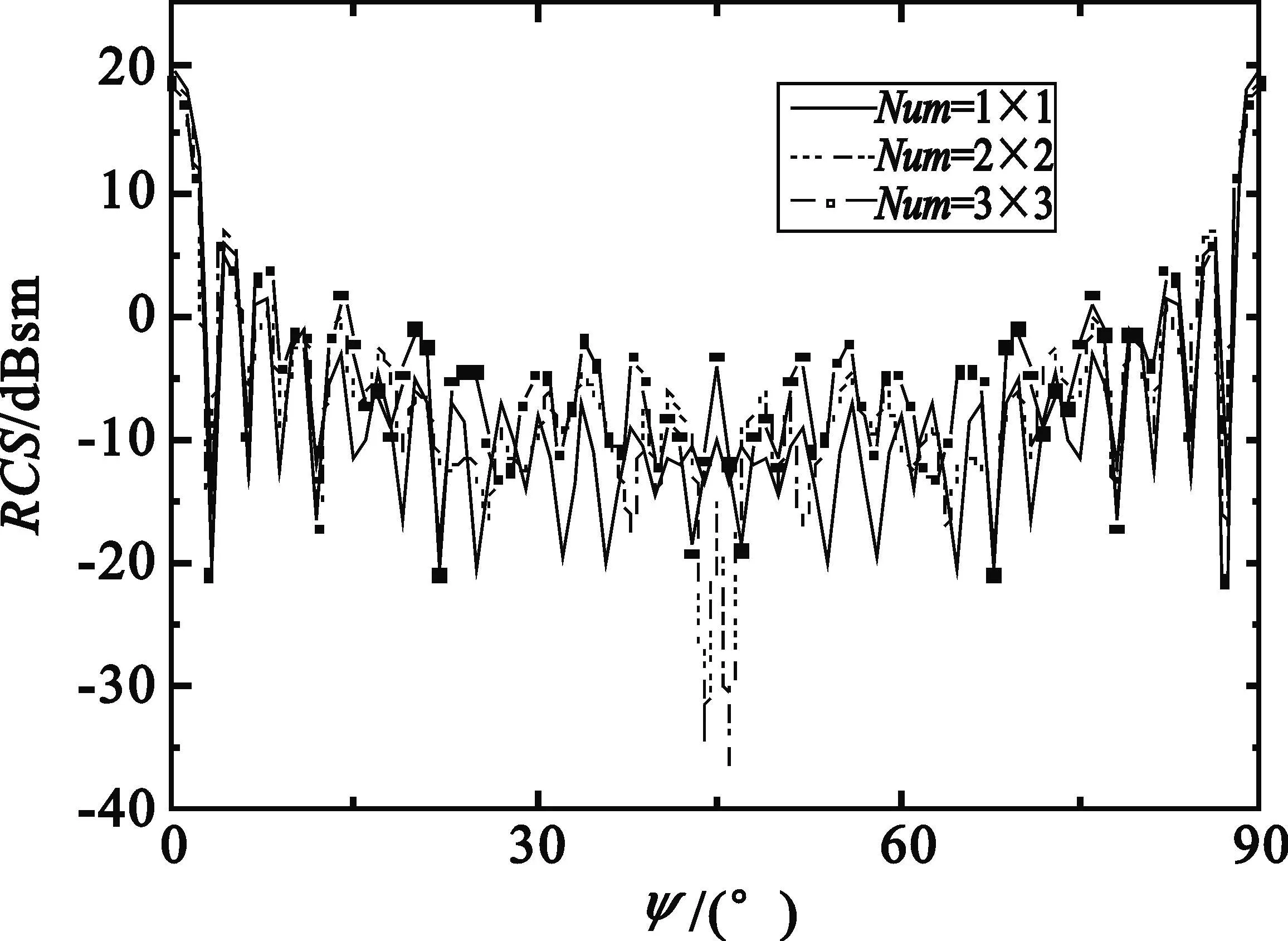
图4 不同区域划分多区域算法计算结果Fig.4 The computed result of multi-region method with different divisions

从计算结果可以看出,当可视区域未被剖分时,由于此目标尺寸较小,计算结果与文献[14]结果吻合得很好,但是当可视区域被剖分多个区域时,则计算结果反而存在较大的误差。其具体原因为:当采用多区域方法时,相邻区域存在着识别盲区,如图5所示,阴影部分三角面元不能被识别,从而导致计算结果偏差。

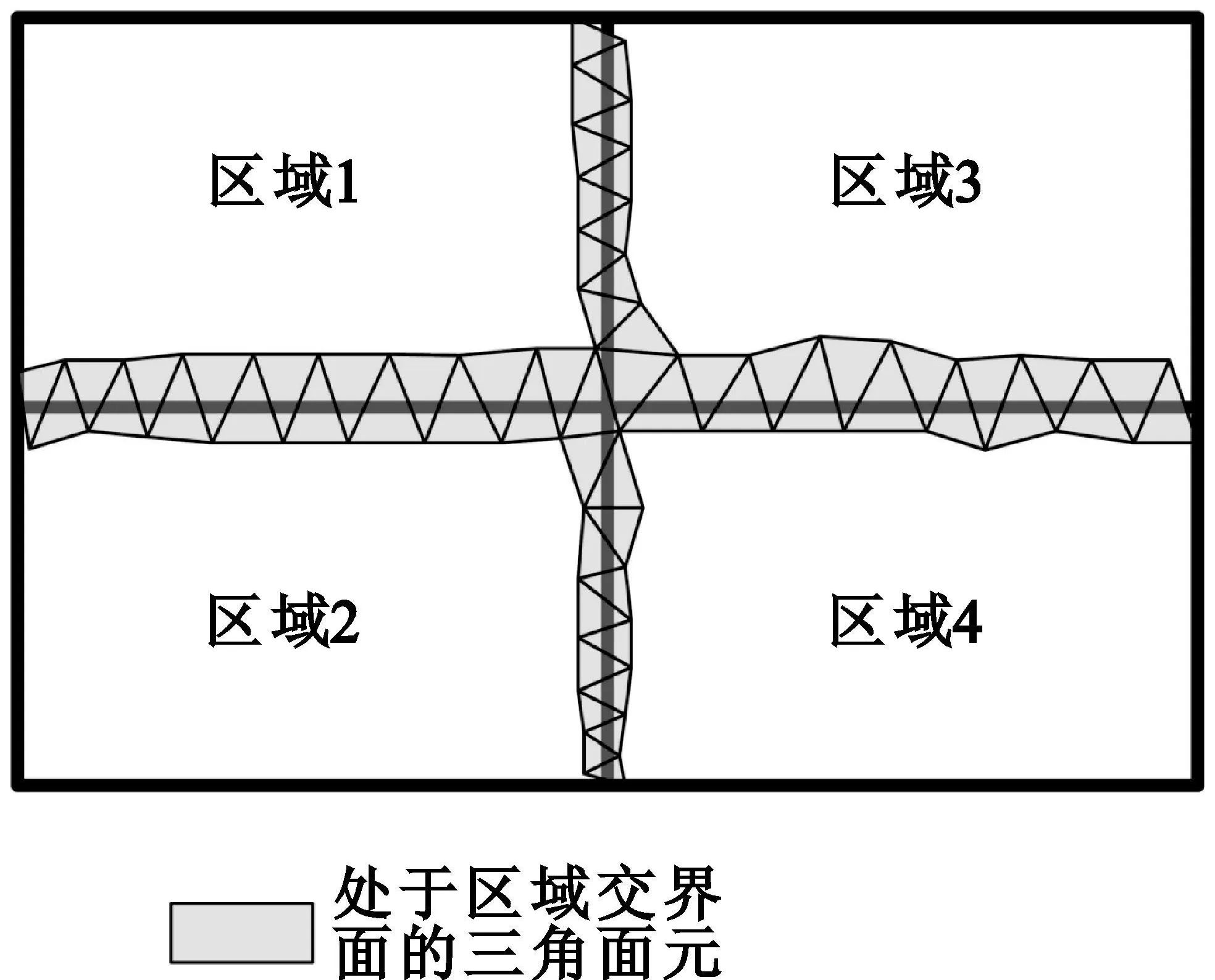
图5 多区域算法存在的识别盲区Fig.5 The blind zone of the multi-region method

5 虚拟屏幕法

为了解决多区域算法导致的识别盲区问题,本文提出了一种新方法——虚拟屏幕法,下面详细介绍这种新方法的步骤。

(1)根据目标的尺寸确定可视区域的范围,即确定可视区域左下部顶点(xleft,ybottom)和可视区域右上部顶点(xright,ytop)的坐标值;

(2)根据目标的尺寸及屏幕的分辨率确定需要分成的区域数Nnum=Nx×Ny,Nx为在x轴向分成的区域的个数,Ny为在y轴方向分成的区域的个数;划分依据是每个像素大小不大于λ/20;

(3)建立一个虚拟的屏幕,此屏幕包含Nnum个子屏幕,建立每一个子屏幕上的屏幕像素坐标与虚拟屏幕像素坐标的关系;

(4)确定虚拟屏幕上每一个像素点处的信息;

(5)基于虚拟屏幕,识别出能被光源照到的三角面元。

虚拟屏幕算法的关键是确定子屏幕上的像素坐标与虚拟屏幕上的像素坐标之间的对应关系,这样就可以很容易地识别出可见三角面元。基于多区域GRECO的虚拟屏幕相当于将屏幕分辨率提高了Nnum倍。需要注意的是,在边界可见面元识别过程中,要按一定规则判断边界可见面元归属问题,以避免重复计算。

6 计算结果

基于虚拟屏幕法重新计算了图3所示正方体在不同区域划分时的雷达散射截面,计算结果如图6所示。

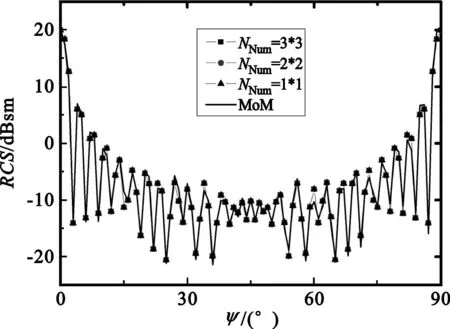
图6 多区域GRECO虚拟屏幕法不同区域划分结算结果比较Fig.6 The computed result of the virtual screen algorithm with different divisions

由计算结果可知,在3种不同区域划分的情况下,正方体RCS的计算结果吻合良好,并且基于多区域虚拟屏幕法计算出的结果与文献[14]中的结果是一致的。

图7为某型飞机的简易模型,为准确计算其RCS,本文方法将可视区域被划分为Nnum=20×15,入射频率9.375 GHz。采用虚拟屏幕法计算,并与成熟的商业软件FEKO的仿真结果进行比较,结果如图8所示。

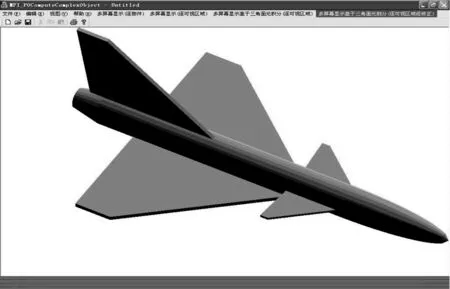
图7 某型飞机模型Fig.7 A plane model

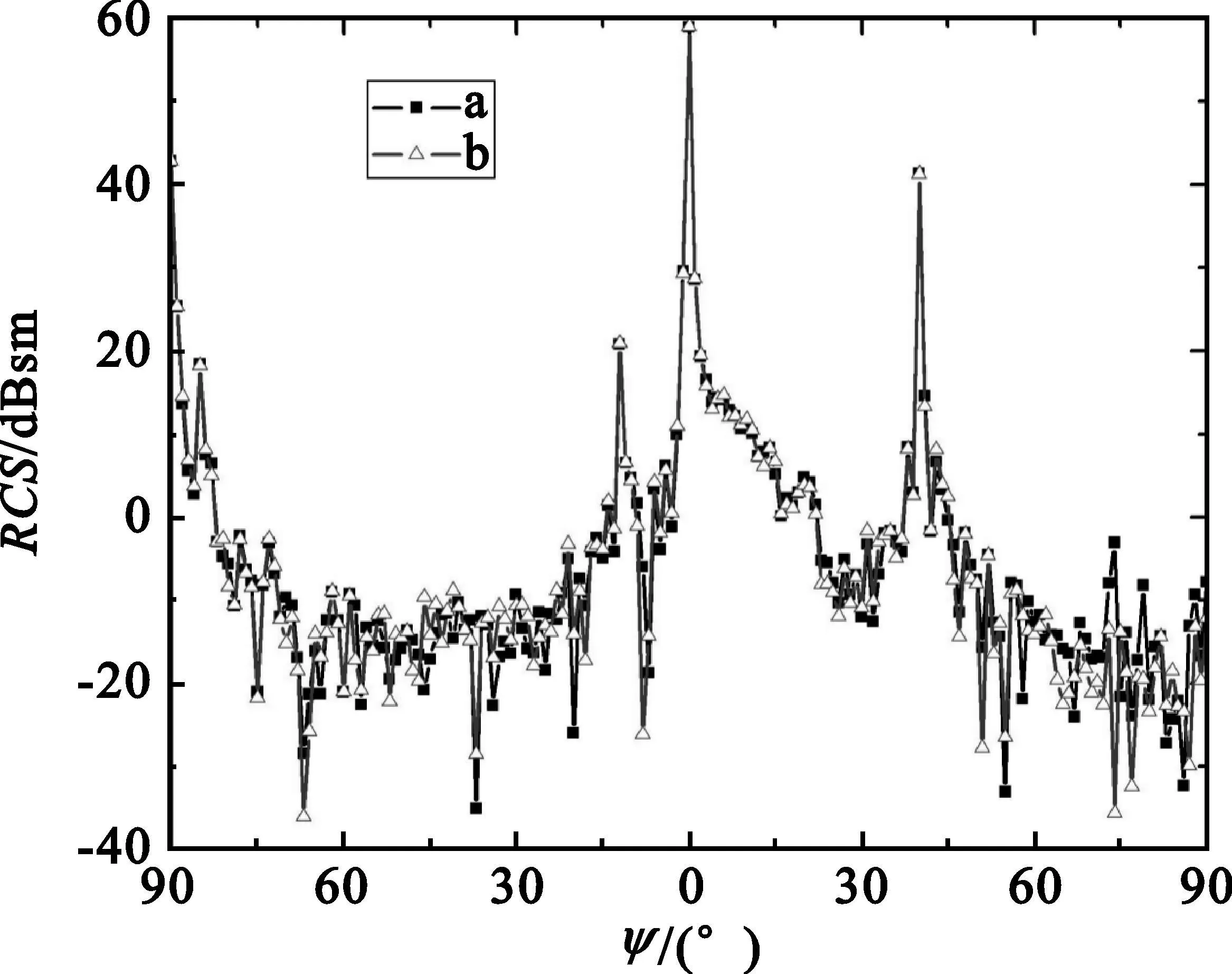
图8 某型飞机模型RCS计算结果Fig.8 The RCS of the plane model

图8中,曲线a表示基于三角面元剖分的多区域GRECO虚拟屏幕算法的计算结果,曲线b为商业软件FEKO的仿真结果。从上述计算结果可以看出,利用两种方法计算的结果吻合得很好。计算结果存在微小的偏差是由于两种方法采取的对可见面的积分方法不一样,虚拟屏幕算法是基于物理光学法,而FEKO是基于快速多级子技术。

7 结 论

通过采用多区域GRECO虚拟屏幕法,不仅解决了传统GRECO方法屏幕分辨率小与目标电尺寸大的矛盾,同时解决了多区域方法存在边界盲区的问题,使得对于观察点可见的目标的三角面元都可准确地识别出来,进而可基于PO法准确计算目标RCS。通过数值算例,验证了多区域GRECO虚拟屏幕法的正确性和有效性。计算结果完全满足工程需要,而且节省计算资源,计算速度快。多区域GRECO虚拟屏幕法还拓展了传统GRECO方法的应用范围,为利用IPO法分析存在多次散射的复杂电大尺寸目标的散射特性奠定了基础。

[1] Tsukerman I.Electromagnetic Applications of A New Finite-Difference Calculus[J].IEEE Transactions on Magnetics,2005,41(7):2206-2225.

[2] Liu Peng,JinYa-Qiu.An FEM Approach With FFT Accelerated Iterative Robin Boundary Condition for Electromagnetic Scattering of a Target With Strong or Weak Coupled Underlying Randomly Rough Surface[J].IEEE Transactions on Antennas and Propagation,2005,53(12):4137-4144.

[3] Yla-Oijala P,Taskinem M.Calculation of CFIE Impedance Matrix Elements with RWG an n×RWG Functions[J].IEEE Transactions on Antennas and Propagation,2003,51(8):1837-1846.

[4] Rius JM,Parrón J,Heldring A,et al.Fast Iterative Solution of Integral Equations With Method of Moments and Matrix Decomposition Algorithm-Singular Value Decomposition[J].IEEE Transactions on Antennas and Propagation,2008,56(8):2314-2324.

[5] Geng N,Sullivan A,Carin L.Multilevel Fast-Multipole Algorithm for Scattering from Conducting Targets Above or Embedded in a Lossy Half Space[J].IEEE Transactions on Geoscience and Remote Sensing,2000,38(4):1561-1573.

[6] Waltz C,Sertel K,Carr M A,et al.Massively Parallel Fast Multipole Method Solutions of Large Electromagnetic Scattering Problems[J].IEEE Transactions on Antennas and Propagation,2007,55(6):1810-1816.

[7] Pinel N,Johnson J T,Bourlier C.A Geometrical Optics Model of Three Dimensional Scattering From a Rough Surface Over a Planar Surface[J].IEEE Transactions on Antennas and Propagation,2009,57(2):546-554.

[8] Sanyal S,Bhattacharyya A K.Electromagnetic Scattering by a Curved Plate-Solution by Uniform Asymptotic Theory of Diffraction[J].IEEE Transactions on Antennas and Propagation,1984,32(2):187-189.

[9] Pelosi G,Tiberio R,Puccini S,et al,Applying GTD to Caculate the RCS of Polygonal Plate[J].IEEE Transactions on Antennas and Propagation,1990,38(8):1294-1297.

[10] Hestilow J.Simple Formulas for the Calculation of the Average Physical Optics RCS of a Cylinder and a Flat Plate Over a Symmetric Window Around Broadside[J].Antennas and Propagation Magazine,2000,42(5):48-52.

[11] Weinmann F,Ray Tracing With PO/PTD for RCS Modeling of Large Complex Objects[J].IEEE Transactions on Antennas and Propagation,2006,54(6):1797-1806.

[12] Zhao Kezhong,Vouvakis M N,Lee Jin-Fa.The Adaptive Cross Approximation Algorithm for Accelerated Method of Moments Computations of EMC Problems[J].IEEE Transactions on Antennas and Propagation,2005,47(4):763-773.

[13] 张云飞,马骏.复杂目标GRECO方法的分屏显示计算[J].北京航空航天大学学报,2005,31(112):1332-1336.ZHANG Yun-fei,MA Jun.Multi-screen display calculation method of GRECO for complex targets[J].Journal of Beijing University of Aeronautics and Astronautics,2005,31(112):1332-1336.(in Chinese)

[14] 李建周.复杂目标一体化电磁散射计算与优化研究[D].西安:西北工业大学,2005.LI Jian-zhou.The integrated electromagnetic scattering computing and optimization research of complex target[D].Xi′an:North-West Industrial University,2005.(in Chinese)