改进的宽带信号有理数倍采样率变换结构

邹 维,达新宇,谢铁城,王 舒

(空军工程大学电讯工程学院,西安 710077)

1 引 言

数字接收机的设计与实现中需要对模拟信号数字化,为了不造成频谱的混叠和运算能力的浪费,不同信号要求不同的采样率;另外,为了使同一信号得到最优的处理,在接收机系统的不同模块所要求的采样率也不同[1-3]。因此,对经过ADC采样后的离散数字信息进行采样率变换,使整个系统尽可能地接近最佳值,是接收机系统设计与实现过程中重要技术之一。

对于窄带系统,有理数倍采样率变换已有较为成熟的研究[4-7],对于宽带接收系统,不仅要求系统有较高的采样率,而且A/D输出的高数据流要求硬件平台有极高的处理能力,因此,存在电路实现的瓶颈。为了避免高频率工作电路的产生,文献[8]在传统采样率变换结构的基础上,通过对内插器与多相滤波器组的等效变换,得出了一种避免高时钟数字电路的等效结构,但这种方案电路实现复杂,滤波电路靠前且电路的工作频率为ADC的采样率,改进程度不大;文献[9]提出了一种交换抽取器和内插器的等效的采样率变换结构,但这种结构需要ADC的采样为过采样且处理后的信号会产生镜像信息,需要另外的镜像滤波器来处理信号。

为此,本文从有理数倍采样率变换的基本原理出发,分析和研究了抽取器、内插器的结构和顺序,运用等效结构的变换原理,给出了有理数倍采样率变换的等效结构,并对改进的结构进行了仿真验证。结果表明,改进后的有理数倍采样率变换结构性能良好,运算效率是传统方案的LM倍(L和M分别是内插和抽取倍数),适用于宽带信号的采样率变换。

2 有理数倍采样率变换的基本原理

假设x(n)为待处理的原序列,y(n)为采样率变换后的序列;对其进行L倍内插相当于在原序列x(n)的两点之间等间隔的插入L-1个零点,内插后的序列的频谱Y(ω)=X(Lω),那么内插后的频谱进行了L倍的压缩。

抽取是内插的逆过程,对原序列进行M倍的抽取相当于在原序列x(n)的基础上每隔M-1个点取一个点得到新的抽取序列y(n),其频谱Y(ω)=抽取完后的频谱将是将原序列的频谱进行M倍扩展同时幅度变为原频谱的1/M,由各个频谱叠加而成的抽样频谱。

有理数倍采样率变换是由内插器和抽取器级联实现的,先内插后抽取,内插后的序列频谱压缩 L倍,会形成镜像信息,为了消除不必要的高频成分需要对内插后的信号进行滤波;同样,对于抽取后的信号频谱会扩张会造成频谱的混叠,在抽取前需要进行抗混叠滤波,故整个有理数倍的抽取过程如图1所示。

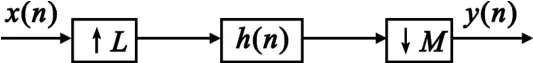
图1 有理数倍转换结构Fig.1 The transformational structure of rational number times

3 有理数倍采样率变换的等效变换

通常情况下对非整数倍的有理数倍采样率变换是先内插后抽取,变换后的采样率符合Nyquist定理就不会造成基带信号的丢失;同样,如果先抽取后内插,经过抽取后的采样率符合Nyquist定理也不会造成基带信号的丢失;因此,过采样是有理数倍采样率变换等效结构的前提。图2为等效变换后的有理数倍采样率变换结构图。

图2 等效后的有理数倍采样率转换Fig.2 Transformation of rational rates after equivalence

原始序列x(n),经过抽取器后为v(k),那么抽取后的频谱 V(ω)为

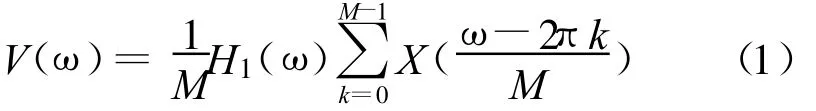
对v(k)进行内插后有

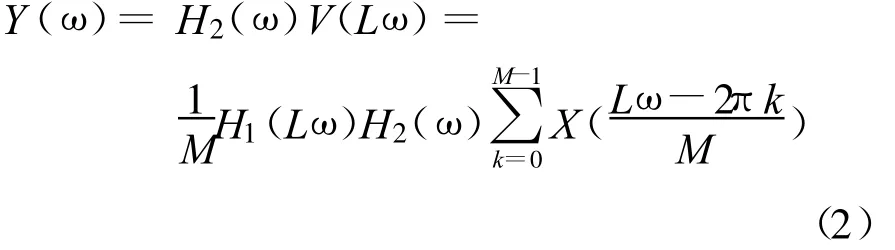
由式(1)和式(2)可知,两者的滤波器都为了变换后的信号不发生混叠或抑除镜像信号,如果低通滤波器理想的情况下,式(1)等效于

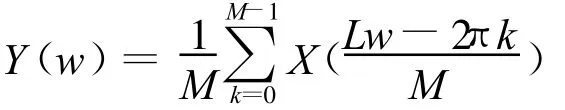
所以等效结构中

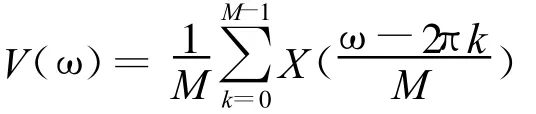
公式(2)可以写成

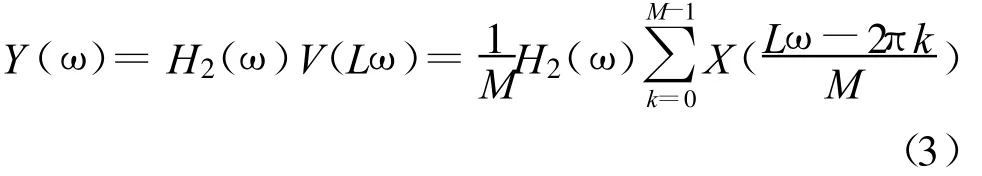
H2(ω)是防止变换后的信号产生镜像信息的滤波器,所以滤波器理想的情况下式(1)和式(2)是等效的,故有理数倍的采样率变换可以先抽取后内插。

4 改进的有理数倍采样率变换

常用的有理数倍采样率转换结构无法满足宽带信号的采样率变换。如果我们对采样率变换的结构进行等效变换,先抽取后内插,那么滤波电路的工作频率不是输入频率就是输出频率,这样就避免了高频率的工作电路。为了进一步的降低工作频率,根据等效变换,多相滤波可以进一步降低滤波电路的工作频率;经过抽取后的信号 y(m)=

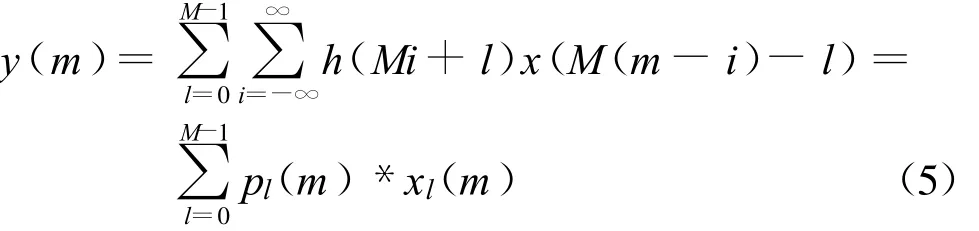
整个过程可以理解为先对x(n)进行M倍抽取然后与pl(i)卷积,l为某一状态的时延,所以抽取器的多相结构可表示为图3。

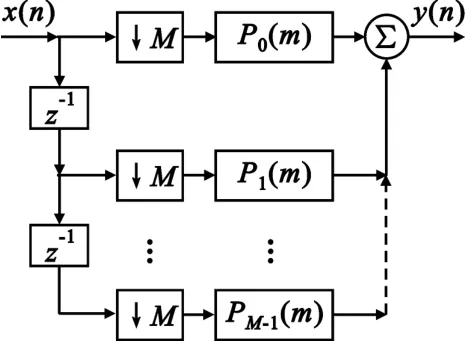
图3 多相抽取结构Fig.3 Multiphase extraction structure

同理,可得到内插器的多相结构图4。

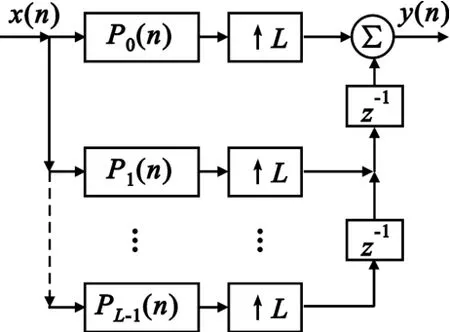
图4 多项内插结构Fig.4Multiphase interpolation structure

结合抽取器与内插器的多相结构和有理数倍采样率变换的等效图2可以得到一种改进的有理数倍采样率变换的结构图,如图5所示。

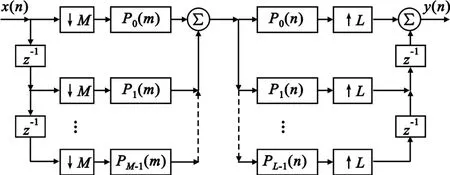
图5 改进后的有理数倍转换Fig.5 The improved transformation of rational rates

改进后的有理数倍采样率变换是先抽取后内插结构的多相结构,方案中所有的滤波电路工作在抽取后的工作频率下,假设原序列的采样率为fs,那么经过抽取后采样率变为 fs/M,采样率明显降低了;通常的有理数倍采样率变换先内插,内插后的采样率变为Lfs,采样率上升了,显然改进后的结构在滤波电路的工作频率只需要传统方案的1/LM倍,所以从运算效率来说改进后的方案优势明显。

5 结构仿真验证

为了验证上述改进结构的正确性,按照图5的改进方案做了仿真模拟。假设原始序列 x(n)=5;仿真中滤波器的设置采用Matlab提供的Firl(Q,wn)函数,Q为滤波器的阶数,wn为滤波器的截止频率;考虑到滤波器的延迟和设计需要Q=20。

按照改进方案和传统方案对序列进行有理数倍采样率变换,得到图6,可以看出(e)和(c)由于滤波器都存在一定的时延;从两者的频谱图可以看出改进的方案与传统的方案所到达的效果是一致的。

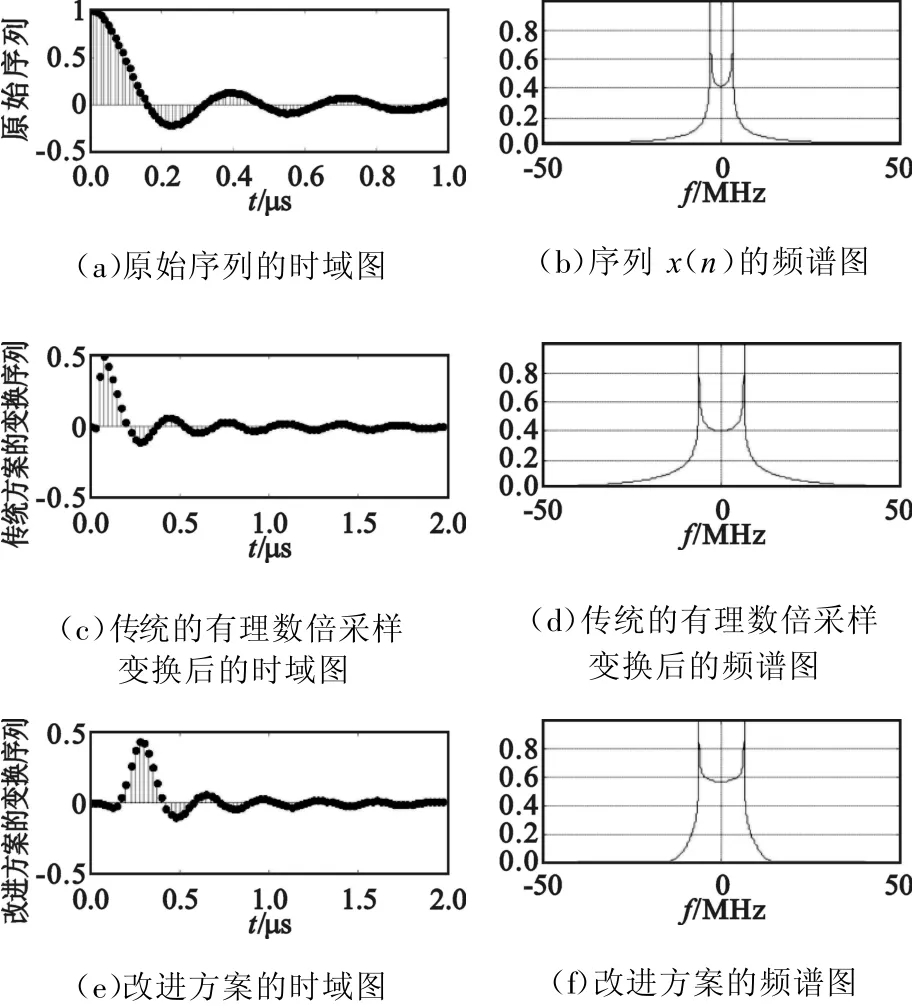
图6 改进方案与传统方案的仿真对比Fig.6 The simulation contrast between the improved scheme and the traditional one

在计算量上,传统方案滤波电路需要处理5 120×2个点,5路5 120×2/5个点卷积,每点卷积需要4次乘、3次加,5路5 120×2/5个加,共81 920次运算;改进的方案需要处理5 120/5个点,5路1 024/5个点卷积,每点卷积 4次乘、3次加,1 024个加,2路1 024/2个点卷积,每点卷积10次乘、9次加,1 024个加,共10 240次运算;改进后的结构运算量为传统结构的1/8倍,运算量明显降低。

可以看出改进后的方案序列上没有失真,频谱的变换大致是一致的,功率谱也是一致的,所以改进的方案在转换效果上是与传统方案等效的,但从运算效率上来说,改进的方案大大提高系统的运行效率,不需要电路工作在较高的工作频率下,有利于实际电路的实现。

6 结 语

本文在分析交换采样率变换顺序的基础上,得出了等效变换的前提条件,即信号的采样频率必须得是过采样,进而提出了一种针对高频率工作电路的有理数倍采样率变换结构,改进后的结构不仅节约了运算和存储资源,而且具有相对稳定的可靠性,在实际中具有重要的应用价值。然而,该结构的高效率是牺牲掉了信号的一部分信息,所以要想获得更加准确和高效的有理数倍采样率变换结构有待进一步的研究。

[1] 粟欣,许希斌.软件无线电原理与技术[M].北京:人民邮电出版社,2010:52-61.SU Xin,XU Xi-bin.The Principles and Techniques of Software radio[M].Beijing:Posts and Telecommunications Press,2010:52-61(in Chinese).

[2] 陶然,张惠云,王越.多抽样率数字信号处理理论及其应用[M].北京:清华大学出版社,2007:55-63.TAO Ran,ZHANG Hui-yun,WANG Yue.Sampling rate digital signal processing theory and application[M].Beijing:Tsinghua University Press,2007:55-63.(in Chinese)

[3] 王德海,步兮瑶.多采样率系统[M].北京:电子工业出版社,2008:57-70.WANG De-hai,BU Xi-yao.Multirate system[M].Beijing:Publishing House of Electronics Industry,2008:57-70.(in Chinese)

[4] Ascheid G,Oerder M,Stahl J,et al.An all digital receiver architecture for bandwidth efficient transmission at high data rates[J].IEEE Transactions on Communications,1989,37(8):804-813.

[5] Tseng C H,Chou S C.Direct down-conversion of multiband R F signals using bandpass sampling[J].IEEE Transactions on Wireless Communications,2006,5(1):72-76.

[6] Kamperman F L A J.Design of an all digital direct-sequence spread-spectrum receiver[C]//Proceedings of 1994 IEEE International Symposium on Personal,Indoor and Mobile Radio Communication.Hague:IEEE,1994:18-23.

[7] Ahmed N Y,Ashour M A,Nassar A M.Power efficient polyphase decomposition comb decimation filter in multirate telecommunication receivers[C]//Proceedings of 2008 Mosharaka International Conference on Communications,Propagation and Electronics.Amman:IEEE,2008:1-6.

[8] 肖振宇,苏厉,金德鹏,等.宽带全数字接收机的分数倍采样率变换[J].清华大学学报,2010,50(10):1641-1645.XIAO Zhen-yu,SU Li,JIN De-peng,et al.Fractional sampling rate transformation for wideband all digital receivers[J].Journal of Tsinghua University(Science&Technology),2010,50(10):1641-1645.(in Chinese)

[9] 刘春霞,王飞雪.分数倍采样率转换中内插与抽取的顺序研究[J].电子技术应用,2005,6(5):44-45.LIU Chun-xia,WANG Fei-xue.The research about the order of decimation and interpolation in Fractional sampling rate transformation[J].Application of Electronic Technique,2005,6(5):44-45.(in Chinese)