USB信号相位解调器的改进设计
梁 昊,赵 琦,刘 曦
(北京航空航天大学电子信息工程学院,北京 100191)
1 引 言
微波统一测控系统是一种利用公共射频信道,将航天器的跟踪测轨、遥测、遥控和天地通信等功能合成一体的无线电测控系统。微波统一S频段(U-nified S Band,USB)系统将各种信息先分别调制在不同频率的副载波上,然后相加共同调制到一个S频段载波上发出;在接收端先利用载波环对载波进行捕获,在载波锁定之后利用相位解调器进行相位解调,最后用不同频率的滤波器将各副载波分开,解调各副载波信号,得到发送时的原始信息[1]。
一般USB系统调相信号的解调思路是首先对采样后的调相信号进行正交下变频,然后对正交分解出的同相分量 Acos[φ(n)]以及正交分量Asin[φ(n)]进行反正切运算[2-3]。
在对某型号USB应答机的研制过程中,发现这种方法在解调过程中会出现两个不足之处:首先是随着数据精度的要求不断提高,在反正切查表的过程中对ROM容量的要求不断增大,目前一般采取的办法是不断增加硬件资源,然而这带来的后果是系统越来越庞大,冗余资源越来越多;其次,在反正切的过程中,当作为分母的同相分量Acos[φ(n)]等于0时,系统将进行除0运算,目前一般的解决办法是对这些点进行是否为0的判断,如果同相分量为0,则根据正交分量的符号直接判断解调相位为±90°。
本文通过利用 CORDIC算法,完成了基于CORIDC算法的反正切模块,利用此模块设计了一种相位解调器,较好地弥补了查表法解调的不足之处,并且在基带滤波处理阶段设计了一种通用型的带通滤波器,用于分离各个副载波。
2 CORDIC算法实现反正切函数
2.1 CORDIC算法实现反正切函数的原理
CORDIC算法基本原理如图1所示。
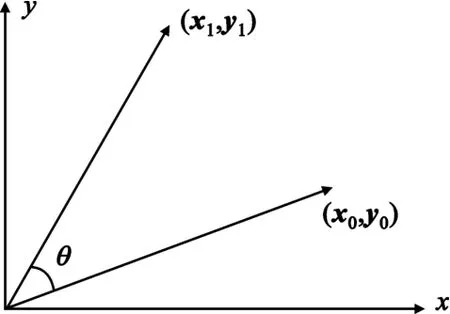
图1 CORDIC算法基本原理Fig.1 The principle of CORDIC
初始向量(x0,y0)旋转 θ角度之后得到向量(x1,y1),此向量有如下关系[4]:
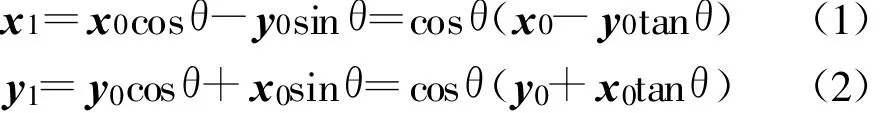
假设初始向量(x0,y0)经过N次旋转转向(x1,y1),且第 i次旋转角度为δ=arctan(2-i),则第 i步旋转可以表示为
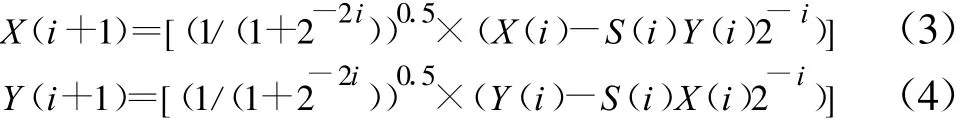
其中,(1/(1+2-2i))0.5称为校模因子,当旋转次数大于一定值时,趋于常数0.607 3。S(i)=1或-1,表示旋转角度的方向,逆时针为1,顺时针为-1。
基于CORDIC实现反正切函数,就是把坐标平面内一点的坐标(x0,y0)旋转到X轴,并且记录所旋转的角度值,该值就是所要得到的反正切函数值。
假设有一初始向量(x0,y0),在旋转的过程中首先进行对纵坐标值 y的符号进行判断,当y大于0时顺时针旋转,当y小于0时,逆时针旋转,容易得到角度 θ≈ ∑S(i)δ(i),迭代一定次数后 θ就是所要求得的反正切函数值。
从上可以看出,通过迭代的方法,只需要加减法器和移位器就可以实现反正切函数的运算。
CORDIC算法一般可通过迭代法和流水线法实现[5]。迭代法运算的实时性较差,但需要的硬件资源较少;流水线法需要比迭代法多迭代次数倍的资源,具有较好的实时性特点。由于USB接收机对数据处理的实时性要求较高,因此本文的反正切模块采用流水线结构。
2.2 迭代次数对CORDIC算法实现反正切函数的影响
在数据运算长度不变的情况下,影响CORDIC算法运算精度的主要因素是CORDIC的迭代次数。对于反正切模块,主要体现在旋转角度的次数上,迭代次数过低,有可能会使向量(x0,y0)旋转不到距离X轴很近的位置,而旋转结束后(x0,y0)与X轴的夹角就是由于迭代次数不够产生的误差。因此,估计迭代次数对CORDIC算法实现反正切函数的影响可以通过迭加剩余未旋转的角度完成,即
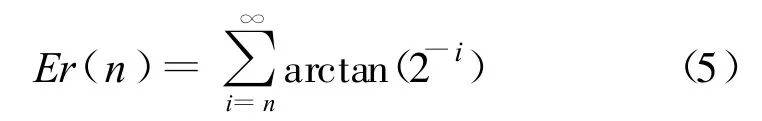
其中,n为迭代的次数。
仿真计算结果如图2所示。
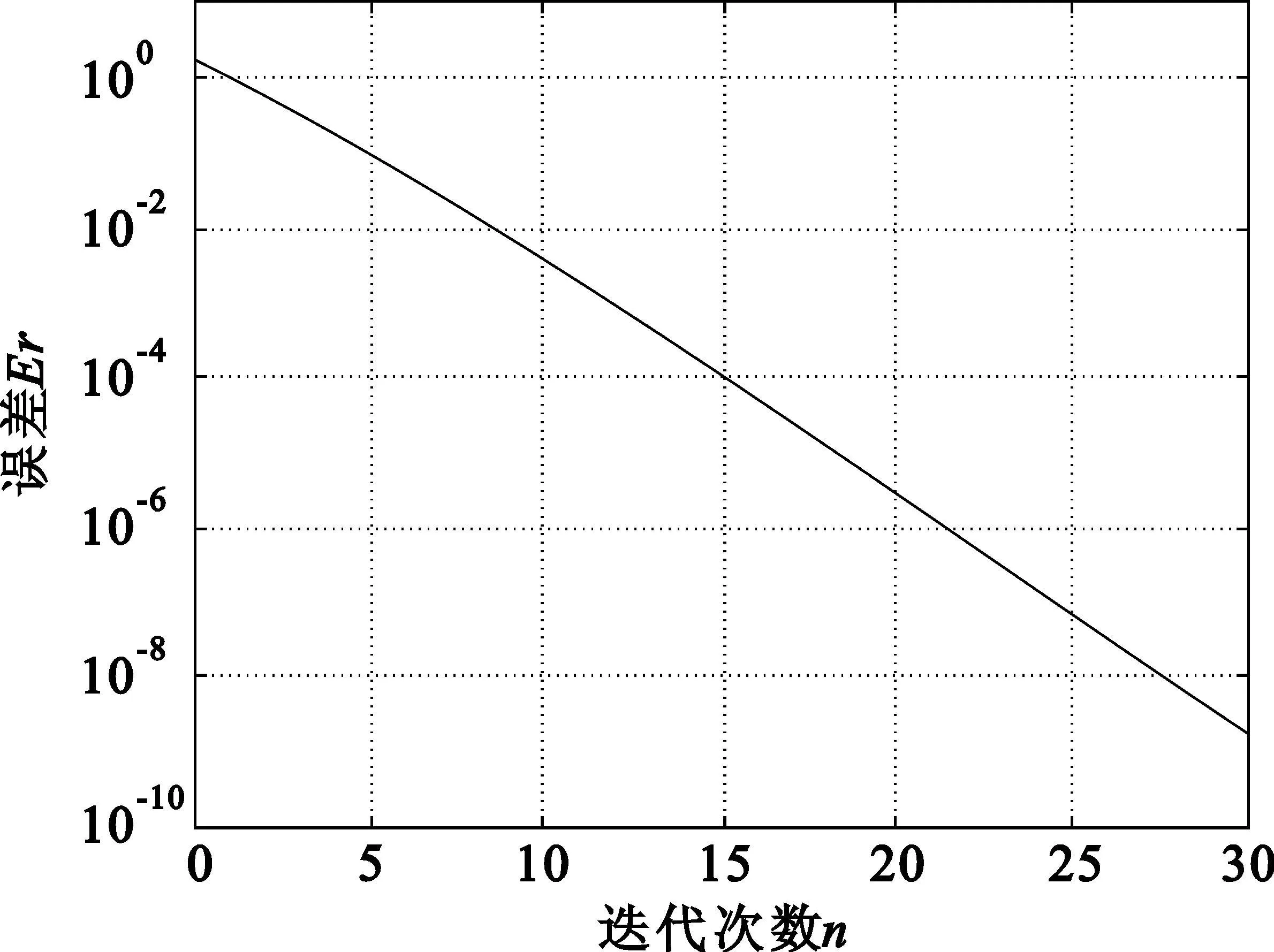
图2 迭代次数对CORDIC算法实现反正切函数的影响Fig.2 The number of iterations′affection on the arctangent function based on CORDIC
经过曲线拟合之后可得到经验公式:
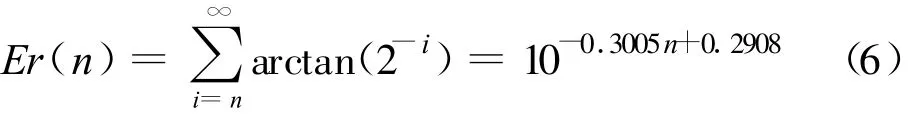
3 基于CORIDC算法的USB相位解调器的设计
3.1 反正切法解调USB中频调相信号
对于一个多副载波的USB中频调相(Phase modulation,PM)信号,包含的信息包括遥测信息(调制方式为PCM-BPSK-PM)、遥控信息(调制方式为PCMQPSK-PM)、测距音信息(调制方式为直接PM),其数学表达式为
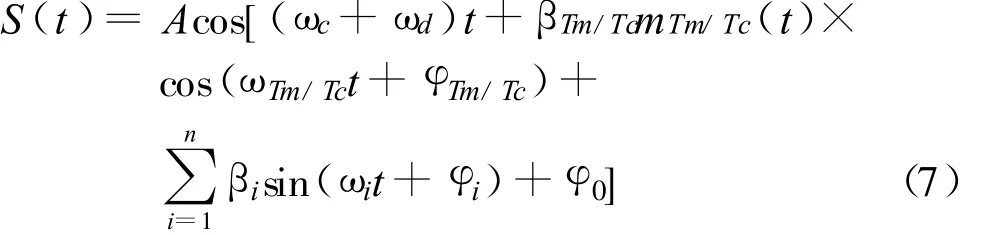
式中,ωc、ωd、ωTm/Tc、ωi分别为载波频率 、多普勒频率、遥测或遥控副载波频率、测距音频率;βTm/Tc、βi分别为遥测或遥控副载波调制度、测距音调制度;φTm/Tc、φi、φ0分别为遥测或遥控副载波初相位 、测距音初相位、载波初相位;mTm/Tc(t)为遥测码或遥控码[6]。令
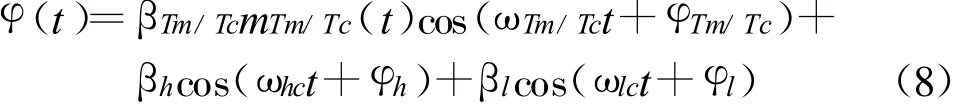
对信号采样后进行正交下变频,得同相分量和正交分量如下:
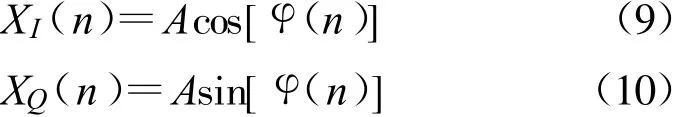
把同相分量输入到CORDIC反正切模块的X接口,正交分量输入到Y,就可求出
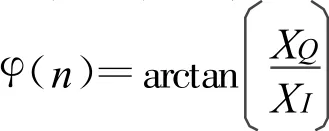
即解调出了相位信息。具体实现方法如图3所示。
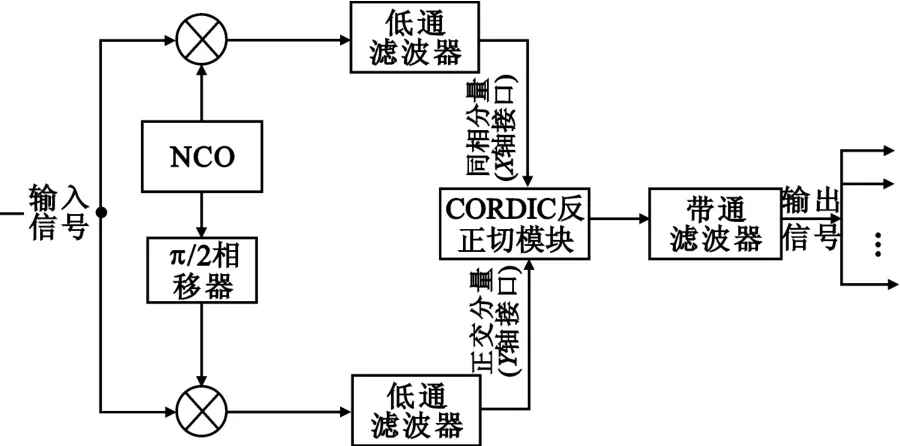
图3 基于CORDIC的USB相位解调器Fig.3 USB phase demodulation based on CORDIC
在SIMULINK平台下,仿真结果图4所示。
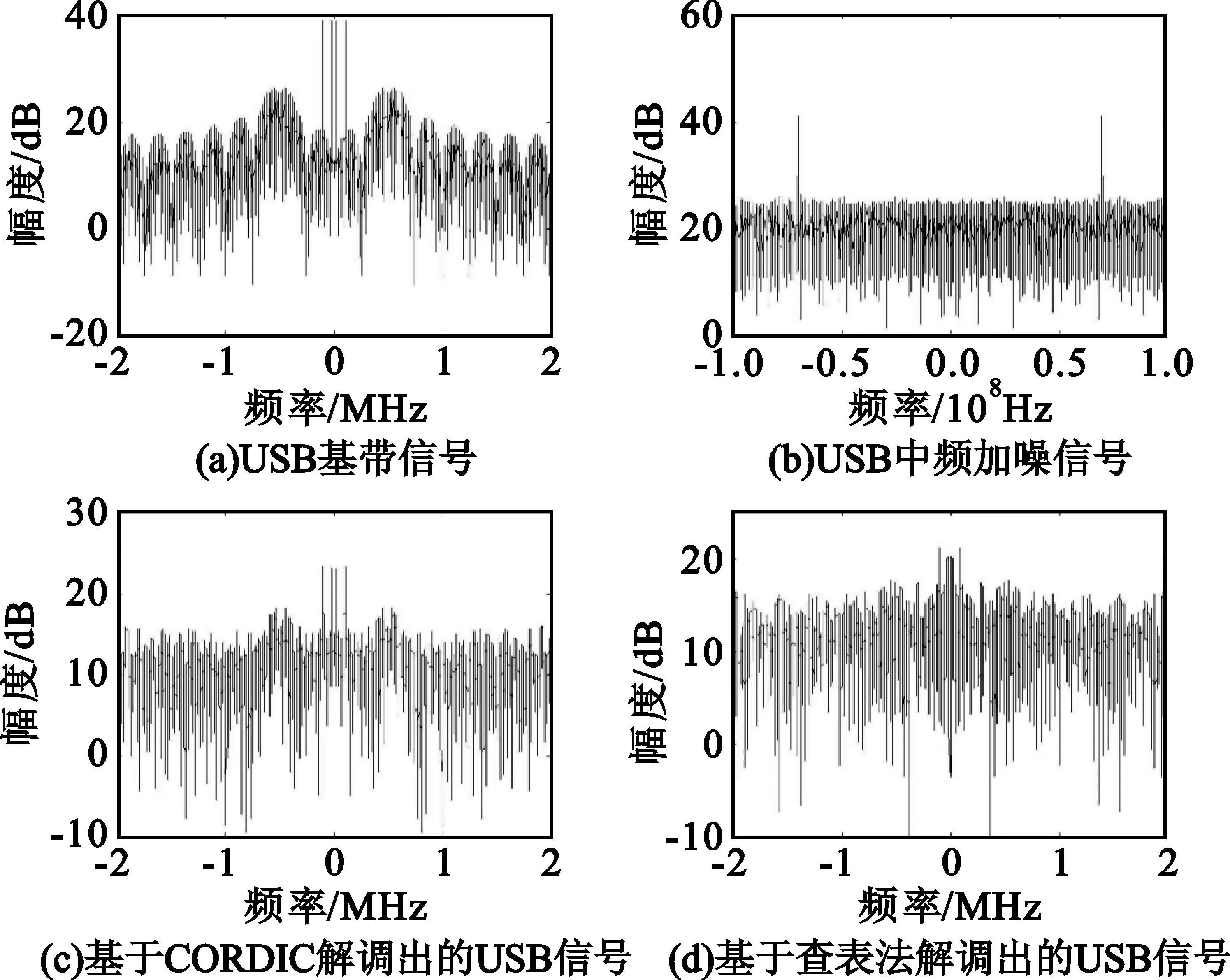
图4 USB相位解调器仿真结果Fig.4 The simulation result of USB phase demodulation
由图4可以看出,基于CORDIC算法反正切模块的解调方法和基于查表法在解调性能上基本一致,但是使用基于CORDIC算法的相位解调器有两个查表法所不具备的优点。首先,作为一种迭代算法,CORDIC能够大大节省硬件资源,例如查表法相位码取17位,幅度码取12位,则所需的ROM值为12×217≈1.5M,而CORDIC算法所占的硬件资源还不到1K,要增加反正切的计算精度只需增加迭代流水线中模块的个数而不用按指数比例增加ROM的容量。其次,基于CORDIC算法的解调模块由于采用坐标旋转的方法,在迭代运算的过程中只存在加减和移位运算,不会出现查表法中除0的问题。
另外,在仿真过程中,发现CORDIC算法在计算过程中根据迭代次数的不同会产生不同的群延迟。然而,因为CORDIC算法在每一次旋转运算过程中所消耗的运算资源几乎一样,因此不会产生不确定的延迟误差,对下行转发的测距信号不会产生影响。
3.2 USB信号的基带滤波器的设计
所谓USB信号基带滤波,就是把USB下变频信号的各个频谱分量分离,得到独自的遥测或遥控信号、主侧音和次侧音。
本文设计了如图5所示的带通滤波器进行基带滤波。首先把USB基带信号中所要得到分量的频谱搬移到原点位置,再通过低通滤波器滤除不需要的其他高频分量,最后把原点处的频谱上变频到原来的位置。
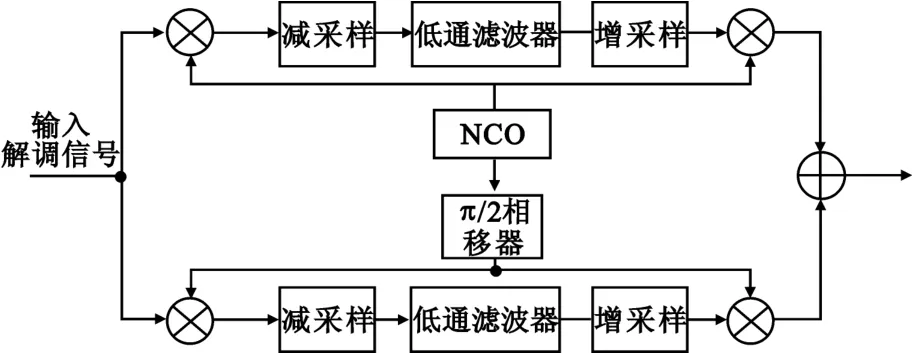
图5 带通滤波器设计Fig.5 The design of band-pass filter
设输入解调信号为
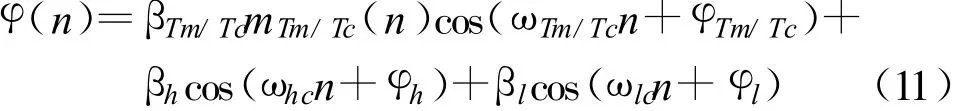
假设需要得到遥测或遥控信号,首先在NCO中输入预设的载频 ωTm/Tc得到 I/Q两路输入分别为cos(ωTm/Tcn)、sin(ωTm/Tcn),再分别与 φ(n)相乘,之后经过减采样,测距音信号被抑制,经过低通滤波器和增采样之后,第I路和第Q路分别为
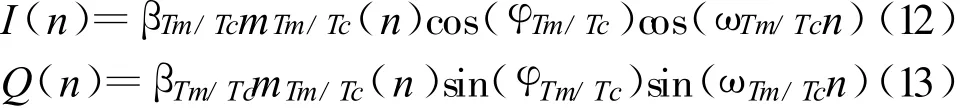
经过加法器,可得
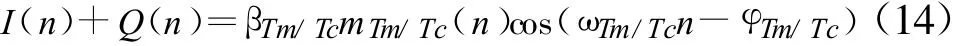
即分离出了独立的遥测/遥控副载波。
这种滤波器的优点在于:3种滤波通道可使用相同的结构,只需要改变NCO本振频率即可;而且混合相位信号中只存在PSK副载波和测距单频两种类型的信号,因此只需要设计两种不同通带宽度的低通滤波器。
通过基带带通滤波器可以分别滤出主、次侧音信号以及遥控遥测信号,仿真结果如图6所示。
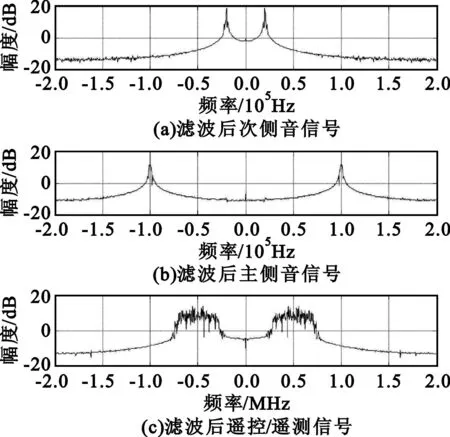
图6 基带滤波后的结果Fig.6 The result of baseband filter
4 结 论
本文设计了基于CORDIC算法的反正切模块,估算出迭代次数对反正切模块运算精度的影响,利用反正切模块设计了一种基于CORDIC算法的USB信号相位解调器,除此之外在基带处理阶段设计了一种通用型带通滤波器。仿真结果表明:基于CORDIC算法的USB相位解调器,能够较好地解决解调USB调相信号时查表法产生的ROM容量限制问题和系统除0问题,基带处理阶段设计的通用型带通滤波器可以有效分离副载波信号和主、次侧音信号。因此,基于CORDIC算法的相位解调器以及通用型带通滤波器都可以作为今后研制USB调相信号解调模块的一种有效参考。
另外,在研究基于CORDIC算法的USB相位解调器的时候遇到了这样一个问题,即使通过判断输入向量的象限将CORDIC反正切函数的值域从-π/2~π/2扩展到-π~π,但当各个副载波的调制度之和大于π时,即公式(6)中则解调不出对应的调相信号。在本文的基础上,这个问题值得继续研究。
[1] 王培慈.USB测控信号特性分析及其中频模拟器的设计与实现[D].长沙:国防科学技术大学,2008.WANG Pei-ci.The Characteristic Analysisof USBTT&C Signal and the Corresponding IF Simulator′s Implementation[D].Changsha:National University of Defense Technology,2008.(in Chinese)
[2] 姜宇柏,游思晴.软件无线电原理与工程应用[M].北京:机械工业出版社,2007:207-239.JIANG Yu-bo,YOU Si-qing.Software radio principles and engineering applications[M].Beijing:China Machine Press,2007:207-239.(in Chinese)
[3] 占荣辉.星用双模应答机综合基带PM模式关键技术研究[D].长沙:国防科学技术大学,2003.ZHAN Rong-hui.A Research on Some Key Techniques in the Integrated Base-band of PM Modeabouta Dual-mode Transponder[D].Changsha:National University of Defense Technology,2003.(in Chinese)
[4] Vo1der J E.The CORDIC Trigonomitric Computing Technique[J].IEEE Transactions on Electronic Computers,1959(8):330-334.
[5] 耿丹.CORDIC算法研究与实现[J].遥测遥控,2007,(增1):39-42.GENG Dan.Research and implementation of CORDIC algorithm[J].Journal of Telemetry;Tracking and Command,2007(S1):39-42.(in Chinese)
[6] 侯孝民,陈源,张书仙.统一测控系统下行信号仿真器设计与实现[J].国外电子测量技术,2010(1):69-76.HOU Xiao-min,CHEN Yuan,ZHANG Shu-xian.Design and implementation of down-signal simulation in unified TT&C system[J].Foreign Electronic Measurement Technology,2010(1):69-76.(in Chinese)

