面向有向赋权网络的节点重要性度量方法研究

单海燕

（南京信息工程大学经济管理学院，南京 210044）

面向有向赋权网络的节点重要性度量方法研究

单海燕

（南京信息工程大学经济管理学院，南京 210044）

众多现实问题可以建模为有向赋权网络中节点重要性的度量问题。文章从节点不同连接方式的角度出发，区分网络中节点的直接连接、桥梁连接以及间接连接方式对有向赋权网络的损失，提出了面向有向赋权网络的节点相对重要性的度量方法；通过对比节点重要性不同度量方法，说明该方法能更细致地凸显节点之间的差异性，并比较客观地反映节点的物理属性以及节点的网络结构位置对有向赋权网络整体的影响作用。

有向赋权网络；相对重要性；直接损失；间接桥梁损失；间接连接损失

0 引言

通讯网络、交通网络、供应链网络、知识网络等许多现实系统中存在多种复杂关系，如合作关系、运输关系、生产关系、社会关系等[1～3]。网络中哪些个体对网络的连通性及各种关系的建立会起到至关重要的作用？通讯网络中如何选择最有效的节点作为传播源点对整个网络进行信息传播？城市交通网络中哪些路口发生拥堵会造成交通系统瘫痪？知识网络中哪些个体的流失将给组织带来重大损失？这些问题都可归结为个体/节点在系统/网络中的重要性问题，均是现实中亟待解决的问题。

本文将针对有向赋权网络，赋予节点一定的物理属性及势，从节点不同连接方式的角度出发，区分网络中节点的直接连接、桥梁连接以及间接连接方式对有向赋权网络的不同损失，提出有向赋权网络中节点重要性的测度方法，并通过实例说明该方法能更有效地评估网络中节点的重要性。

1 节点重要性的度量模型

1.1 基本定义

有向赋权网络可以通过图G=(N,E,W)表示，其中N={1,2,…,n}表示网络中所有节点的集合，E={e1,e2,…,em}表示网络中所有边的集合，W={wi1i2,wi1i3,…,win-1in}表示网络中所有边上权重（关系强度）的集合。

可采用社会网络中的邻接矩阵表示有向赋权网络结构，邻接矩阵中的行和列表示网络中的各节点，并且行和列排列的顺序都相同，矩阵中行位置的行动者通常是某种特定关系的发送者，列位置的行动者通常是某种特定关系的接收者；矩阵中的元素，代表行动者之间是否存在某种关系，这样的矩阵X记作

1.2 节点重要性的度量方法

1.2.1 直接损失

在有向赋权网络中删除某节点后，将给网络中可直接获得该节点相关资源或信息的这些节点产生最直接影响。假设节点j可直接获得节点i的相关资源或信息，即xji=1。如果相对节点j，节点i在某类度量指标上的势较大且节点j与节点i建立的关系强度较强，那么删除节点i后节点j的损失较多，反之亦然。因为，若相对节点j，节点i在某类度量指标上的势较大，说明节点i有更多的资源或信息值得节点j去学习或获取；关系强度越强，说明节点j越容易获得或接收到节点i的相关资源或信息。因此，删除节点i后有向赋权网络的直接损失可定义为定义1删除节点i后有向赋权网络的直接损失NLD(i)可表示为

1.2.2 间接桥梁损失

在有向赋权网络中删除节点i后，也可能给网络中未直接与节点i建立连接的一些节点产生影响。例如，在有向赋权网络中，若节点j经过节点i获得节点k的相关资源或信息，那么，删除节点i后，将给节点j获得节点k的相关资源或信息产生不便，可能需经过更长的路径，甚至无法到达节点k。这里将这类间接损失定义为间接桥梁损失。

假设d(i,j,k)表示在可经过节点i的情况下，节点j到节点k的最短路径长度，不妨将这条最短路径表示为j→h1→…→hdi→k，令Hi(j,k)={h1,…,hdi}；d(-i,j,k)表示在不经过节点i的情况下，节点j到节点k的最短路径长度，不妨将这条最短路径表示为j→h-1→…→hd-i→k ， 令 H-i(j,k)={h-1,…,hd-i}， 显 然iH-i(j,k)。

注意一下几点：

(1)由于机会成本以及时间成本的存在，一般认为有向赋权网络中的节点选择最短路径来获取网络中其他节点的资源或信息。

（3）如果i∉Hi(j,k)，说明节点j可不经过节点i获得节点k的相关资源或信息，那么Hi(j,k)=H-i(j,k)，并且d(i,j,k)=d(-i,j,k)。

（4）如果Hi(j,k)=，即节点j无法到达节点k，显然H-i(j,k)=∅且d(i,j,k)=d(-i,j,k)=+∞，说明任意节点在建立节点j与节点k连接方面并未起到桥梁作用。因此，可近似将删除节点i对节点j与节点k的损失看作0。

（5）如果Hi(j,k)≠∅但H-i(j,k)=∅，说明在删除节点i前，节点j经过节点i可到达节点k，但删除节点i后，节点j无法到达节点k，即节点i在建立节点j与节点k连接方面起到桥梁作用。若节点k的势不低于节点j的势，那么删除节点i将给网络中的节点造成不小的损失。

（6）如果Hi(j,k)≠∅且H-i(j,k)≠∅，说明删除节点i，可能使得网络中剩余节点需经过更长的路径才能与其他节点建立连接。

定义2删除节点i后，对有向赋权网络中节点j(j∈N{i,k})与节点k(k∈Γi)间的间接桥梁损失NLIB(i,j,k)可表示为：

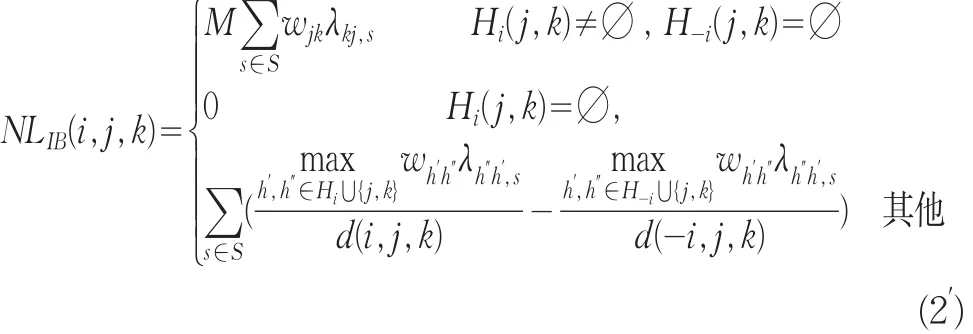
其中，M为一很大的正数。

因此，删除节点i后有向赋权网络的间接桥梁损失NLIB(i)可表示为：

1.2.3 间接连接损失

另一方面，删除节点i也会给网络中通过间接连接方式获得节点i的资源或信息的那些节点产生损失。对邻接矩阵X进行乘法运算，可分析出有向赋权网络中间接获得节点i的资源或信息的节点数并找出相应的间接连接路径。

1.2.4 节点重要性的测度

这里我们将节点重要性的测度等价为该节点被删除后对网络中剩余节点的破坏性（损失）。因此，节点的重要性可定义为：

定义4有向赋权网络中节点i的重要性NI(i)表示为

其中,α、β、γ≥0分别表示在度量节点重要性时，删除节点i将给网络造成的直接损失、间接桥梁损失以及间接连接损失的权重，且α+β+γ=1。

定义5有向赋权网络中节点i的相对重要性RNI(i)可定义为：

2 模型分析

为了更好地理解几种典型的节点重要性判断方法的差异性，探讨本文所提出的度量方法的有效性和适用性，这里以文献[4]给出的数据为例，对几种典型的节点重要性判断方法的计算结果进行比较分析。

图1 有向赋权网络图

表1 节点直接损失、间接桥梁损失以及间接连接损失计算结果

从表1可以看出，相同节点在有向赋权网络的不同网络结构下，具有不同的直接损失、间接桥梁损失以及间接连接损失，从而具有不同的网络地位。有向赋权网络中的节点若具有相对较优的网络结构位置及较高的势，那么这类节点的流失将给网络造成较大的损失，如图1（i）、（iii）中的节点1与节点5。反之，若节点的网络结构位置较劣或节点的势相对较低，节点在有向赋权网络中地位较低，如图1（ii）中的节点1，虽然节点1的势相对较高，但网络中其他节点并未关注到该节点。

表2对本文及文献[3]、[4]所给的节点重要性判断方法的排序结果进行比较。由于文献[6]、[12]均针对无向网络进行研究，因此表2给出的文献[6]、[12]排序结果可看作是针对图1（i）的分析结果。对比这三种度量方法，我们发现这种对图1（i）中节点1在网络中的重要程度的分析结果是一致的，但在其他节点重要性的分析上出现了分歧。文献[3]所给方法分析出节点6是网络中最不重要的节点，然而本文认为是节点2与节点3，文献[4]认为是节点2。由于节点2具有最低的势且未起到任何“桥梁”作用，因此删除图1（i）中的节点2，对网络中其他节点不会造成损失；若删除节点3，虽然节点3不是网络中势最低的节点，势比它低的节点（节点2与节点5）是通过间接连接的方式获得节点3的相关信息或知识，但是节点2与节点5可以通过直接连接方式获得比节点3还要多的信息或知识，因此删除节点3也不会对网络中其他节点造成损失；但是删除节点6会导致节点5可能无法直接获得更多的信息或知识，节点6不会是网络中地位最低的节点。

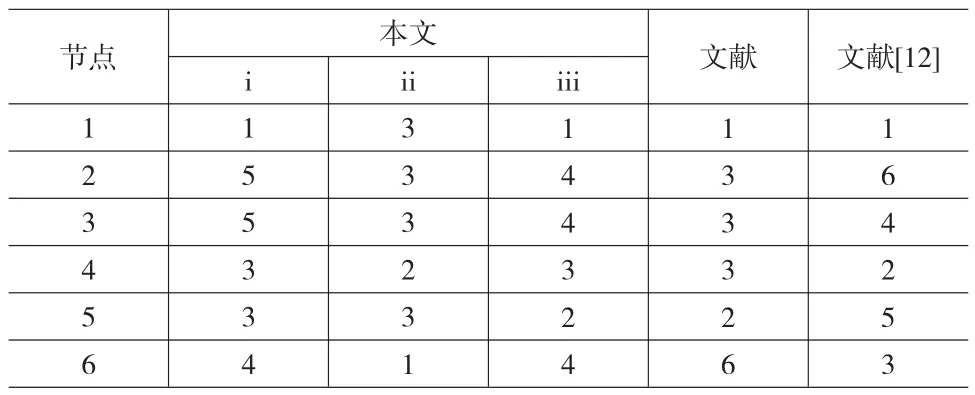
表2 节点重要性度量方法对比

通过对比不同的节点重要性度量方法，表明本文提出的有向赋权网络节点重要性的度量方法能更细致地凸显节点之间的差异性，并比较客观地反映节点的物理属性以及节点的网络结构位置对网络整体的影响。因此，本文所提出的方法具有广泛的实用性以及对现实网络具有指导价值。

[1]Song X,Wang X,Li A,et al.Node Importance Evaluation Method for Highway Network of Urban Agglomeration[J].Journal of Transportat⁃lon Systems Engineering and Informatlon Technology,2011,11(2).

[2]Cowan R,Jonard N.Network Structure and the Diffusion of Knowledge[J].Journal of Economic Dynamics and Control,2004,28(8).

[3]Okumura Y.A network Formation Process Converges to the Complete Collaboration Network[J].Mathematical Social Sciences,2007,53(2).

[4]王建伟,荣莉莉,郭天柱.一种参数可调的网络节点重要性度量方法[J].科研管理,2009,30(4).

[5]安世虎,聂培尧,贺国光.节点赋权网络中节点重要性的综合测度法[J].管理科学学报,2006,9(6).

[6]单海燕,王文平.面向产量决策的多寡头网络最优结构分析[J].管理科学学报,2010,13(5).

F27

A

1002-6487（2012）24-0029-03

国家自然科学基金资助项目（70973017；71172044）

单海燕（1981-），女，江苏盐城人，博士，讲师，研究方向：系统建模及网络分析。

（责任编辑/易永生）