拟蒙特卡洛方法中Halton序列的随机化及其改进

木拉提·吐尔德，胡锡健

(新疆大学 数学与系统科学学院，乌鲁木齐 830046)

拟蒙特卡洛方法中Halton序列的随机化及其改进

木拉提·吐尔德，胡锡健

(新疆大学 数学与系统科学学院，乌鲁木齐 830046)

Halton序列是简单并且容易实现的低差异序列。Wang和Hickrnell[1]提出的随机化Halton序列在高维的情形下会产生高度相关情况，并且在高维情形下估计精度和收敛速度都很差。文章结合随机化和置乱化方法改善了Halton序列这些缺点。模拟结果表明，改进的随机化Halton序列在精度和相关性方面都好于随机化Halton序列。

—Halton序列；低差异序列；置乱化；随机化；数字积分

0 引言

自1960年Halton提出Halton序列以来，低差异序列在拟蒙特卡洛（QMC）方法中的应用非常广泛。Halton序列是简单的非常容易实现的低差异序列，但是最大的缺点是在高维的情况下会产生高度相关的情况，使得模拟的精度和收敛速度都非常差，为了改进Halton序列这个缺点，人们提出了一系列的改进方法。1979年Braaten和weller[2]根据一维偏差率最小的原则提出了的置乱化（scrambling）Halton序列，1995年Owen[3]提出了线性置乱化Halton序列，2000年Wang和Hickrnell[1]提出的随机化Halton序列，2004年Atanassovet[4]提出了可以使模拟的误差边界最小的Halton序列等。

本文拟结合随机化方法和置乱化方法使对Wang和Hickrnell提出的随机化Halton序列在高度相关和收敛速度方面进行改进，并且通过实际模拟来说明改进的随机化Halton序列在高维的情况下估计精度和收敛速度都比文献[1]的随机化Halton序列要好。

1 随机化Halton序列

首先简单地介绍经典van der corput序列，一维的Halton序列实际上就是Van der corput序列。其次来介绍文献[1]提出的随机化Halton序列。

1.1 经典的Van der corput序列

如果b≥2的整数，对于任意的n≥0可以写成以基为b的展开式

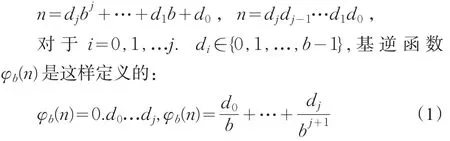
Halton序列是Van der corput序列的扩展，一维的Halton序列是实际上就是Van der corput序列，多维的Halton序列则是由不同的素数为基的Van der corput序列构成。可表示为：

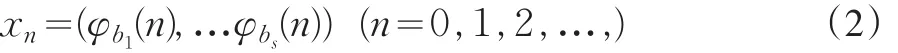
1.2 随机化Halton序列

随机化Halton序列[1]要从φb(n)得到φb(n+1)，我们只需要给φb(n)加1 b得到φb(n+1)，这个加法不是普通的加减法这叫做向右进位加法⊕（rightward carry addition）。

Van Neumann-Kakutani变换定义：若b≥2的整数，对于x∈[0,1)，我们把x写成如下形式：

定义向右进位加法（rightward carry addition）⊕，为：

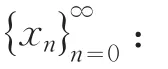
2 置乱化（scrambling）Halton序列

因为Halton序列随维数的增加会产生高度相关的点列。为了消除这个高度相关现象，人们提出了置乱化（scrambling）方法。第一次正式的提出这个方法的是Braaten和weller[5]

像（1）式中基逆函数φb(n)一样定义了置乱化的（scrambled）基逆函数Sb(n)：

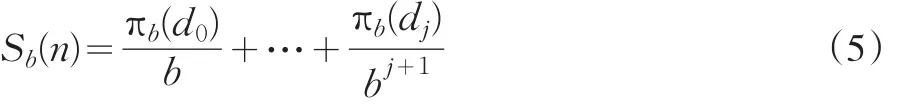
这里πb是在数集(0,1,…,b-1)中的置换，则确定的置乱化Halton序列记作：

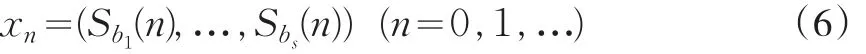
3 改进的随机化Halton序列

改进的目的是使随机化Halton序列在高维的情形下相关性得到改善并且在使得随机化Halton序列分布更均匀更随机。改进方法如下：

第一步：假设在一维的情况下，基为b。对于任意x0∈[0,1]s，则按照公式（4）得到T(x0)。

第二步：对得到T(x0)进行置乱化变换，由公式（3）可知uk是取自于集合(0,1,…,b-1)的数。我们提出的置换如果uk≠0则把uk用b-uk来代替。即：

则对于任意xn∈[0,1]s一维改进的随机化halton序列是

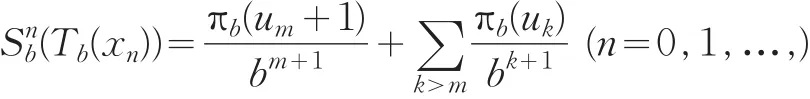
如果对于任意xn∈[0,1]s基为b1,b2,…bs的s维多维改进随机化halton序列是

由定理1可知序列{T(xn)}∞0也是在[0,1]s上均匀分布的随机向量。并且很容易证明序列Sn(T(xn))的误差收敛率也是O(N-2(logN)2s)。

如图1(b)所示，随机化Halton序列在高维的情况下会产生相关性，这样均匀性被破坏了并且估计方差也会很大。改进随机化避免了这种相关性，见图1（a）。

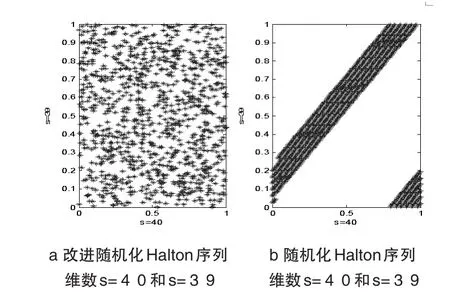
图1

4 模拟研究

下面考虑在s维[0,1]s下函数 f(x)的多重积分

表1 随机化Halton序列和改进随机化Halton序列模拟结果

表1是随机化Halton序列和改进随机化Halton序列在维数s=10,s=20,s=30,s=40,s=50时,并且所取的点数N=5000，N=10000，N=20000时多重积分 I(f)估计值和估计的样本方差。

随机化halton序列记作：rhalton，改进随机化halton序列记作irhalton。

5 结论

从表1可以看出，在维数从10维到50维变化时改进随机化Halton序列的估计样本标准差比随机化Halton序列要小，并且40维以后随机化Halton序列估计值明显比改进随机化Halton序列要差。这时两种方法都要求计算的函数值个数N要足够大，才能达到满意的精度。在估计的同时发现随着计算函数值的个数N的增大随机化Halton序列计算估计值的时间也非常长，而改进随机化Halton序列则比随机化要短很多。

[1]Wang,X.，Hickernell,F.J.Randomized Halton Sequences[J].Math.Comput.Modeling,2000（,32）.

[2]Braaten,E.,Weller,G.An Improved Llow-Discrepancy Sequence for Multidimensional Quasi-Monte Carlo Integrationp[J].Journal of Com⁃putational Physics,1979（,33）.

[3]Owen,A.B.Randomly Permuted(t,m,s)-nets and(t,s)-sequences.In Monte Carlo and Quasi-Monte Carlo Methods in Scientific Comput⁃ing,H.Niederreiter and P.J.-S.Shiue,Eds.Number 106 in Lecture Notes in Statistics[M].New York：Springer-Verlag,1995.

[4]Atanassov,E.，Durchova,M.Generating and Testing the Modified Halton Sequences[C].In Fifth International Conference on Numerical Methods and Applications,Borovets Springer-Verlag,Ed.Lecture Notes in Computer Science,2002.

[5]Wang,X.,Sloan,I.H.Why are High-dimensional Finance Problems of low Effective Dimension?[J].SIAM Journal on Scientific Computing,2005（,27）.

O211

A

1002-6487（2012）24-0015-03

新疆大学科学基金资助项目（07020428008）

木拉提·吐尔德（1985-），男，新疆人，硕士，讲师，研究方向：概率统计。

（责任编辑/亦 民）