曲线积分第二中值定理“中间点”渐近性分析

林冬翠

(广西幼儿师范高等专科学校，广西南宁530022)

曲线积分第二中值定理“中间点”渐近性分析

林冬翠

(广西幼儿师范高等专科学校，广西南宁530022)

通过研究第一型曲线积分第二中值定理“中间点”的渐近性，将结论推广到积分第二中值定理“中间点”的渐近性。首先给出第一型曲线积分第二中值定理及其证明，得出一个结论，由这个结论推导出定积分第二中值定理相应的结果。所得结论推广了文献［1－3］中关于积分第二中值定理的结论。

第一型曲线积分;中值定理;中间点;渐近性

0 引言

关于定积分中值定理“中间点”渐近性研究的文献和结果有很多，并且取得了不少的成果。文献［4］研究了在连续区间上一元函数的积分中值定理。文献［5］研究了积分第一中值定理中间点当区间长度趋向于零时的渐近性，得出的结论对在某点不可微的函数仍然有效。文献［1］研究了当函数f(x)在区间上连续且存在(n－1)阶导数，函数g(x)在区间上存在m阶导数时，积分第二中值定理“中间点”的渐近性，并且得到一系列相关的推论。文献［2］研究了函数g(x)在区间［α，β］上连续且不变号，g(α)≠0，f(x)在区间［α，β］上单调连续，在α点处可微且f'(α)≠0时，积分第二中值定理中间点的渐近性。还研究了函数g(x)在区间［α，β］上连续且不变号，g(α)≠0，f(x)在区间［α，β］上单调连续，且存在n阶导数时，积分第二中值定理“中间点”的渐近性。文献［5］研究了函数g(x)在区间［α，β］上连续且不变号，g(α)≠0，f(x)在区间［α，β］上单调连续，且满足=A≠0，λ＞0和A是两个常数时，积分第二中值定理“中间点”的渐近性。文献［6］则是在文献［1－3］的基础上，归纳分析关于积分第一中值定理“中间点”的渐近性的一些结果，再进而推出与之对应的关于积分第二中值定理的结果。文献［6］中的结论分别是文献［1－3］的结论的推广。

然而，对于曲线积分中值定理“中间点”渐近性的研究比较少。文献［7］利用极限理论对第一型曲线积分中值定理“中间点”的渐近性进行了探讨，主要研究函数f(x，y)在光滑曲线上连续，在某点处存在一阶导数且不为零时曲线积分第一中值定理“中间点”的渐近性，所得到的结论是积分第一中值定理“中间点”的渐近性的相应推广。文献［8－9］研究了函数f(x，y)在光滑曲线上连续，在某点处存在n阶连续导数且在某点前(n－1)阶导数为零，n阶导数不为零时，曲线积分第一中值定理“中间点”的渐近性，所得的结论是积分第一中值定理“中间点”的渐近性的相应推广。文献［10］研究了函数f(x，y)在光滑曲线上连续，且满足给定条件下的曲线积分第一中值定理“中间点”的渐近性，得到的结论是文献［7－9］的结论的推广，其结论也是积分第一中值定理“中间点”的渐近性相应的推广。本文在文献［7－10］的基础上，讨论第一型曲线积分第二中值定理“中间点”的渐近性，推广了积分第二中值定理“中间点”的渐近性，得到的结论是文献［1－3］的结论的推广，其结论也是积分第二中值定理“中间点”的渐近性相应的推广。

1 预备知识

本节主要介绍本文用到的主要引理。

引理1［4］(积分第一中值定理)若f在［a，b］上连续，则至少存在一点ζ∈［a，b］，使得

引理2［4］(推广的积分第一中值定理)若f(x)与g(x)都在［a，b］上连续，且g(x)在［a，b］上不变号，则至少存在一点ζ∈［a，b］，使得

引理3［4］(推广的积分第二中值定理)设函数f在［a，b］上可积，若g为单调函数，则存在ζ∈［a，b］，使得

引理4［4］如果函数f(x，y)在光滑曲线C(A，B)上连续，则存在一点M(x0，y0)∈C(A，B)，使得，其中s表示曲线C(A，B)的长。

引理5［5］若函数f(x，y)在光滑曲线C(A，B)上连续，则存在一点M(x0，y0)∈C(A，B)(端点A，B除外)，使得，其中s表示曲线C(A，B)的长。

引理6［4］如果曲线C(A，B):x=x(t)，y=y(t)(α≤t≤β)是光滑的，函数f(x，y)在曲线C(A，B)上连续，那么第一型曲线积分存在，且

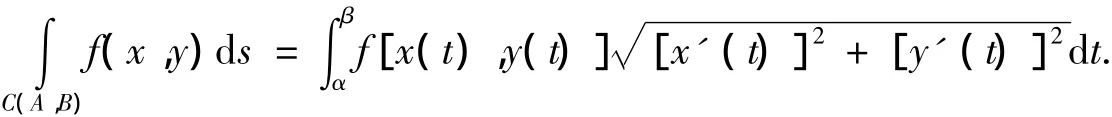
2 曲线积分第二中值定理中间点的渐近性

首先我们给出第一型曲线积分第二中值定理的证明。

定理1设函数g(x，y)在光滑曲线C(A，B):x=x(t)，y=y(t)(α≤t≤β)上可积.若f(x，y)是曲线C(A，B)上的单调函数，则存在一点M［x(ζ)，y(ζ)］∈C(A，B)(端点A，B除外)，使得

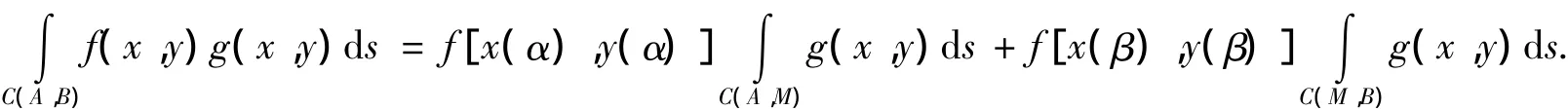
证明:由引理6得

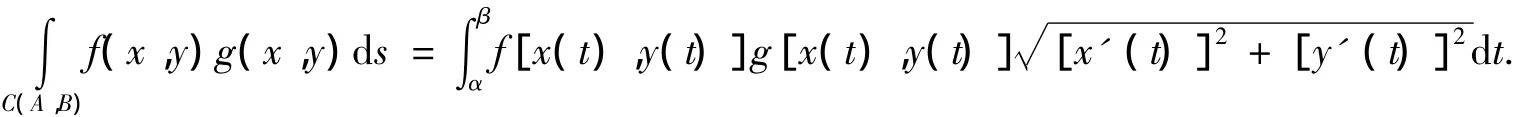
由引理3得

再由引理6得

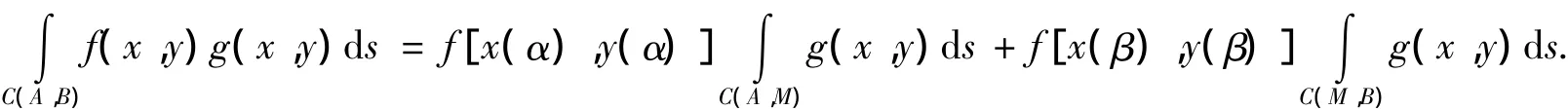
定理1获证。

关于曲线积分第二中值定理“中间点”的渐近性，我们可得到以下几个结论。

定理2如果曲线C(A，B):x=x(t)，y=y(t)(α≤t≤β)是光滑的，函数g(x，y)在曲线C(A，B)上连续，f(x，y)是曲线C(A，B)上关于参数t单调的函数，并且有实数q＞0，，实数p＞－1，这里h(t)=f［x(t)，y(t)］，k(t)=g［x(t)，y(t)］，A，B是两个常数，那么定理1中的中间点M［x(ζ)，y(ζ)］∈C(A，B)有渐近性，其中s*，s分别是曲线C(A，M)和C(A，B)的长。

证明:设“中间点”M［x(ζ)，y(ζ)］对应参数t=ζ，即x0=x(ζ)，y0=y(ζ)，则有α＜ζ＜β.由引理6得到

构造辅助函数

利用L’Hospital法则，我们可得到

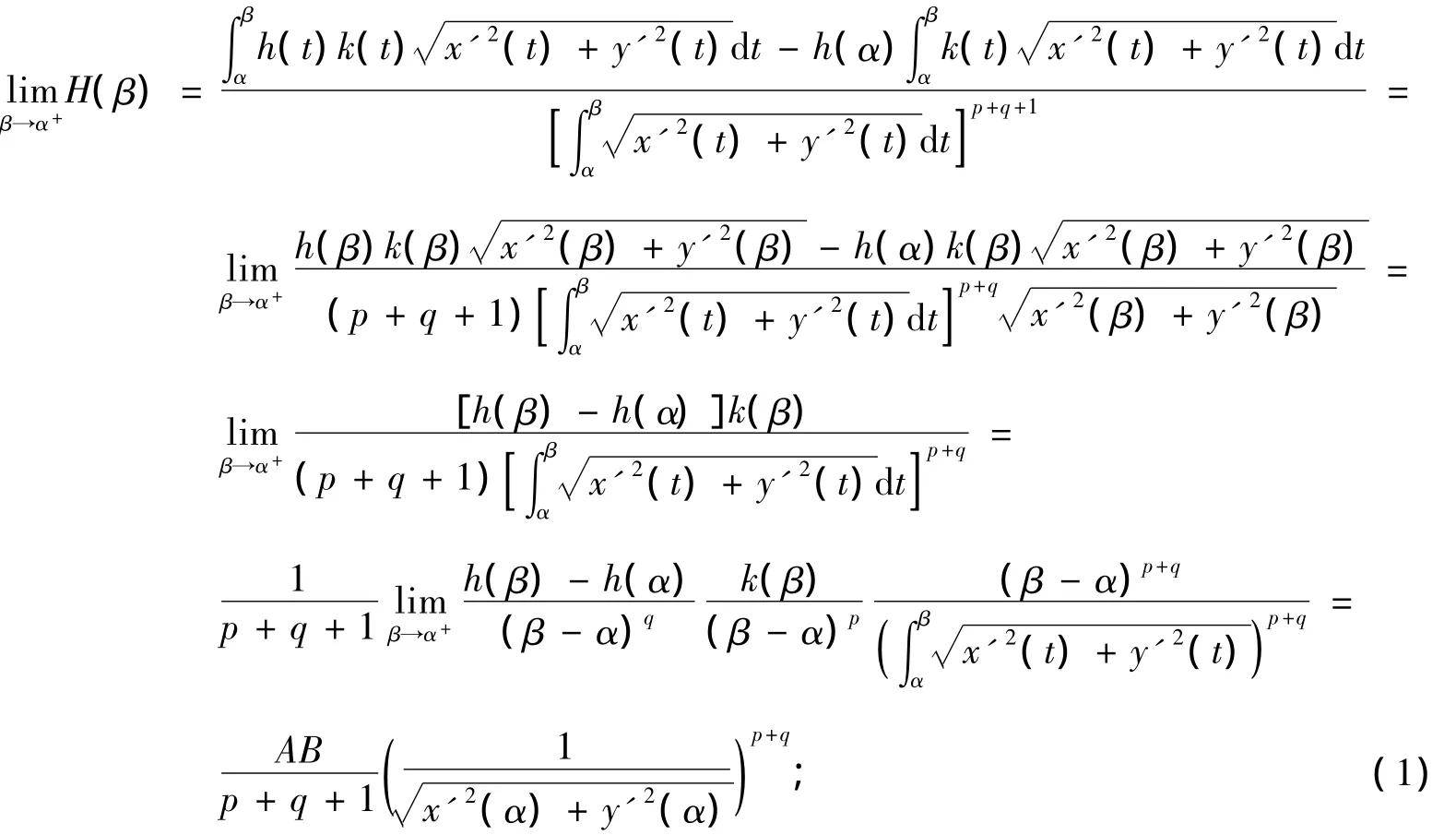
利用第一型曲线积分第二中值定理和L`Hospital法则，又得到

比较(1)式和(2)式，我们有

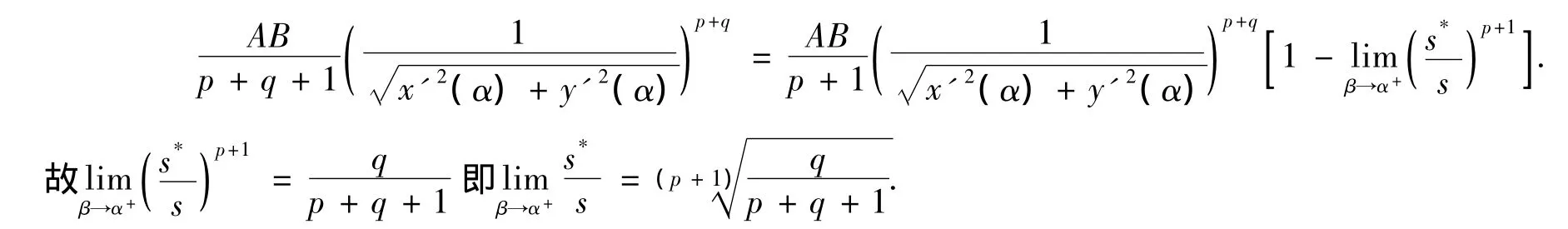
注:定理1中的“中间点”M［x(ζ)，y(ζ)］∈C(A，B)，s*，s分别是曲线C(A，M)和C(A，B)的长.上述的通式为,当时q=1，即其中实数p＞－1，则该通式可表示为，即当k(α)不为0其中q＞0，则通式可表示为;更特别的当q=1时，存在且不为0时，也即f(x，y)在当α的某领域存在一阶导，g［x(α)，y(α)］≠0，即

证明:考虑光滑曲线C(A，B):x(t)=t，y(t)=0(α≤t≤β)，在曲线C(A，B)上，g［x(t)，y(t)］=g(t)，f［x(t)，y(t)］=f(t由题意知，g(t)在［α，β］上连续可积，f(t)是［α，β］上单调连续曲线积分化为了区间［α，β］上的积分，即定理2中的

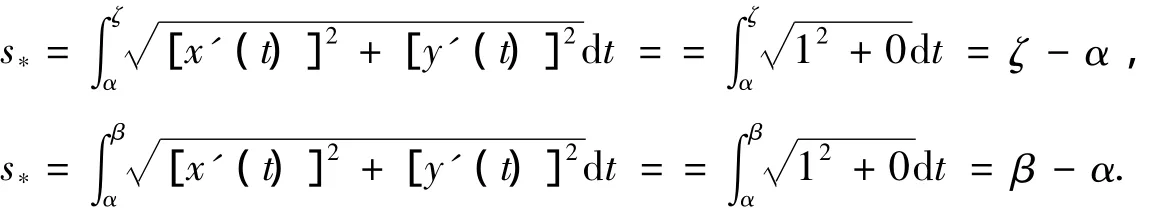
由定理2，可知积分第二中值定理的“中间点”ζ有渐近性

定理3如果曲线C(A，B):x=x(t)，y=y(t)(α≤t≤β)是光滑的，函数g(x，y)是曲线C(A，B)上的连续函数，f(x，y)是曲线C(A，B)上关于参数t单调的连续函数，并且h(i)(α)=0，(i=1，2，…，n－1)，hn(α)=0，k(m－1)(α)≠0，k(j)(α)=0(j=0，1，…，m－2)这里k(t)=g［x(t)，y(t)］，h(t)=f［x(t)，y(t)］，那么定理1中的“中间点M［x(ζ)，y(ζ)］∈C(A，B)有渐近性*，其中s，s分别是曲线C(A，M)和C(A，B)的长。

证明:由于函数h(t)=f［x(t)，y(t)］在点α处存在n阶导数，则函数h(t)在点α处带有Peano型余项的泰勒展开为

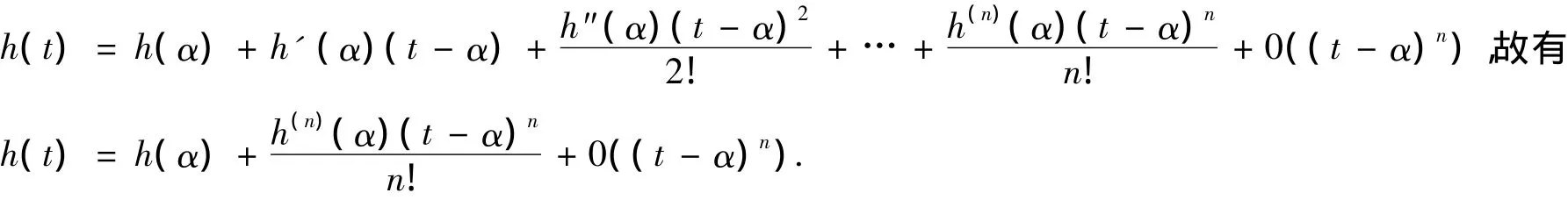
同理，函数k(t)=g［x(t)，y(t)］在点α处存在m－1阶导数，则函数k(t)在点α处带有Peano型余项的泰勒展开得到

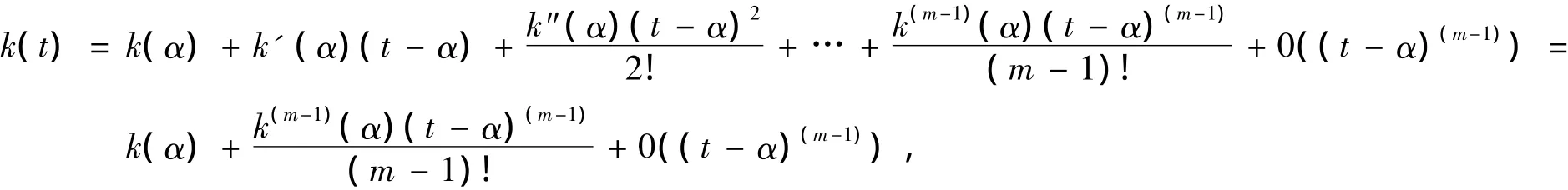
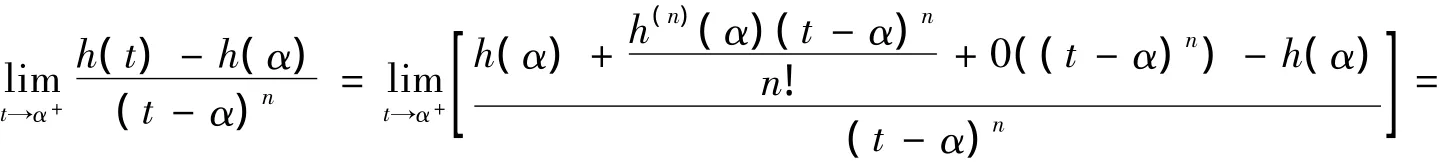
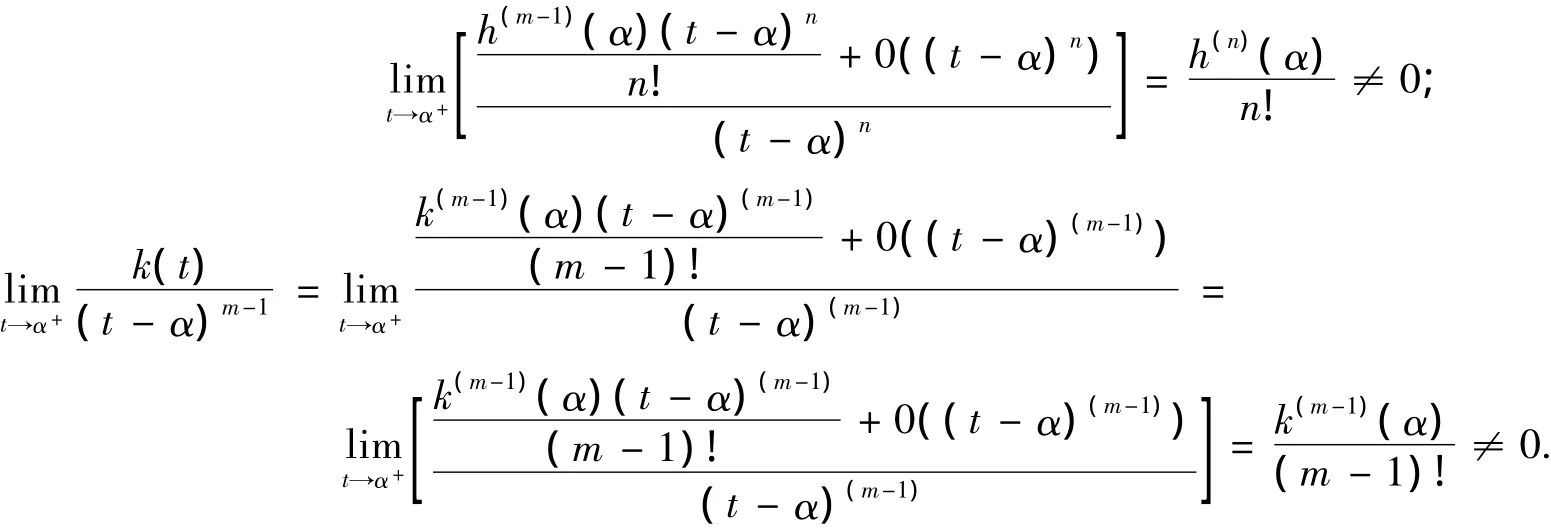
由定理2可知定理1中的“中间点”M［x(ζ)，y(ζ)］∈C(A，B)有渐近性，其中s*，s分别是曲线C(A，M)和C(A，B)的长。

注:定理1中的“中间点”M［x(ζ)，y(ζ)］∈C(A，B)，s*，s分别是曲线C(A，M)和C(A，B)的长.上述的通式，当n=1时，即f(x，y)存在一阶可导，g(x，y)存在直到m－1导时，该通式可表示当m=1时，即g(x，y)当β→α时连续不可导，f(x，y)存在直到n导时，即该通式可表示为

推论［1］若函数g(x)在［α，β］上连续且不变号，f(x)在［α，β］上单调且连续，fn(α)存在，且f(i)(α)=0(i=1，2，…，n－1)，f(n)(α)≠0，n≥1，g(m－1)(α)≠0，g(j)(α)=0，(j=0，1，…，m－2)，ζ是积分第二中值定理的“中间点”，则

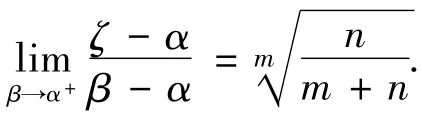
证明:考虑光滑曲线C(A，B):x=x(t)，y(t)=0(α≤t≤β)，在曲线C(A，B)上，g［x(t)，y(t)］=g(t)，f［x(t)，y(t)］=f(t)由题意知，g(t)在［α，β］上连续且不变号，f(t)在［α，β］上单调且连续，f(n)(α)存在，且f(i)(α)=0(i=1，2，…，n－1)，f(n)(α)≠0，n≥1，g(m－1)(α)≠0，g(j)(α)=0(j=0，1，…，m－2)

曲线积分化为了区间［α，β］上的积分，即定理3中的

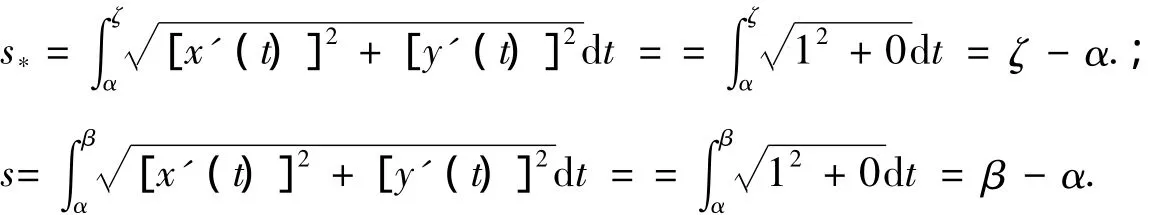
由定理3，可知积分第二中值定理的“中间点”ζ有渐近性

以上的推论是曲线积分第二中值定理“中间点”的渐近性在定积分第二中值定理“中间点”的渐近性的推广。

［1］吴俊，严平.关于第二积分中值定理中的渐近性［J］.安徽师范大学学报(自然科学版)，1999，22(2):111－113.

［2］吴至友，夏雪.积分第二中值定理中间点的渐近性［J］.数学的实践与认识，2004，34(3):170－176.

［3］刘文武.积分第二中值定理的一个一般性结果［J］.河南科技大学学报(自然科学版)，2005，26(5):90－92.

［4］华东师范大学数学系.数学分析(上册)(第三版)［M］.北京:人民教育出版社，2001.

［5］杨彩萍，贾云暖.关于积分中值定理的一个一般性结果［J］.数学的实践与认识，2002，32(4):670－698.

［6］郑权.积分第二中值定理的中间点的渐近性质［J］.大学数学，2005，21(6):113－115.

［7］张凤霞.曲线积分中值定理中间点的渐近性［J］.商丘师范学院学报，2001，17(4):107－109.

［8］裴东林.曲线积分中值定理中间点的渐近性的一个注记［J］.甘肃教育学院学报(自然科学版)，2003，17(4):13－15.［9］刘孝书.第一型曲线积分中值定理中间点的渐近性［J］.广西右江民族师专学报，2005，18(6):1－5.

［10］赵益坤，节存来，王磊.关于曲线积分中值定理中间点的一个一般性质［J］.大学数学，2007，23(1):166－169.

［11］菲赫金哥尔茨，ГМ.微积分学教程［M］.北京:人民教育出版社，1956.

［责任编辑刘景平］

On Asym ptotic Property of the Mid－point of the Second Mean Value Theorem for First Form Curve Integral

LIN Dong－cui
(Guangxi College for Preschool Education，Nanning，Guangxi530022，China)

The asymptotic property of themid－pointof the second mean value theorem for first form curve integral is investigated．Then the result is generalized to the asymptotic estimation for themiddle pointof the second integralmean value．This conclusion is derived from the corresponding results of the definite integral of the second mean value theorem．By using the first curve points，themean pointof the secondmean value theorem for first kind curve integral is discussed．Finally the conclusions in this article extend those in［1］，［2］and［3］．

first form curvilinear integral;mean value theorem;mid－point;asymptotic property;

book=0,ebook=21

O175

A

1672－9021(2012)02－0065－07

林冬翠(1977－)，女(壮族)，广西南宁人，广西幼儿师范高等专科学校公共基础部讲师，主要研究方向:理论数学。

2011－10－26