钴基合金激光熔覆覆层截形与显微硬度关系的调控研究
艾金山,李必文,程 强,何 彬,周 炬
(1.南华大学 机械工程学院,湖南 衡阳421001;2.衡阳技师学院 机械工程系,湖南 衡阳421101;3.南华大学 核科学技术学院,湖南 衡阳 421001)
以钴基合金作为核级阀门密封面材料可满足耐冲蚀、耐腐蚀、耐擦伤、耐磨损和高温红硬性的工况要求,可实现高安全性和可靠性。钴基合金的高温性能较镍基合金更好,很适于采用激光熔覆。研究表明,采用钴基合金粉末对核阀密封面进行激光熔覆时,熔覆道截形常呈半月形,如图1 所示。熔覆层由表及里存在硬度梯度,环形密封面熔覆道出现失圆和不平整的现象[1~3]。既要保证机在加工后得到足够宽的密封面尺寸,又要有理想的表面硬度值与之匹配,还要节约昂贵的钴基合金粉末,是核阀表面工程工作者亟待解决的问题。
1 实验材料与工艺
试件基体材料为0Cr18Ni12Mo3Ti 奥氏体不锈钢,化学成份(Wt%)为:C燮0.08,Si燮1.00,Mn燮2.00,S燮0.03,P燮0.035,Cr16~19,Ni11~14,Ti5 (C%-0.02)~0.80,Mo2.5~3.5,阀体零件如图2 所示,试样据阀体零件结构尺寸设计制作;自熔性合金粉末为长沙矿冶粉末冶金研究所研发的FCo-5,其化学成份(Wt%)及各元素的比热容、熔化潜热如表1 所列;粘结剂为2123 粉醛树脂粉,用分析醇稀释调合;激光加工机为TJ-HT-T5000 型5 kw 横流CO2激光器,多模输出;试件由多轴联动工作台驱动。粉末加入方法为预涂敷,在等厚度熔覆试验中,根据覆层高度在2~2.5 mm 范围内,进行预涂敷厚度的调整,在预涂层风干后,缓升至390~410 ℃,保温1.5 h;矩形光斑尺寸a×b=5×4 mm,光斑与工件的位置按图3 调节,以保证功率利用率。单道扫描,由于基于环形密封面熔覆道易失圆,试样密封面宽度单边放了0.3~1 mm的机加工余量;激光加工工艺规准为:激光功率P=2 800~3 200 w,扫描速度。

表1 FCo-5 粉末的成份及各元素的比热容、熔化潜热

图1 熔覆道截形示意图

图2 阀体零件图

图3 光斑与工件的位置调节

图4 激光熔覆结合区组织×1 000
2 实验结果的数学处理
2.1 熔覆道截形曲率半径数学模型的建立
图4 为得到良好冶金结合的某试样的金相图,其熔覆道截形体视图如图5 所示,呈半月形。用大型工具显微镜对该截形轮廓进行测量,以CAXA-WEDM 软件对测量所得系列特征点进行0.2 mm精度下的单圆弧曲线拟合,即可得到该试样熔覆道截形的曲率半径,如图6 所示。将所有试样熔覆道截形的曲率半径作为验证数学模型正确性的依据。

图5 熔覆道截形体视图

图6 熔覆道截形轮廓的单圆弧曲线拟合
文献[4]提出了基于同轴送粉方法的熔覆道截形曲率半径数学模型:

式中,
T0为熔池原始温度;
Tf为熔池最高温度;
Cp为熔覆材料的比热;
L 为熔覆材料的熔化潜热;
ν 为工件移动速度即扫描速度;
ρp为粉末的当量实体密度;
f 为熔覆材料对激光的吸收系数;
P 为激光功率。
该公式未能说明P 为激光器输出的总功率还是仅用于熔覆层的能量,而实际上加热基体达到表面熔化所需能量会比熔化粉末层所需能量大得多[5]。另外,通常认为,由于同轴送粉时激光可以直接照射到基体和粉末,粉末熔化时吸收系数高,熔化后的覆层表面吸收系数也高,所以送粉法所需的能量比预涂覆法要小。有基于此,本实验对式(1)进行了必要的修正,以保证其适用性。
加权考虑预涂覆粉末熔化时的吸收系数及粉末熔化后的覆层表面吸收系数,取熔覆材料对激光的吸收系数f 为0.55;按加热单位面积基体达到表面熔化所需能量的计算值,将激光器输出的总功率按比例合理分配到粉末和基体,约为0.148:0.852,即式(1)中的P 修正为k1P = 0148P,单位为w;T0按预热温度取为400 ℃,Tf经红外测温仪测得为2 600 ℃;Cp为自熔性钴基合金粉末FCo-5 的定压比热容,采用加权平均法公式Cp = (M1C1+M2C2+…+MnCn)/(M1+M2+…+Mn)计算,得Cp为453.12 J/kg.k;同理,熔化潜热L 为502.70 J/g;ρp取为8.2 g/cm3。
基于预涂覆法的熔覆道截形曲率半径数学模型为:

以图5 试件为例,当P=3 000 w,ν=2.8 mm/s 时,在0.2 mm 精度下拟合出的单圆弧半径为2.69 mm,而按式(2)的计算值为2.61 mm,相对误差仅为2.97%。本实验对10个试样的熔覆道截形轮廓进行了数学处理,相对误差在3.6%以内。
2.2 显微硬度分布曲线数学模型的建立
用HXD-1000B 型维氏显微硬度计对熔覆层、结合层及基体热影响区进行硬度测试,基于各试样的统计数据,得到图7 细实线所示的显微硬度分布曲线。为使所建模型精确且具实用价值,本研究采用二维曲线拟合与经验公式查找软件TableCurve 2D,综合考查了1.94 mm 等厚度熔覆时,基体以上显微硬度分布曲线各拟合结果的剩余标准误差、相关指数、连续性、光滑性、保形性及拟合误差等因素,得到了迭代拟合的标准有理式数学模型:

式中,
H 为维氏硬度值;
h1为机加工切除的圆弧弓高尺寸。
基体以上显微硬度分布拟合曲线,如图7 所示虚线。
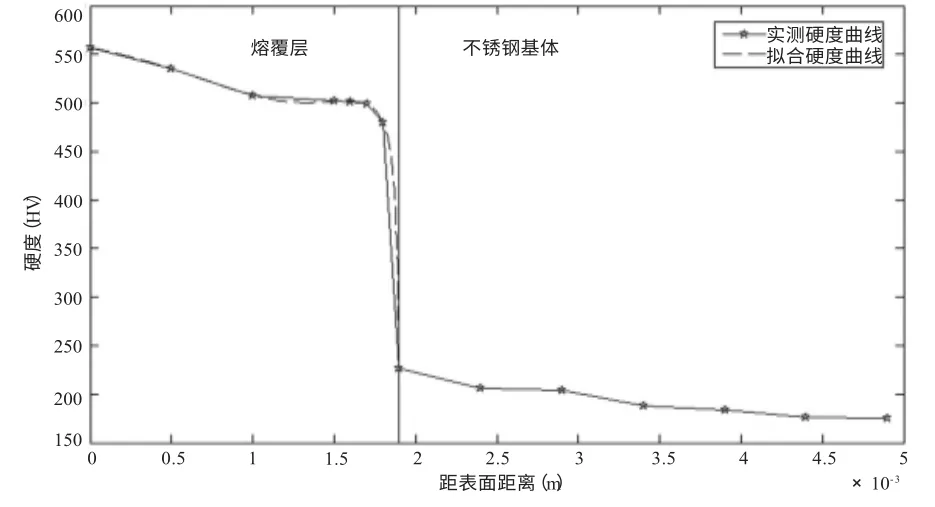
图7 显微硬度分布曲线及其基体以上部分的拟合曲线
3 覆层截形与显微硬度关系调控的优化设计模型
进行覆层截形与显微硬度关系的调控,是为了机加工在切除圆弧弓高尺寸h1及密封面宽度余量2δ 后(参见图1),得到所需的理想表面硬度值H,且熔覆粉末材料用量最省。
对熔覆道截形建立曲率半径的数学模型后,其截面积s 与曲率半径ra、熔覆道工艺宽度l 的关系为:

其中,l 为密封面最终宽度l0加双边机加工余量2δ,且基于熔覆厚度h0与激光功率成正比、与扫描速度成反比的事实,可建立关系式:

在h0=1.94 mm 等厚度熔覆的条件下,已知k1=0.148,可求得k1=0.012。
由于ra、h0均为P、ν 的函数,故可认为:

h1与l0、ra的关系为故可认为:

又因h1与H 有式(3)的关系,故可认为:

综合以上关系,本优化问题可归结为有约束非线性最优化问题,目标函数为熔覆道截面积s,设计变量为激光功率P 及扫描速度ν,且均可为连续变量。描述为:

利用MATLAB 最优化工具箱进行求解。运行程序,动态给定l0的值之后,可得到目标函数s →min时,l、P、ν、h0、ra、s、H 的值。由于阀门阀体密封面与阀盖密封面应存在合理的硬度差,所以H 即f5(P,ν)的上、下限可根据实际需要来调整确定。本研究优化程序是按输入密封面的洛氏硬度值而编制的,以免除人工换算成维氏值的麻烦;H 的HRC 值范围可在源程序中更改,亦允许动态给定。例如当输入l0=3 mm时,得到的优化结果如表2 所示。

表2 优化结果
4 结束语
本研究提出在对核阀密封面进行钴基合金粉末激光熔覆时,密封面熔覆道宽度一定要设计工艺尺寸。在建立熔覆道截形曲率半径的数学模型、熔覆层显微硬度梯度分布的数学模型及理清密封面几何参数、机械性能参数与激光加工参数关系的基础上,构建了等厚度熔覆条件下粉末用量为目标函数的优化设计模型,实现了覆层截形与显微硬度关系的调控。这对于激光熔覆的研究和生产具有一定的理论价值和指导意义。
[1]闫毓禾,钟敏霖. 高功率激光加工及其应用[M]. 天津:天津科学技术出版社,1994.
[2]郑启光,等. 激光热加工[M]. 武汉:华中理工大学出版社,1995.
[3]李必文,石世宏. 激光熔覆化工阀门的实验与质量控制研究[J].热加工工艺,2000,(1):30-31.
[4]J.mazumder,A.Kear.Solid Solubility in Laser Cladding.J.of Metal,1987,(2):24.
[5]路有勤,郭 伟.激光熔覆温度场的研究现状[J].山西机械,1999,(3):36-38.

