基于转矩观测的分时换相策略的无刷直流电机直接转矩控制
冯嘉鹏, 王喜顺
(华南理工大学机械与汽车工程学院,广东广州 510642)
设电机在t=0时换相,此时,AC相之间的电压由Ud变成0,BC相之间的电压由0变成Ud。设在t=toff时刻A相电流由I变为0,而B相电流由0变为iB(toff),而此后变化到稳定值I。即有iA(0)=I,iB(0)=0,iC(0)= - I。令 L=LS- LM,对式(1)进行拉普拉斯变化并代入初始条件,得到在区间[0 toff]内的电流方程为
同理,当t>toff时的电流方程为
0 引言
直接转矩控制(Direct Torque Control,DTC)是由德国学者 M.Depenbrock和日本学者 I.Takahashi首先针对异步电机提出的一种先进的标量控制技术[1-2]。其基本原理是将电机的定子磁链和转矩的观察值与理想值相比较,再根据结果通过查表的方式选择最优的电压空间矢量,实现对转矩的直接控制,其难点在于磁链轨迹的观测与给定。文献[3]首次设计了带磁链观察环节和转矩观察环节的DTC。但是所采用的转矩观察公式中包含两个微分量,不但计算量大,而且易产生较大的误差。文献[4-5]通过分析认为二二相导通的无刷直流电机(Brushless DC Motor,BLDCM)换相转矩波动产生的其中一个重要原因是关断相的存在,从而提出一种三三导通的直接自控制策略。同时,针对传统转矩观察公式含有微分量,采用了通过构造反电动势函数的方法计算转矩,从而减小计算量,提高观察精度。
最佳分时换相策略是通过在二二相导通方式的换相期间适当地插入三三相导通方式来补偿由于换相电流下降带来的转矩下降,其难点在于最佳分时时刻和各相导通时间长短的确定。文献[6]分析了换流过程给转矩波动带来的影响,给出了一种选择理想换相时刻的方法,就是通过测量反电动势的大小并与电路总电压作比较,当符合某一确定的比例关系时进行换相能保证转矩不变。但该状态下的电机处于加速阶段,难以维持该状态。文献[7]通过分析换相时反电势和换流过程对转矩波动的影响,提出了分段控制办法,在换相不同的时刻利用PWM的方式实现三相混合导通,以抑制转矩波动。但是由于换相期间分段的依据是假设电流线性变化而推导的,与实际有一定的误差,而且最后PWM的占空比计算公式较为复杂。
本文结合最佳分时换相策略和DTC的优点,用分时换相策略代替磁链观察环节,同时将直接转矩中的转矩观察用于分时换相时刻与分时时段长度的确定,设计出一种结构简单,实用性强的BLDCM控制系统。仿真试验结果表明,该系统在电机高速或低速运行时都能达到良好的转矩波动抑制效果。
1 BLDCM模型与电压方程
三相星型连接的BLDCM控制电路如图1所示,电压方程可用式(1)表示[8]:
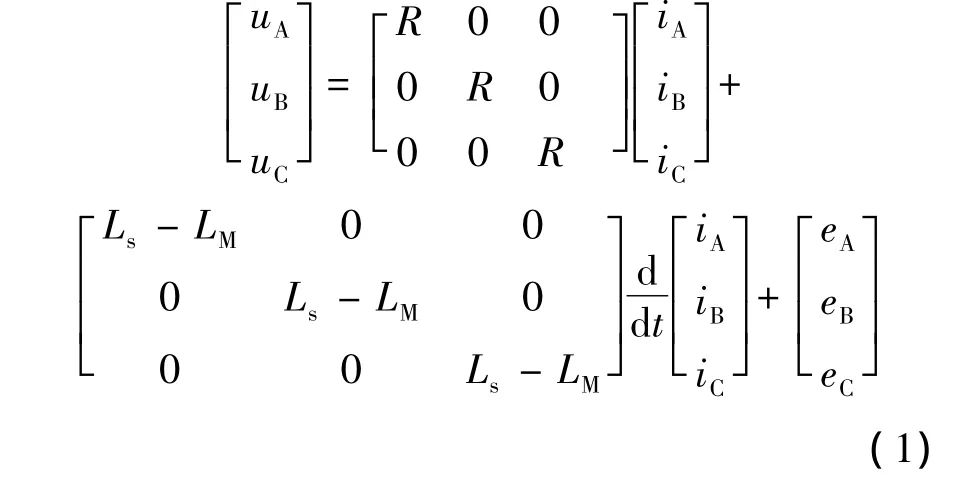
式中:uA、uB、uC——三相输入电压;
eA、eB、eC——三相电动势;
iA、iB、iC——三相电流;
Rs、Ls、LM——定子每相绕组的电阻、自感、定子任意两相绕组间的互感。
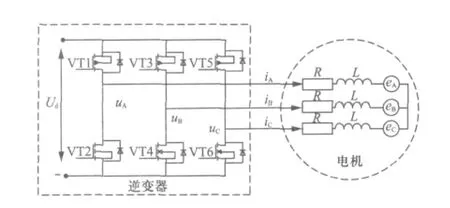
图1 三相全桥连接BLDCM控制电路
2 换相时换流过程对转矩波动的影响
忽略PWM控制和反电势波形变化的影响,设相反电势在换相期间保持不变,均为稳态值E或-E,则稳态时导通相的电流I稳定为
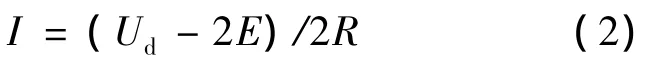
由于绕组电感的作用,在换相时电流不能突变,以AC相导通转换到BC相导通的换相过程为例作分析,换相可能是上半桥换相或者是下半桥换相,其等效电路结构一致,只是电流流向相反,故,以上半桥换相为例作分析,等效电路图如图 2所示。在区间[0,t1]内电磁转矩为
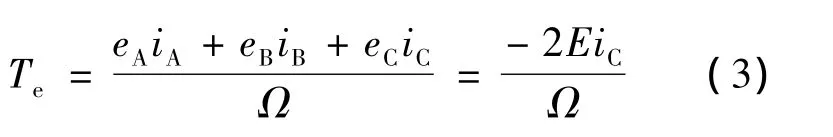
式中:Ω——电机机械角速度。
由式(3)可知,在不考虑反电动势波动影响的情况下,换相时转矩波动由关断相电流决定,如上例中的电流iC。这也就是说通过分析关断相电流在换相期间的变化就可以知道转矩的变化。

图2 无刷直流电机上半桥换相过程等效电路
2.1 二二相导通方式换流过程对转矩的影响
设电机在t=0时换相,此时,AC相之间的电压由Ud变成0,BC相之间的电压由0变成Ud。设在t=toff时刻A相电流由I变为0,而B相电流由0变为iB(toff),而此后变化到稳定值I。即有iA(0)=I,iB(0)=0,iC(0)= -I。令L=LS-LM,对式(1)进行拉普拉斯变化并代入初始条件,得到在区间[0toff]内的电流方程为
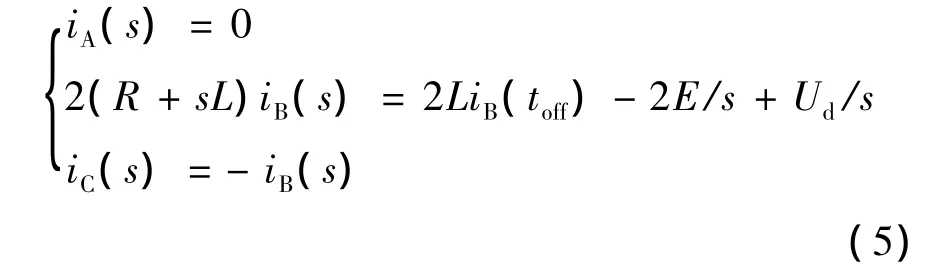
同理,当t>toff时的电流方程为
求出式(3)和式(4)的时域解,并把式(2)代入得

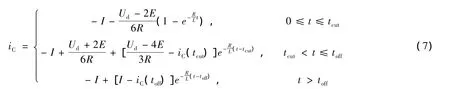
由式(6)可知在[0toff]区间,ic的幅值单调减少,而当t>toff时,ic幅值由iC(toff)单调增加到稳态值I,但在整个期间ic的幅值都小于稳态值。因此,对于二二相导通方式,由式(3)可知,换相期间的电磁转矩始终小于稳态值,也就导致了电机运行期间的转矩波动。该节公式具体推导过程可参考文献[9]。
2.2 二三相混合导通方式换流过程对转矩的影响
同样以AC相导通转换到BC相导通为例进行分析,设在ton时刻,开通B相,在tcut时刻关闭A相,且iA(toff)=0。采用二三相混合导通方式是指在换相期间通过提前导通关断相的方式来补偿转矩的下降,即满足ton<tcut<toff,同理可得换相期间的电流方程,并求得时域解为
由式(7)可知,在[0tcut]期间,iC的幅值由稳态值I单调增加到iC(tcut),而在[tcuttoff]期间开始回落,当t>toff时又开始由iC(toff)上升到稳态值I。由此可知,当换相期间提前导通关断相会使iC的幅值有一个增加的过程,也就使电磁转矩相应增加。如果通过适当的控制,在二二相导通方式换相期间适时地插入三相导通方式,补偿由于换相所带来的转矩下降,就可以有效抑制转矩的波动。但同时也产生一个问题,就是三相导通状态应该在换相期间什么时刻插入和插入时间的长度。DTC当中的转矩观察环节能为解决该问题提供一个途径。值得注意的是,在前面的分析当中,是假设反电动势是理想的120°梯形波,但实际相反电动势平顶宽度通常小于120°,这也会导致换相期间转矩的下降[10]。但设计的方法是基于最终电磁转矩的观察结果为依据分时换相的,其本身就包含了对非理想电动势带来转矩下降的补偿。
3 基于转矩观测二三相混合导通的DTC
DTC方法的基本思路是通过分析得出电机运行时的磁链轨迹模型,然后将实际观察得到的磁链值与磁链轨迹模型相比较,得出磁链的误差信息。同时,也将观察得到的转矩值与给定值相比较,得出转矩的误差信息。最后依据这两种信息在预先制定好的矢量表中得出最优的电压空间矢量[11]。在实际应用中,一方面电机由于存在绕组漏磁等现象,实际磁链轨迹与理想模型有一定的差距;另一方面磁链不能直接观察,只能通过相电流、相电压和转速等间接计算得到。这就会使最终得到的磁链误差信息失真。在此基础上,本文省去磁链观察环节,将转矩观察得到的误差信息用于电机换相时判断插入三相导通状态的时刻和插入时间长度,实现补偿换相期间转矩的下降,达到抑制转矩波动的目的。同时由于省去了磁链观察环节,降低了系统的复杂程度,实用性更强。
3.1 转矩观察环节
早期的文献多通过磁链来计算转矩,但由于磁链观察误差较大,以及该类计算公式都包含了微分量,所以不但计算量大,而且易引起较大的误差。随着对无刷直流电机研究的深入,提出了通过构造反电动势函数的方法来估计反电动势。从这以后的文献多采用直接从转矩的定义式(3)出发,通过三相反电动势和三相电流计算电磁转矩。
由式(3)可知,要计算电磁转矩,除了要测量三相电流的值以外,还要测量反电动势的值。但是直接测量反电动势是很困难的。反电动势法是先通过检测BLDCM运行时梯形反电动的平顶段的起点与终点的角度差值x,然后依此构造出三个相位互差120°,幅值为1,平顶宽度为x的形状函数,如图3所示。对于BLDCM,平顶宽度x可通过位置传感器的信号来实现。
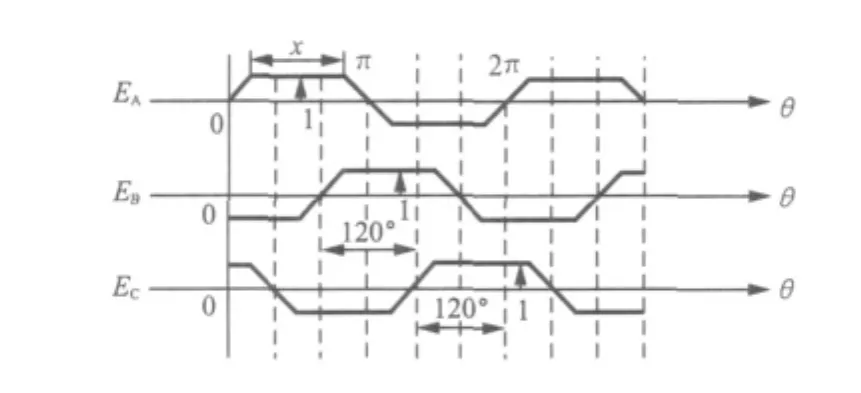
图3 反电动势形状函数
反电动势函数的平顶宽度为x,梯形斜边的斜率为k=2/(π-x),三相反电动势函数用分段函数的方式可表示为
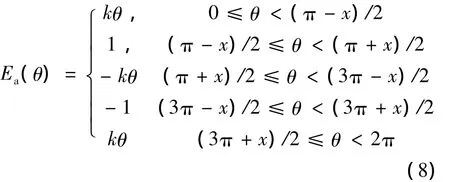
同理利用三相反电动势的关系Eb(θ)=Ea(θ-2π/3),Ec(θ)=Ea(θ+2π/3)求得。
容易知道BLDCM梯形反电势的幅值正比于转速n[12],有以下公式:
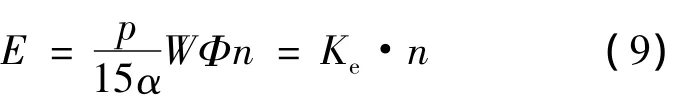
式中:p——极对数;
α——计算极弧系数;
W——每相绕组有效串联匝数;
Φ——每极磁通;
Ke——反电势系数,均为常量。
联合式(8)和式(9),有
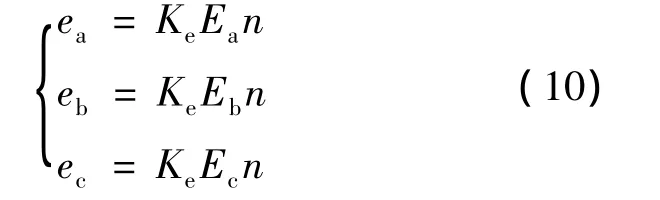
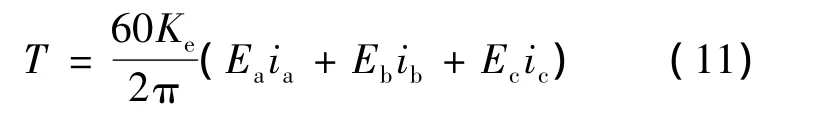
3.2 控制开关表
开关表的作用是根据转矩的误差信息和转子的位置信息选择最优的电压空间矢量。转子的位置信息可通过位置传感器测量,它主要是为开关表提供转子所在扇区的信息。将转子旋转一圈(假设极对数为1)分成六个扇区(S1—S6),每个扇区占60o,如图4所示。对于二二相导通方式,逆变器上下桥六个功率开关有六种开合组合。同样,对于三三相导通方式也有六种开合组合。本文采用六位二进制数表示功率开关的开合状态对应的电压空间矢量,其中1代表功率开关导通,0代表功率开关不导通。例如当VT1、VT6导通时,AC相导通,B相不导通,电流从A想绕组流入,从C相流出,产生的合成电压空间矢量就表示为U1(100001)。同理对于二二相导通方式有VT2、VT3、VT4、VT5、VT6;对于三三相导通方式有 VT61、VT12、VT23、VT34、VT45、VT56;具体如图4和表1所示。表中T*为转矩的给定值,T为转矩观察值,ΔT为误差的控制范围,U0(000000)为零矢量。BLDCM控制系统根据转矩误差的信息和位置信息(扇区),在开关表中选择最优电压空间矢量,不但可以实现正确的换相,同时可以适时抑制转矩波动。
将式(10)代入式(3)得

表1 控制开关表
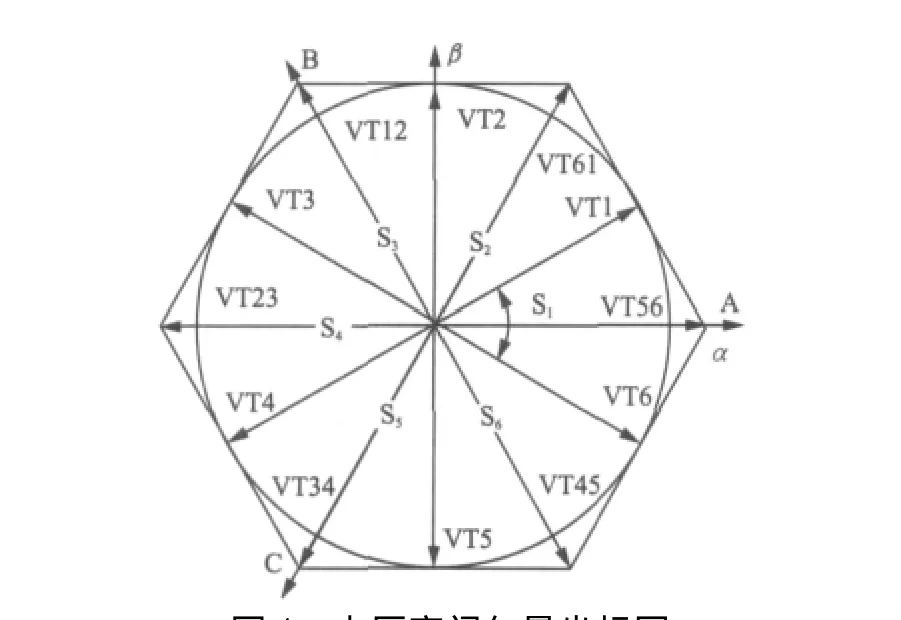
图4 电压空间矢量坐标图
4 仿真与试验
基于转矩观测二三相混合导通的BLDCM的DTC结构如图5所示。在MATLAB/Simulink上建立仿真模型。仿真用的电机参数具体如下:极对数4;额定电压24 V;额定转速4 000 r/min;保持力矩0.063 N·m;反电动势系数4.4 V/krpm;线电阻 1.8 ohms;线电感 0.54 mH;转矩常数0.042 N·m/A;转动惯量 24 g·cm2。本文针对不同的给定条件分别进行两次仿真试验,第一次试验针对高转速情况,给定条件是:二二相导通方式起动,给定转速为2 000 r/min,空载起动,在0.015 s时刻突加转矩0.15 N·m,在 0.03 s时刻转变为二三相混合导通方式,在0.05 s时刻结束试验。相电流曲线、转矩曲线和速度曲线分别如图6、图8、图10所示。第二次试验针对低速场合,给定条件是:二二相导通方式起动,初始给定转速为200 r/min,空载起动,在0.2 s时刻突加转矩0.15 N·m,在0.4 s时刻转变为二三相混合导通方式,在0.5 s时刻结束试验。相电流曲线、转矩曲线和速度曲线分别如图7、图9、图11所示。

图5 控制系统结构图
通过仿真的结果,得出如下特点和规律:
(1)由图6、图8可看出,电机突加转矩后,采用二二相导通方式时,电机在换相期间电流下降严重,达到稳态值的40%,这导致了转矩下降为稳态值的40%,仿真结果与前文分析一致。当采用基于转矩观测的二三相混合导通方式时,由于提前导通了关断相,换相转矩下降得到了补偿,转矩的波动降为稳态值的5%。
(2)由图10可看出,突加转矩后的速度在额定值范围内波动,范围达±20 r/min。当采用二三相混合导通方式时,速度的波动明显下降,波动范围为±4 r/min。
(3)由图7、图9、图11可看出,在低速运行时,二三相导通方式同样达到了抑制转矩波动的效果,相电流、转矩分别降低到稳态值的4%和3%,速度波动范围为±3 r/min。在低速运行场合,该方法对系统转矩波动的抑制更加有效。
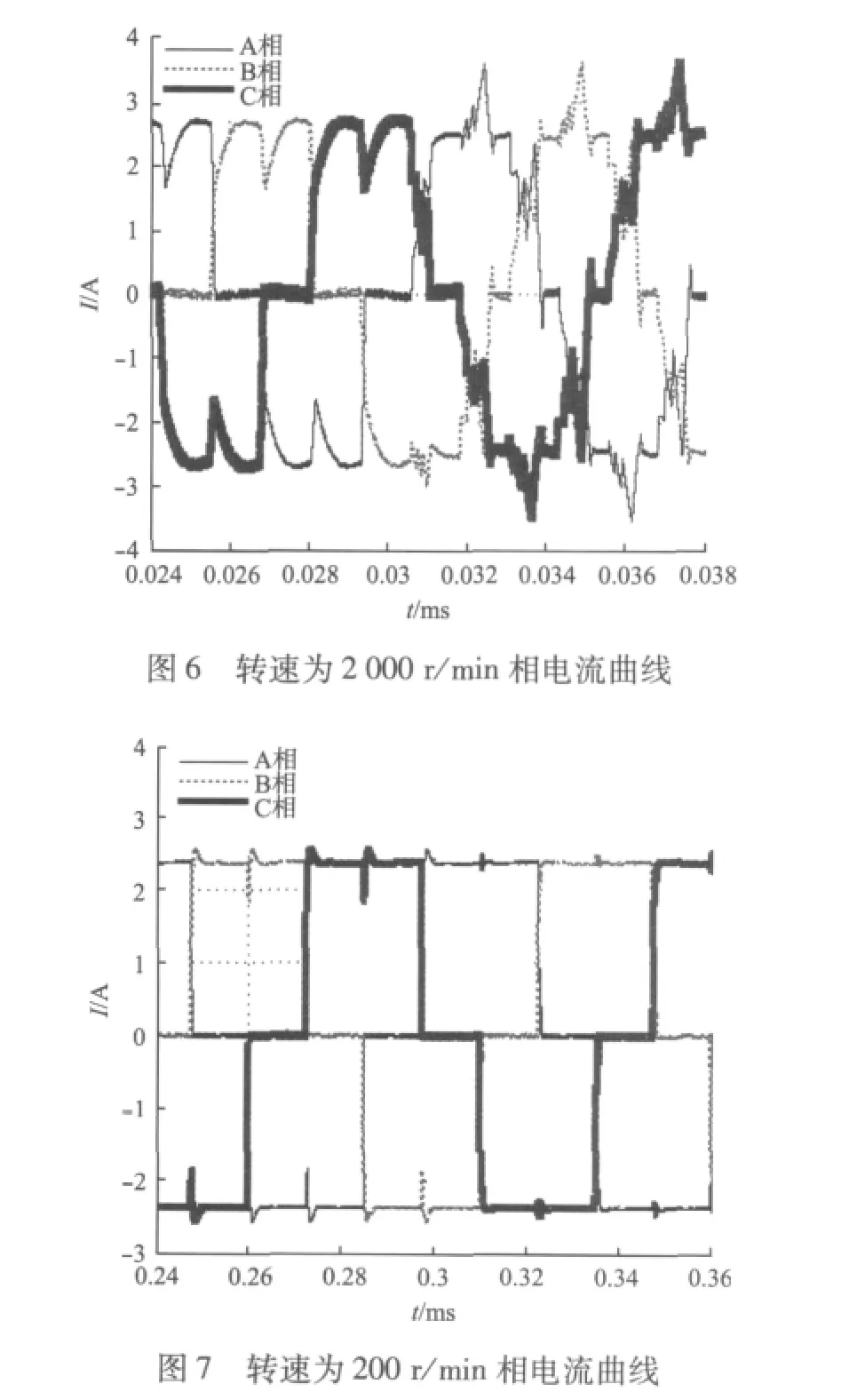
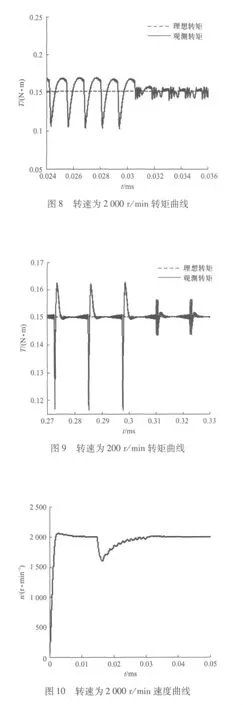
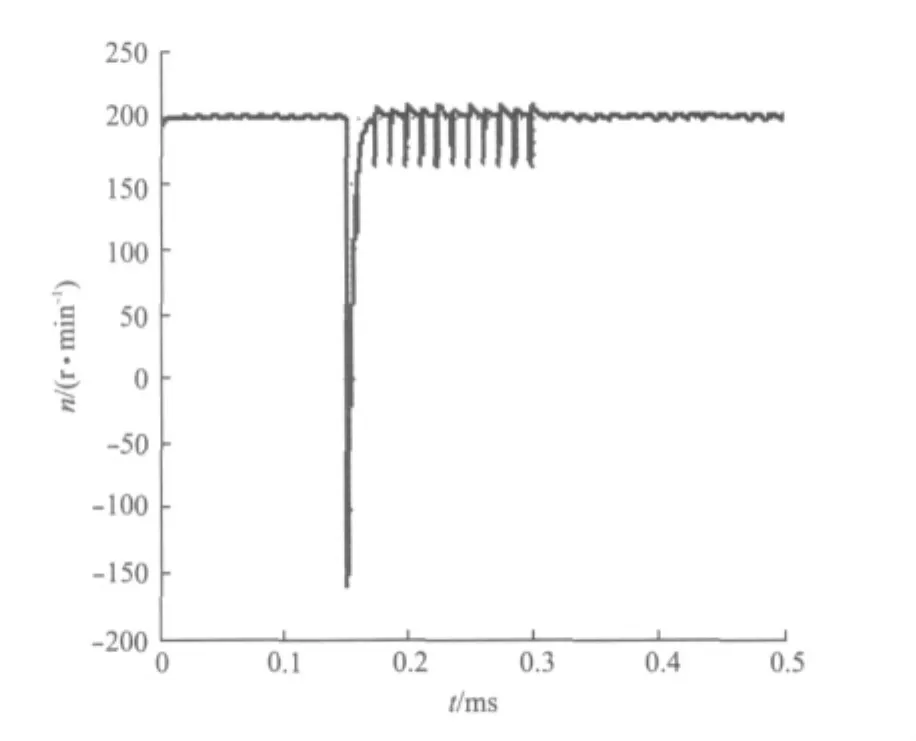
图11 转速为200 r/min速度曲线
5 结语
(1)二二相导通方式BLDCM在换相期间会产生转矩的下降,通过提前导通关断相能补偿转矩的下降;
(2)基于转矩观测的二三相混合导通方式的DTC不但能有效抑制转矩波动,而且结构简单,实用性强;
(3)本文设计的方法在低速运行场合同样有良好的效果。
本文基于简化DTC系统使其更适合实际应用的目的,设计出一种基于转矩观测的二三相混合导通方式的DTC系统,仿真试验结果表明,该系统不但能有效抑制电机的转矩波动,而且结构简单,易于实现,为DTC的实际应用提供了一条有效的途径。
[1]DEPENBROCK M.Direct self-control(DSC)of inverter-fed inductionmachine[J].IEEE Trans Power Electro,1988,3(4):420-429.
[2]BAADER U,DEPENBROCK M.Direct self control(DSC)of inverter-fedinduction machine:a basis for speed control without speed mesurement[J].IEEE Trans on Ind Application,1992,28(3):581-588.
[3]LIU Y,ZHU Z Q,HOWE D.Direct torque control of brushless DC drives with reduced torque ripple[J].IEEE Trans on Ind Application,2005,41(2):599-608.
[4]YANG J F,HU Y W,HUANG W X,et al.Direct torque control of brushless DC motor without flux linkage observation[J].IEEE2009 IPEMC,2009:1934-1937.
[5]高瑾,胡育文,黄文新,等.六边形磁链轨迹的无刷直流电机直接自控制[J].中国电机工程学报,2007,27(15):65-69.
[6]CARLSON R,LAJOIE M M,FAGUNDES J C S.Analysis of torque ripple due to phase commutationin brushless DC machines[J].IEEE Trans on Industry Application,1992,28(3):632-638.
[7]李怀兵,丑武胜,张延超.换相期间无刷直流电机转矩脉动的抑制策略[J].电机控制与应用,2011,38(11):20-24.
[8]阮毅,陈维钧.运动控制系统[M].北京:清华大学出版社,2006.
[9]夏长亮.无刷直流电机控制系统[M].北京:科学出版社,2009.
[10]张磊,瞿文龙,陆海峰,等.非理想反电势无刷直流电机转矩直接控制方[J].清华大学学报(自然科学版),2007,47(10):1570-1573.
[11]丁祥.永磁直流无刷电机直接转矩控制系统的设计研究[D].长沙:湖南大学,2009.
[12]李钟明,刘卫国.稀土永磁电机[M].北京:国防工业出版社,2001.

