2012年平面向量高考热点问题剖析
☉江西省于都中学 谢志斌
2012年平面向量高考热点问题剖析
☉江西省于都中学 谢志斌
通过新题或通过改变陈题的背景材料,来考查学生的能力是高考命题的常用方法.可与平面向量结合的知识点较多,如平面几何、立体几何乃至圆锥曲线、直线与方程等都能与平面向量进行交汇命题.求解这类题,需要学生具有扎实的数学基础和灵活运用数学基本思想方法的能力,并能在试题中提取有用的信息,进行加工整理.本文对今年高考中平面向量的热点问题进行分析,希望对读者能起到抛砖引玉的作用.
一、平面几何中考查平面向量

图1

分析:此题考查平面向量基础知识,目的是利用向量的工具性作用来解决向量的数量积问题.初看好像不好入手,但根据填空题的特征,不妨联想到特殊的正方形,问题便可迎刃而解!

再分析:是不是答案18只对正方形才会有呢?在一般的平行四边形ABCD中,结论又如何?
我们再去深思、去探索、去归纳.
解法2:(小题小做)设AC的中点为O,延长AP,过点C作其垂线CE,垂足为E,则OP是△ACE的中位线,由AP=3知AE=6.

点评:本题巧妙运用图像的特殊性求解,体现了平面向量“形”的特征.
二、动态中考查平面向量


图2
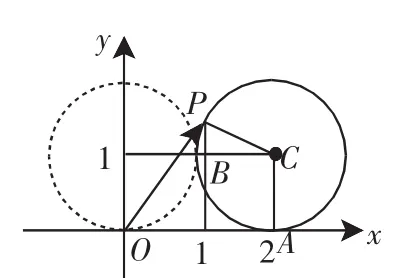
图3
分析:本题表面上是考查向量的坐标运算,实际上考查的知识点包含了弧度数、解三角形知识.解决本题的关键是根据圆心的运动坐标,确定点P的弧度数,从而确定∠PCA=2.

点评:本题是在运动中考查平面向量、三角函数、圆的知识,解决本题的关键是明确点P运动的弧度数为2,利用图形中特征直角三角形并结合诱导公式、向量坐标运算等知识处理.
三、交汇处考查平面向量


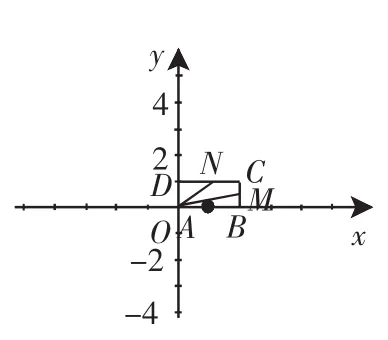
图4
点评:本题主要考查平面向量的基本运算、概念、平面向量的数量积的运算律.做题时,要切实注意条件的运用.本题属于中档题,难度适中.


图5
分析:根据所给的图形,把已知向量用矩形的边所在的向量来表示,做出要用的向量的模长,表示出要求的向量的数量积,注意应用垂直的向量的数量积等于0,得到结果.

点评:本题考查向量的计算,矩形的性质,三角形外角的性质,两角和的余弦公式,锐角三角函数的定义.
四、创新题中考查平面向量

解析:本题考查平面向量的数量积的运算以及向量的新定义,突破口是通过新定义把问题转化为熟悉的问题解决.根据新定义得:

点评:这类考题要求考生在阅读理解的基础上及时捕捉和利用信息,结合原有所学知识作出判断、推理、概括、运算和表述.这类题型背景新颖,构思精巧,极富思考性和挑战性,因而备受各级各类考试命题者的青睐.
解决向量热点问题可归纳概括为:两个基本点、一个重点、三个看点.具体地说,两个基本点主要是线性运算和坐标运算.对此必须牢固掌握、熟练运算;向量的数量积则是一个重点,决不能轻视;向量问题所呈现的三种情景:一是与平面图形交汇,二是与三角交汇,三是在物理中的应用.这三种情景便是三大看点,它体现了向量良好的工具功能、简化功能和综合功能.

