谈高三数学复习如何有效突破“瓶颈”

☉江苏省南通第一中学 刘新春

谈高三数学复习如何有效突破“瓶颈”

☉江苏省南通第一中学 刘新春

学生步入高三，复习了一段时间后，发现要想再有所提高则非常费力，学习遇到了“瓶颈”，传统的做法是搞题海战术，其结果是学生苦不堪言，效果也不是很好，本文从问题的创设和解题反思两个角度谈谈高三数学复习应如何有效地突破“瓶颈”.

一、合理设置问题，增强课堂复习的紧凑感

1.问题的设置应具有层次感

案例1：笔者在和学生一起探究求函数值时，从学生的最近发展区出发，考虑到所教班级的实际情况，设计了一个具有梯度的问题.

小步子、多台阶设置问题是近些年教学中常用的问题处理方式，不过，有一个误区值得我们一线教师注意，就是在拆解教学目标时，步子不能过细，因为问题过于琐碎了，势必将教学从满堂灌导向另一个误区——满堂问，如果满堂问，学生就很容易在琐碎问题中迷失，被问题牵着鼻子走，思维无法发散.

2.理答时注重问题的追加

案例2：笔者在和学生一起推导等差数列前n项和时，首先设置一个问题让学生思考.

学生调用原有的数学知识，将高斯算法迁移过来，进而快速地得到等差数列前n项和为Sn=（a1+an）+（a2+an－1）+…学生得到答案，大多认为问题已经完美解决.笔者看到这种情况，没有道破，只是进一步追加了问题引发学生深层次的思考.

追问1：大家得到上面的答案，是否考虑到了n的奇偶性？

笔者这样一问，学生瞬时注意到了思维的片面性，重新陷入了思考之中，分n为偶数和奇数重新进行求解，在一番思考和解答后，新的发现产生了：

追问2：在初中，“一个上底为a，下底为b，高为h的梯形，面积S的大小是如何推导的？”试着从梯形面积公式的推导方法迁移过来，试着在推导等差数列前n项和既可以用到首尾配对的高斯算法，又不受项数奇偶性的限制？

如此地追问实际是点拨学生的思维，学生联系到梯形面积公式的推导，将其大脑中的记忆表象提取出来，倒序相加的方法的生成就显得自然而不突兀了.

二、注重解题方法的引导和解题后的反思

1.关注学生的解答

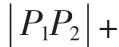
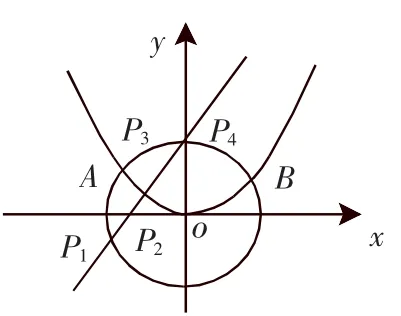
图1

从学生的作业情况来看有4种情况.

（1）反应无从下手，所以交了空白作业.

（2）能够具体计算出P1、P2、P3、P4四个点的坐标.

了解学生的解题实际，才会让我们的习题评讲和复习做到有的放矢，同时一定要帮助学生进行思维的训练，引导学生从概念最为本质的东西出发进行思考.

2.用问题引导学生反思

高中数学具有很强的系统性，数学各章节之间存在着较强的联系，把握知识之间的内在联系，引导学生从各个章节出发思考问题，既可以有效地开拓解题思路，又可以实现多章节的整体复习.

案例4：笔者在和学生一起探究如下问题时，引导学生从多个角度进行了思考.

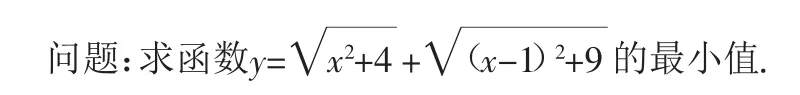
思考1：单纯从代数解法去考虑，将表达式移项、平方、整理成关于x的二次方程，会找到利用判别式Δ≥0的解法.

思考2：用导数法来解，利用复合函数的求导公式.

思考3：观察函数解析式的形式，联想解析几何中两点间的距离公式，建立直角坐标系，求x轴上一动点P（x，0），使它到点A（0，2）、B（1，3）的距离之和为最小.依据“异侧和最小，同侧差最大”去求解.

3.注意逆向思维训练

案例5： 已知三条抛物线y=x2+4ax+3，y=x2+（a－1）x+a2，y=x2+2ax－2a之中至少有一条与x轴相交，试分析实数a的取值范围.

解析：对于这个问题，从一般的思维习惯出发，需进行分类讨论，利用等价性进行求解，相当复杂，将命题进行转换，思考“三条抛物线均与x轴无公共点时a的范围”，然后再求其补集，那么思维就容易多了，这也是最为常见的数学思维方式，在复习时要注意渗透.

三、结束语

高三复习不是简单的知识回顾和做题的过程，需要我们教师投入更多的精力去探索适合所教班级学生的复习方法，只有从学生的实际出发进行问题设置和引导，复习才会走向高效.