在反思中探究,在探究中反思：“以某线段为直径的圆过某点”问题探究

☉江苏省溧水高级中学 徐茂炳

在反思中探究,在探究中反思：“以某线段为直径的圆过某点”问题探究

☉江苏省溧水高级中学 徐茂炳

原题重现：苏教版必修2第116页第27题

已知圆C：x2+y2－2x+4y－4=0，是否存在斜率为1的直线l，使以l被圆C截得的弦AB为直径的圆过原点？若存在，求出直线l的方程；若不存在，说明理由．

解法1：教参提供，设而不求，然后利用韦达定理．

设直线方程为y=x+b，将A（x1，y1）、B（x2，y2）代入C：x2+y2－2x+4y－4=0，可得x2+（x+b）2－2x+4（x+b）－4=0，整理得2x2+2（b+1）x+b2+4b－4=0．

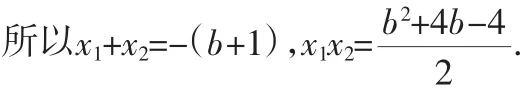
因为“以弦AB为直径的圆过原点”，所以x1x2+y1y2=0．

所以x1x2+（x1+b）（x2+b）=0，即b2+3b－4=0，所以b=－4或b=1．

反思1：在南师大编的《数学之友》上有这么一段话“直线与椭圆的复习着力于求出其有理根的问题（至于使用韦达定理的解法还是回避为好），特别是直线过椭圆的特殊点（顶点、焦点、中心），与椭圆的其他交点的坐标如何求出，应非常熟练”，那么对于直线与圆的问题就更应该回避韦达定理了，因为圆有很多椭圆没有的性质（比如垂径定理），在教学中往往因为解决某些问题时韦达定理比较好用或者教师的解题观念还没有转变过来，所以在教学中还是无法回避地讲解“设而不求”．因此老师一方面在应用“设而不求”解题，一方面《江苏省高考数学考试说明》又不要求学生掌握韦达定理．所以对学生来说一头雾水，不知道该用还是不该用．那么教师教学过程中应如何回避呢？

既然高考不要求掌握韦达定理或者说“设而不求”，那么教师教学中当然要少用，甚至不用，特别是

对中等学生．那么不用这个“老一套”，又该怎么求解呢？特别是对于这种“以某线段为直径的圆过某点”的问题．估计很少有教师去反思探究，或者有些老师觉得老办法不错也就不去多想了．可是到了考试的时候真正苦的还是学生．

探究1：首先考虑问题的背景是圆．我们初中学过“垂径定理”．高中课本课后有道习题又介绍了相交弦的求法．这些性质在很大程度上简化了圆中的很多计算．

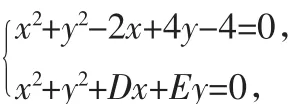
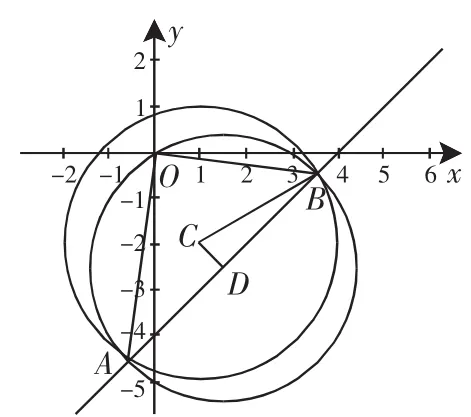
图1

反思2：解法2从过程上来看确实比“解法1”来得要慢，运算步骤多．所以很多老师即使知道这么写也不给学生讲，导致学生学习解析几何的时候非常困难．甚至很多学生考试的时候直接“跳过”．其实从这几年高考题来看，解析几何一般在第3到第5题之间区分度非常大，所以解析几何能够突破的话，对中等学生来说非常有帮助．

那么解法2应不应该跟学生讲呢？我觉得必须要讲．理由有三：一是这个解法和《考试说明》的要求一致，没有用到“超纲的韦达定理”，二是垂径定理是初中比较重要的一个性质，它的应用当然重要，也是知识的一个贯通过程，三是这个解法本身告诉我们关于圆的问题我们应该考虑圆的性质，这样可以大大简化运算．

探究2：解法2是从圆的方程入手的，那么我们能否直接从直线的方程切入呢？

解法3：直线CD的方程为y+2=－（x－1），即y=－x－1．

直线AB的方程可设为y=x+b．

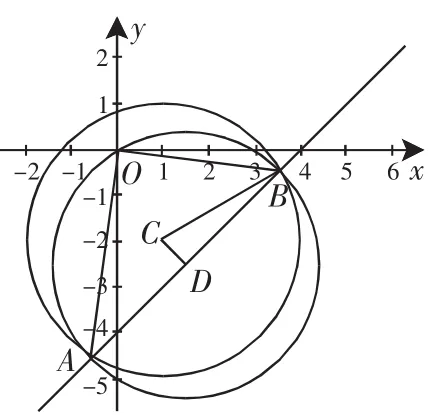
图2

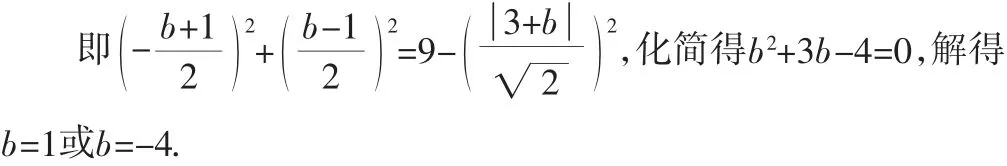
反思3：解法3和解法2有着异曲同工之妙.两种解法都回避了设而不求的方法.与《考试说明》高度一致.但是解法3比解法2更直接，而且运算更简便.但是都应用了圆的性质去简化运算和求解.

通过前面的反思和探究，我想说明的是：教师在教学的过程中，要紧扣《教学大纲》和《考试说明》，而不是经验主义，要以学生为教学主体，分析学生已知的和未知的，寻找适合学生理解和掌握的方法.虽然解法2和解法3相对于解法1要浪费时间，感觉“吃亏”，但是学生容易接受和理解.

刚才以课本题为例说明了“设而不求”的方法确实可以在新课程标准中把它删去.那么江苏的高考题中是怎么体现的呢？也就是说教学中不介绍“设而不求”在平时模拟考试中会不会吃亏呢？我想不但不会吃亏，有时候反而有优势.至少江苏高考是这样的.

（1）求椭圆的方程.

（3）是否存在实数k，使直线y=kx+1交椭圆于P、Q两点，以PQ为直径的圆过点D（－1，0）？若存在，求出k的值；若不存在，请说明理由.

图3

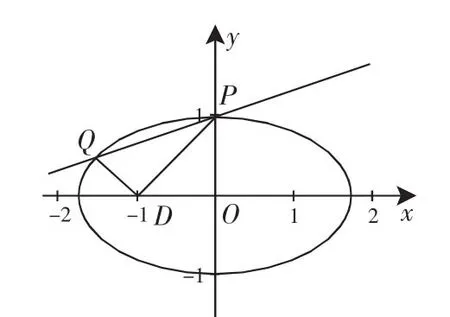
图4

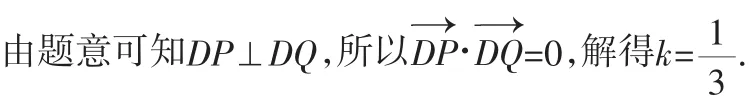
反思4：这道题是2012届江苏一模一道联考题，这道题考查的是直线与椭圆.如果用韦达定理“设而不求”，那解出这道题需要绕很多弯子.反之，如果利用方程的思想“设而求之”，反而比较容易突破.其实江苏近几年高考题都是这个套路.大家可以参考文［1］中的《透过现象看本质》一文.

教师的教是为了学生的学.所以教师在教学过程中应该研究学生的学情和《新课程标准》，不能一味儿的经验主义和拿来主义.其实现在很多我们认为学生知道的已经在初中教材中删掉了，比如十字相乘法和韦达定理.因此我们在教学过程中应该抓住学生，离开了学生的“教学”是低效的甚至是无效的.有时候我们经常责怪学生怎么老是不懂或者老是犯错，其实教师如果多反思自己的教学的话，往往更能解决问题.在教学中反思，在反思中教学，做一个有思想的教师，才能教出会思考的学生.

1.徐茂炳.透过现象看本质［J］.中学数学（上半月·高中），2012（8）.