轴对称在初中数学中的灵活运用

☉江苏省常州市新北区实验中学 俞 艳

轴对称在初中数学中的灵活运用

☉江苏省常州市新北区实验中学 俞 艳

轴对称是初中数学教学中的核心知识点，经常显身于历年的各地中考中，教学中学生容易理解，但难以在具体的数学问题中灵活运用，也就成了学生容易失分之处.如何灵活利用轴对称来解决有关数学问题呢？下面通过例题就这话题谈谈体会.

一、巧借轴对称求生活中的最短距离

两点之间线段最短，这是大家都知道的一个事实.在一些实际问题中，我们会遇到求不在一条直线上的两条或三条线段和的最小值问题，要解决这类问题，可借助轴对称的相关知识，求出距离最短的问题.

例1 如图1，公路m一旁有两蔬菜生产基地A、B，现要在公路上建一货物中转站.

（1）若要中转站到A、B两蔬菜生产基地的距离相等，中转站应建在何处？

（2）若要使中转站到A、B两基地的距离之和最短，应建在何处？

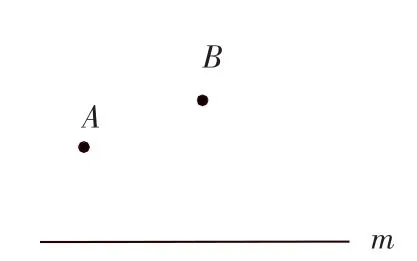
图1

分析：（1）由“线段垂直平分线上的点到这条线段两端点的距离相等”可知蔬菜基地应建在AB的垂直平分线上，又因为货物中转站要建在公路上，所以AB的垂直平分线与公路m的交点就是中转站应建的地点.（2）如果A、B两点在直线m的两侧，连接AB与m的交点即为所求，由于现在A、B两点在m的同侧，因此可考虑作A点关于m的对称点C，由轴对称的性质，可知直线m上任意一点到A、C的距离相等，这样就把直线m上一点到点A的距离转化为到点C的距离，因此连接CB与m的交点即为所求.

解：（1）作AB的垂直平分线交m于点P，点P就是所要求的蔬菜基地的位置.

（2）作点A关于m的对称点C，连接BC交m于点D，点D就是所要求的蔬菜基地的位置.

例2 如图2，已知养牛营地在点M处，每天放牛人要赶着牛群到河边饮水.

（1）请作出从营地到河边饮水的最短路线.

（2）如果饮完水后，再到

草地吃草，然后再次回到营地，请作出最短的放牛路线图.

分析：这是一道生活中的问题，根据题意抽象出数学问题是解题的关键.（1）可抽象出点到直线的最短距离.（2）可抽象出这样的数学模型：直线a、b间有一点M，试分别在a、b上求出一点M，使M点与这两点构成的三角形的周长之和最小，要求周长之和最小，即要求三条线段的和最小，根据题目意思，可利用轴对称的有关性质转化为两点之间线段最短的问题.

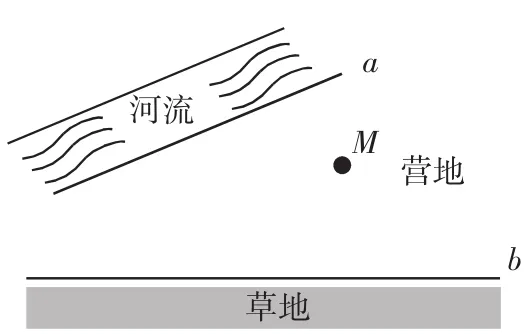
图2

解：（1）过点M作MP⊥a于A，MP即为最短路线.

（2）分别作点M关于a、b的对称点A、B，连接AB分别交a、b于点C、D，则最短的放牛路线为：M→C→D→M.

例3 甲、乙两个单位分别位于一条河的两旁，河的两岸分别为L1、L2，现为了方便两单位的通行方便，准备合作修建一座桥.（桥必须与河道垂直）.

（1）桥建在何处能使甲、乙到桥的距离相等？

（2）桥建在何处能使甲到乙的路线最短？

解析：（1）作点B关于河道的对称点B1，连接AB1，作AB1的垂直平分线，与街道靠近A的一侧相交于A1，过A1建桥即符合要求.

（2）将点A沿竖直向下的方向平移至点A2，使AA2的长等于河道的宽度，即桥宽，连接A2B与河道靠近B的一侧交于点B2，过B2点建桥即符合要求.

二、灵活运用轴对称的性质求角度、角与角之间的关系、边与边之间的关系.

图3

例4 如图3，把一张矩形纸片ABCD（AD∥BC）沿EF折叠后，点C、D分别落在C′、D′的位置上，EC′交AD于点G．已知∠EFG=58°，那么∠BEG=_________．

分析：根据折纸的操作原理可知C点与C′点关于EF对称，即EC和EC′关于EF对称，所以∠CEF＝∠GEF，再根据∠EFG和∠CEF的关系即可求得.

解：根据折叠原理，可知EC和EC′关于EF对称.所以∠CEF＝∠GEF.

由AD∥BC，得∠EFG＝∠CEF.

所以∠BEG＝180°－2×∠EFG＝180°－2×58°＝64°.

例5 如图4，把△ABC纸片沿DE折叠，当点A落在四边形BCDE内部时，∠A与∠1+∠2之间有一种数量关系始终保持不变，请试着找一找这个规律，你发现的规律是（ ）.

A.∠A=∠1+∠2 B.2∠A=∠1+∠2

C.3∠A=2∠1+∠2 D.3∠A=2（∠1+∠2）

分析：折叠前后的部分关于折痕所在直线对称，分别延长BE、CD相交于点A′，则点A′就是点A的对称点．连接AA′，根据轴对称的性质，可知直线DE是线段AA′的垂直平分线，所以EA=EA′，DA=DA′.所以∠EAA′=∠EA′A，∠DAA′=∠DA′A.

又因为∠1= ∠EAA′+∠EA′A=2∠EAA′，∠2= ∠DAA′+∠DA′A=2∠DAA′，所以∠1+∠2=2∠EAA′+2∠DAA′=2（∠EAA′+∠DAA′）=2∠DAE.

因此，应该选B.

当然，轴对称的运用是多维度的，只要在数学教学中把握好思维解决的支点，就能化难为易，运用自如.

图4