隐性目标函数的破解策略例析
☉河北省邱县第一中学 杜 建
在高考数学命题“以能力立意”的趋势下,线性规划问题也由单纯的知识型考查向知识和能力立意并举的考查形式转变,尤其是目标函数与其他知识交汇后,呈现出多样性和隐蔽性的特点,对学生综合运用知识分析问题和解决问题的能力提出了更高的要求.本文根据近几年出现的精彩问题,阐释破解隐性目标函数的几种策略.
一、利用其他知识,寻求目标函数

图1
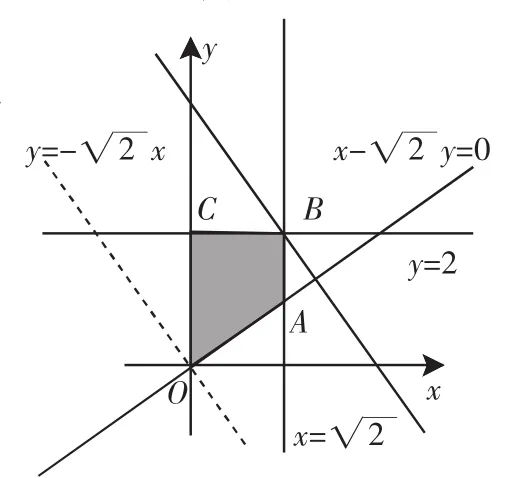
图2
例1(2011年湖北理)已知向量a=(x+z,3),向量b=(2,y-z),且a⊥b.若x、y满足不等式|x|+|y|≤1,则z的取值范围为___________.
解:由题意得不等式|x|+|y|≤1约束下的可行域如图1所示(含边界).因为a⊥b,所以(x+z,3)·(2,y-z)=0,即z=2x+3y.由“顶点坐标代入法”,得直线z=2x+3y过点(0,-1)时,z=2x+3y取得最小值-3,直线z=2x+3y过点(0,1)时,z=2x+3y取得最大值3.因此z的取值范围为[-3,3].
例2 (2011年广东理)在平面直角坐标系xOy上的区域D由不等式组给定.若M(x,y)为D上的动点,点A的坐标为的最大值为____________.
解:由题意得在平面直角坐标系内不等式组所确定的可行域如图2阴影部分所示.


点评:上述两个例题将目标函数向量化.通过向量的数量积运算寻求目标函数,从而使目标函数的几何意义“截距化”,利用“顶点坐标代入法”求出目标函数的最值或取值范围.虽然题目看似简单,但命题人巧妙地把向量知识与线性规划问题结合起来,不失为一道考查学生综合运用知识分析问题和解决问题能力的好题.
二、利用距离公式,改造目标函数

图3
例3 (2011年江西理)对于实数x、y,若|x-1|≤1,|y-2|≤1,则|x-2y+1|的最大值为____________.
解:由题意得点(x,y)在约束条件下的可行域为正方形ABCD(含边界),如图3阴影部分所示.由于可以看成可行域内的点(x,y)到直线x-2y+1=0的距离的倍,因此,当x=0、y=3时,|z|=|x-2y+1|取得最大值5.
三、利用斜率公式,明确目标函数
解:由题意得点D由不等式组所确定的可行域如图4阴影部分所示.令,根据几何意义,t的值即为可行域内的点与坐标原点连线的斜率,显然t的取值范围为

图4
点评:本例看似毫无头绪,令人无从下手.但经过巧妙“变形换元”,目标函数的几何意义“跃然纸上”,然后“分离常数”,构造关于t的函数,利用函数的单调性得出目标函数的取值范围.

解:由题意得不等式组所确定的可行域如图5阴影部分所示.cos∠POQ的值越小,∠POQ的张角越大.显然,由图形可知:∠AOB即是所求角.


点评:本例中的目标为求角的余弦值,几何意义看似无迹可寻.但根据斜率公式k=tanα,把角与斜率联系起来,所求目标函数的最值“迎刃而解”.
四、利用二次函数,变形目标函数

例6(2008年上海文第11题改编)在平面直角坐标系中,A、B、C点的坐标分别为(0,1)、(4,2)、(2,6).如果P(x,y)是三角形围成的区域(含边界)上的点,则w=xy的最大值是____________.
解: 由题意得A、B、C三点所确定的可行域如图6所示.要求w=xy的最大值,实质上是求图6阴影部分所示的矩形面积.易知在同一水平线上,点P越靠右,矩形面积越大;在同一竖直直线上,点越P靠上,矩形面积越大.因此只有当点P在线段BC上时,才能使矩形面积最大,显然,线段BC的方程为y=-2x+10(2≤x≤4).所以w=xy=x(-2x+10)=-2x2+10x,故当
点评:本例中目标函数的几何意义很明确:求矩形面积的最大值.难在判断何时点P才能使矩形有最大面积,通过分析只能在可行域的边界上,这样求出所在边界的直线方程,通过换元变形将问题转化成闭区间上二次函数的最值问题,从而使问题得到解决.

