柯西不等式在解析几何中的应用
☉湖北省襄阳市第一中学 黄 涛 王 勇(特级教师)
柯西不等式具有对称和谐的结构,应用的关键在于抓住问题的结构特征,找准解题的正确方向,合理地变形、巧妙地构造.作为新课程的选修内容,柯西不等式(简记为“方和积不小于积和方”)在数学的多个领域都有着广泛的应用,不仅在代数方面能够帮助我们解决问题,而且在解决解析几何问题时也给我们带来极大的方便.下面分类例析,旨在探索题型规律,揭示解题方法.
一、研究最值问题

图1
例1 如图1所示,在平面直角坐标系xOy中,等腰直角三角形AOB的一直角边为1,在此三角形内任取点P,过P分别引三边的平行线,与各边围成以P为顶点的三个三角形(图中阴影部分),求这三个三角形的面积和的最小值以及达到最小值时P点的位置.
分析:此题需要设出P点坐标,并用其表示出三个三角形的面积之和,再利用柯西不等式求最值.
解析:由题意可知,AB所在直线的方程为x+y=1,设P点坐标为P(xP,yP),则以P为公共顶点的三个三角形的面积和为


评注:解此题的关键是用P点的坐标表示出三个三角形的面积.观察图形,可以看出:靠近x轴的等腰直角三角形的直角边长为yP,靠近y轴的等腰直角三角形的直角边长为xP,靠近斜边的等腰直角三角形的直角边长为1-xP-yP.
例2 试用柯西不等式推导平面上点到直线的距离公式.
解析:已知点P1(x0,y0)及直线l:Ax+By+C=0(A2+B2≠0).设点P2(x1,y1) 是直线l上的任意一点,则Ax1+By1+C=0,①|P1P2|=
P1、P2两点间距离|P1P2|的最小值就是点P1到直线l的距离,下面求|P1P2|的最小值.
根据柯西不等式,得:

将①、②代入上式,得:

当且仅当A(y0-y1)=B(x0-x1),即P1P2⊥l时,③式取等号.
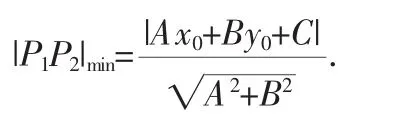
故点P1(x0,y0)到直线l:Ax+By+C=0的距离公式为
评注:本题通过利用柯西不等式求两点间距离的最小值而推导出点到直线的距离公式,思维简约,过程简捷.
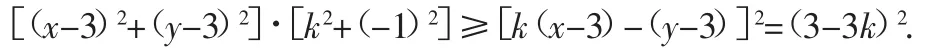
因为(x-3)2+(y-3)2=6,所以6(k2+1)≥(3-3k)2,即k2-6k+1≤0,解得
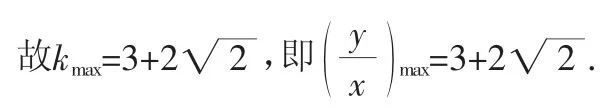
评注:本题解法很多,其中利用柯西不等式求解如同神来之笔,值得细细品味和充分借鉴.

例4 设椭圆中心在坐标原点,A(2,0),B(0,1)是它的两个顶点,直线y=kx(k>0)与AB相交于点D,与椭圆相交于E、F两点.求四边形AEBF面积的最大值.
设点F(x,y)(x>0),所以四边形AEBF的面积S=2(S△OBF+S△OAF)=x+2y.
评注:本题用到柯西不等式的变形公式:设a1、a2、…、an为实数,b1、b2、…、bn为正数,则当且时取等号.此举大大降低了问题的难度,达到了化难为易、化繁为简、化陌生为熟悉的目的.
二、界定范围问题

由柯西不等式,得:

评注:本题利用柯西不等式,结合cos2α+sin2α=1这一条件,轻车熟路的几步代数推理,就使问题迎刃而解了.
解析:易知椭圆与x轴、y轴的正半轴的交点分别为M(a+1,0)、N(0,a-1).

故|MN|可以小于2a.
评注:本题通过利用柯西不等式界定|MN|的取值范围而解决问题,收到了化难为易、化繁为简、一招制胜之奇效.
例7 求使直线xcosθ+ysinθ=2和椭圆x2+3y2=6有公共点的θ的取值范围(0≤θ≤π).
分析:此题为直线与圆锥曲线的位置关系问题,通常的解法是建立方程组,消元,利用判别式来解,这种方法运算量较大,下面我们通过构造柯西不等式求解.
解析:由柯西不等式,得:


评注:由于直线方程是关于x,y的一次式,而椭圆的方程是关于x,y的二次式,这为构造柯西不等式提供了可能.变形时要调整系数以满足曲线方程中的形式.
三、破解相切问题
分析:利用柯西不等式解决直线和圆锥曲线的位置关系问题,可以减小计算量,增强直观性,是十分有效的好方法.
解析:设直线方程为Ax+By+C=0,由经过点P(5,1)得C=-(5A+B).
于是直线方程可表示为A(x-2)+B(y+3)=3A+4B.
由柯西不等式,得:

直线与椭圆相切时不等式取等号,即(3A+4B)2=9A2+4B2,解得B=0或B=-2A,所以要求的切线方程为x-5=0或x-2y-3=0.
评注:拆、凑、配是应用柯西不等式解题的过程中对式子变形的主要手段,敬请同学们通过本例去体会方法,领悟技巧.
例9 已知直线y=(1-x)tanθ与双曲线-x2+y2cos2θ=1相切求切线方程和切点坐标.
分析:本题直接应用直线与圆锥曲线的位置关系求解比较繁杂,而应用柯西不等式比较直观,简单明了.
解析:由柯西不等式,得:

所以切线方程为y=x-1或y=1-x,切点坐标为(-1,±2).
评注:直线与圆锥曲线的相切问题一直是解析几何中的重点和难点,用判别式法求解运算量大,易出错.而柯西不等式为我们解决这类问题提供了简洁而有力的方法.

