危险品泄漏事故后人群动态疏散路径优化

陈钢铁，帅 斌

(西南交通大学交通运输与物流学院，四川成都610031)

人群的应急疏散是当危险品在人群发生灾害时，将危害区的人群在最短的时间内疏散到安全区内。人的应急疏散是应急减灾系统中的一个重要组成部分，国内外很多学者展开了相关的研究。三隅二不二，等［1］及杉万俊夫［2］揭示了群体中的领导者和引导人对其他人员的影响以及缩短疏散时间的效果;张玉春，等［3］对人员疏散随机性的公路隧道火灾风险分析，对隧道风险进行了仿真;王兆其，等［4］利用虚拟现实技术，在计算机生成空间中建立公共设施和人群的三维模型，设定各种可能发生的安全危机和相应的疏散预案，模拟并三维地展示人群疏散场景;吴娇蓉，等［5］借助空间句法对单线和3线轨道车站的空间进行研究，综合考虑空间形态分析变量便捷度指标、站内人流动线的特征、流线冲突点、行人感知等因素，界定轨道站火灾情况下的安全区域，指出轨道站站台发生火灾等事故时疏散过程应分为两个阶段，每个阶段应分别规定疏散时间要求;袁媛，等［6］在提出的应急疏散路径选择模型中，将通过疏散路径所需的总疏散时间最短作为优化目标，将各弧段上的通行速度表示为关于时间的连续递减函数，并对不同弧段的速度函数设置了不同的衰减参数。笔者利用动力学原理描述危险品发生泄漏后人员在应急疏散过程中的速度，动态地分配人群，建立以总疏散时间为最短的模型，分析人的疏散，最后得出最优的疏散方案。

1 问题描述与模型建立

危险品发生泄漏后，首先考虑到危害区人群的疏散问题。在人群应急疏散过程中，最短的时间把人群疏散到安全区域是首先考虑的目标。应急疏散路网中，应急疏散中的人群可以选择多条路径，所有疏散路网中疏散路径上人的密度是时变的。随着人群密度的增加，疏散人群的速度不断减小。所以应急疏散路网上通过各路径的时间不是确定，而是时变。笔者重点研究在危险品泄漏后，人群密度和速度的关系，建立人群疏散速度和人群疏散密度关系后，再进行路径优化。

1.1 人群流动的动力学速度模型

利用基本动力学的原理对应急疏散中的人群移动进行描述。在紧急情况下人群中的每一个人基本上受到前后人群、两侧紧急疏散人群及个人驱动等3个因素的影响。前后人群、两侧紧急疏散人群因素为应急疏散中本人必须改变自身的速度以适应周围应急疏散人群的影响，个人驱动因素为疏散本人想超越人群，尽快摆脱危险的自身的驱动力。

根据上面的分析并参考文献［7-8］，假设危险品泄漏后疏散中人群的疏散速度受到3个因素的影响。

1.1.1 应急疏散人群中前后人流因素对个人疏散速度的影响

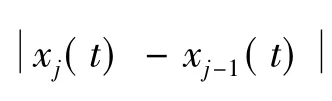
1.1.2 应急疏散人群中侧面人流因素对个人的影响作用fj

在应急疏散过程中，同路段上人群中的个人为了避免受到旁人挤压或拥挤，应急疏散人群中的第j个人还会受到一个侧面“抑制力”fj的作用。这个侧面抑制力假设是大于0的，随着越来越接近旁边人，该力变得越来越大。

1.1.3 个人驱动力的影响作用Pj

个人驱动力代表了人们想要摆脱周围人群，超越前面人群的一种自我驱动力Pj。个人驱动力与人的年龄、性别、心理和生理等有着很大的关系，它是一个向前的驱动力。如果第j个人的质量为Mj，根据牛顿运动定理，第j个人的影响合力为:

根据公式(1)推导得出:

式中:ρ1m和ρ2m分别为在紧急疏散人群中个人前进方向的最大线密度和两侧方向的最大线密度，人/m，表示人员在此密度下的拥挤或挤压下，人群中的个人不能移动前进;ρ1c和ρ2c为人群中的个人前进方向和两侧方向自由移动的临界密度，人/m;ρ为面密度，即在紧急疏散的单位面积中人群的数量，人/m2;vm为自由移动时最大速度，m/s，通常表示没有拥挤情况下的人群平均移动速度。

公式(2)右边的3个部分分别代表:①应急疏散人群中个人前后方向的拥挤或挤压作用，疏散速度和密度基本是对应的对数关系，疏散过程中的人群密度越大，人群疏散的密度越小;②疏散人群中的个人两侧方向的作用因素，疏散人群的速度和疏散人群的密度基本呈线性关系，疏散人群越拥挤则疏散人群的速度就越慢;③疏散人群中个人的自身驱动力(α，β，γ分别为这3个因素的权重，表示这3个因素对人员前进方向速度的影响程度，其取值主要依靠观测或实验数据取得)。

1.2 假设条件

1)设危险品泄漏后人群应急疏散网络G(V，A)，其中 V={v1，v2，…，vn}为有限节点集合，A 为有限弧集合，A⊆V ×V。v1，v2，…，vn为危险品泄漏后人群应急疏散网络中的节点集合，v1为危险品泄漏后人群应急疏散网路的初始位置，即危害区的初始点。vn为危害区人群疏散到安全区域的最终点。

2)lij为应急疏散路网中节点vi，vj之间应急路网中路段的长度，(vi，vj)∈A。

3)vij为应急疏散路网中节点vi，vj之间应急路网中路段上应急人群的速度，(vi，vj)∈A，如式(2)。

4)tij表示疏散人群在应急路段(vi，vj)上所需要的时间;ti为应急疏散人群到达应急疏散路段(vi，vj)上的节点vi时刻，tj为应急疏散人群到达应急疏散路段(vi，vj)上的节点 vj时刻，则:tij=tj-ti。

1.3 模型建立

利用动态动力学原理对疏散人群在路网上的速度进行描述，以人群疏散时间最小为目标建立危险品泄漏后动态人群疏散模型。

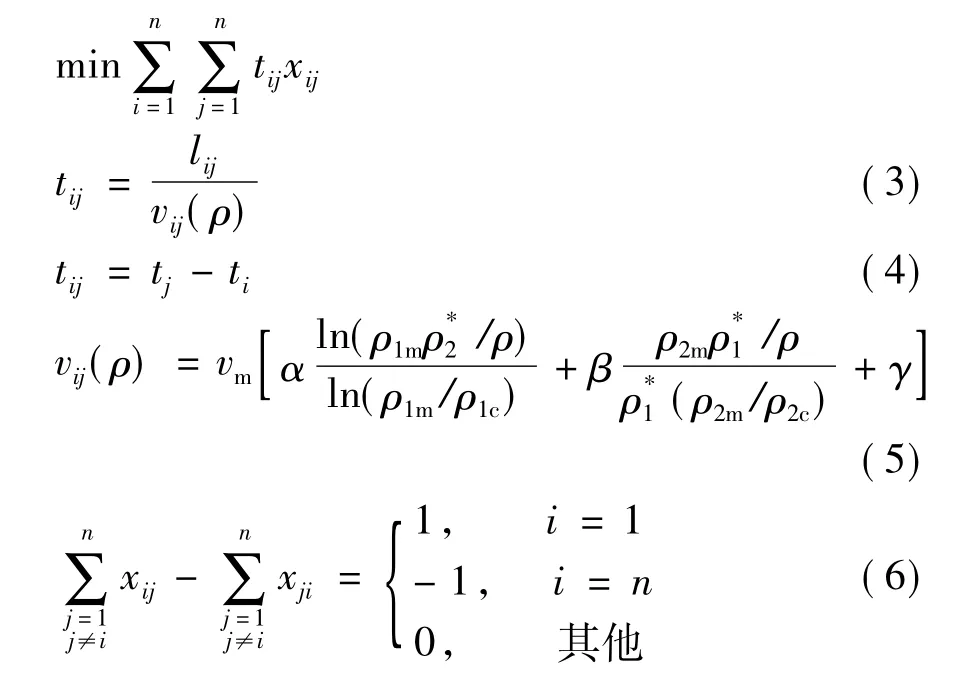
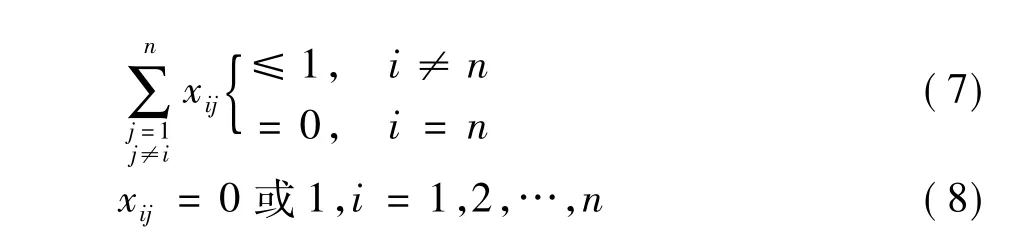
式(3)、式(4)为扩散性危险品泄漏后人群紧急疏散时间的递推关系，应急疏散人群在时间tij内以时变速度vij(ρ)经过应急路径(vi，vj);式(5)表示危险品泄漏后人群在各个路径上应急疏散的速度;约束(6)表示xij的取值构成危害区域v1到应急疏散安全区域点vn的最少有一条可行的应急疏散路径;约束(7)为危险品事故泄漏后疏散路网疏中不含回路;约束(8)为决策变量xij的类型约束。

2 模型的求解算法

量子粒子群优化(Quantum Particle Swarm Optimization，QPSO)直接采用量子位的概率幅对粒子的位置进行编码，用量子旋转门更新量子位的概率幅，由此完成粒子位置的更新。

式中:xi为应急疏散车辆搜索粒子位置;K为当前迭代次数;pij为第i个粒子第j个分量的最优值;β为收缩扩张系数;αj为种群第j个分量的中心位置;m为寻找最优解的粒子数;n为粒子的维数;u为0～1之间的随机生成数。

QPSO在寻找最优解得过程中，容易过早收敛。因此可以采用混沌的遍历性和随机性的特点，对量子粒子群算法进行修改。

对 max f(x1，x2，…，xi，…，xn)，ai≤ xi≤ bi，问题进行优化计算，计算过程如下:

步骤1:混沌过程产生初始向量。随机产生一个n 维向量 z1=(z11，z12，…，z1j，…，z1n)，0≤z1j≤1;根据混沌原理及方法计算 z2，z3，…，zi，…，zM;将 zi的各个分量分配到相应优化变量中，则xij=aj+(bj-aj)zij。

步骤2:计算每个粒子的目标函数值f，从M个初始应急疏散车辆搜索粒子中选择性能较好的m个应急疏散车辆搜索粒子作为目标函数的初始解。假设现在m个较好性能的粒子的位置和目标值作为各自的最优值pbest，并m性能较好的粒子中选择位置和目标值选择最优值gbest。

步骤3:根据式(1)更新m个粒子位置，并计算更新后各粒子目标值。

步骤4:混沌扰动。混沌扰动波动的范围λ设定为粒子位置取值范围的r倍(r的取值随迭代次数的增加而减小)，则Δx=-λ+2λu产生扰动向量Δx=(Δx1，Δx2，…，Δxi，…，Δxn)，令 xi=xi+ Δxi，并计算目标值为f'，如果f'＜f，则令f'=f，对相应的粒子群位置进行更换。

步骤5:更新所有粒子群的目标值pbest，并从所有性能较好的粒子群中选取gbest。如达到条件则终止，否则继续从步骤3进行循环。

3 算例

某地区危险品在运输过程中发生灾害(图1)，S点为事故发生地，A、B、C、D为安全地点，在S点处有1 000个人需要疏散。从S点到安全地点有4条路径，其中SA=360 m，SB=370 m，SC=420 m，SD=350 m，每条路径宽度为2 m。

图1 疏散路径Fig.1 Crowd emergency evacuation road network

［7，9］选择参数，ρ1m=3 人/m，ρ2m=2人/m，ρ1c=0.89 人/m，ρ2c=1.33 人/m，vm=2m/s。α =0.42，β =0.131，γ =0.27。在拥挤状态下疏散人数自由组合，计算S点处有1 000个人需要疏散最短疏散时间的最优疏散方案。

在WIN7操作系统，内存:4G，CPU:Inter P7450的环境下，通过MATLAB编程，计算机上运行时间为91.042 0 s，最后计算出最短的疏散时间为288.756 2 s。最优的应急疏散方案为在SA路径上疏散人数为370人，SB上疏散人数为127人，在SC上疏散人数为115人，SD上疏散人数为388人。模拟退火算法的迭代过程如图2。

图2 量子粒子群优化的迭代过程Fig.2 Iterative process of simulated annealing map

4 结语

利用动力学原理对人的疏散时的速度进行模拟，建立了以总疏散时间最短的模型。人群中的数量在疏散过程中随机组合，利用量子粒子群优化对模型进行求解。对总的疏散时间和路径进行优化。保证了人群以最短的时间进行疏散，最后通过算例验证了模型和算法的有效性。考虑人的行为，复杂网络的疏散以及快速算法是进一步研究的方向。

参考文献(References):

［1］ 三隅二不二，佐古秀一.在模拟紧急受灾情况下的领导者的指挥行为对集合成员追从行为的影响效果研究［J］.试验社会心理学研究，1982，17(22):49-59.

Fuji Misumi，Sako Shuichi.Disaster situations in a simulated emergency command leader chasing behavior on the set of members of the research results from the behavior［J］.Experimental Social Psychology，1982，17(22):49-59.

［2］ 杉万俊夫.紧急避难状况时新的避难引导方法的开发［J］.社会心理学年报，1983，24:47-64.

Shan Wan Toshio.State of emergency shelter when the new method to guide the development of evacuation ［J］.Annual Report of Social Psychology，1983，24:47-64.

［3］ 张玉春，何川.基于人员疏散随机性的公路隧道火灾风险分析［J］.土木工程学报，2010，11(7):38-43.

Zhang Yuchun，He Chuan.Randomness in the evacuation road tunnel fire risk analysis［J］.Civil Engineering Journal，2010，11(7):38-43.

［4］ 王兆其，毛天露，蒋浩，等.人群疏散虚拟现实模拟系统——Guarder［J］.计算机研究与发展，2010，47(6):77-82.

Wang Zhaoqi，Mao Tianlu，Jiang Hao，et al.Virtual drilling system for crowd evacuation under emergency scheme［J］.Computer Research and Development，2010，47(6):77-82.

［5］ 吴娇蓉，胡山川，冯建栋.轨道站火灾疏散安全区域界定研究［J］.同济大学学报:自然科学版，2010，38(3):36-41.

Wu Jiaorong，Hu Shanchuan，Feng Jiandong.Evacuation of virtual reality simulation system-guarder［J］.Journal of Tongji University:Natural Science，2010，38(3):36-41.

［6］ 袁媛，汪定伟.灾害扩散实时影响下的应急疏散路径选择模型［J］.系统仿真学报，2008，20(6):1563-1566.

Yuan Yuan，Wang Dingwei.Diffusion under the influence of realtime disaster emergency evacuation route choice model［J］.Journal of System Simulation，2008，20(6):1563-1566.

［7］ 袁建平，方正，卢兆明，等.车站客流观测及其对人群疏散动力学模型的验证［J］.西安建筑科技大学学报，2008，40(1):108-113.

Yuan Jianping，Fang Zheng，Lu Zhaoming，et al.Station observations and its impact on passenger evacuation dynamics model validation ［J］.Xi’an University of Architecture and Technology，2008，40(1):108-113.

［8］ Fang Z，Lo S M，Lu J A.On the relationship between crowd density and movement velocity［J］.Fire Safety Journal，2003，38(4):271-283.

［9］ 崔喜红，李强，李学东，等.公共场所疏散引导人静态布局优化算法及其应用［J］.系统仿真学报，2008，20(22):6285-6288.

Cui Xihong，Li Qiang，Li Xuedong，et al.Public places to guide people to evacuate the static layout optimization algorithm and its application［J］.Journal of System Simulation，2008，20(22):6285-6288.