传感器部分失效的网络控制系统H∞容错控制
彭高丰, 马振中, 夏明霞, 刘红平
(长沙师范高等专科学校,长沙 410100)
0 引言
网络控制系统是面向复杂分布式控制应用或控制对象,采用计算机和网络通讯技术,在传感器、执行器件和控制器等智能节点或子系统间传递控制和管理信息,完成复杂的整体控制功能,从而形成的数字通信网络。网络控制系统摆脱了传统点对点连接的束缚,打破了系统在空间位置上的限制,拓宽了控制活动的场所,降低了系统连接的复杂性、运行成本和维护费用,应用范围越来越广泛。网络控制系统已经引起了学术界的广泛关注[1-10]。
随着网络控制系统的日益复杂,无法避免网络传输中的时延、丢包以及网络调度等问题,同时系统中的传感器等节点发生失效故障,也会导致系统失去所期望的动静态特性乃至失稳,因而研究传感器出现故障的时延网络控制系统的鲁棒容错控制具有较强的现实背景。
目前网络控制系统的鲁棒容错控制研究中所采用的传感器故障模型都为开关矩阵这种极端模型(正常为 1,失效为 0)[1-2,6-7,10],而在实际网络控制系统中的故障更多的是部分失效情形。
本文研究了有界控制输入下闭环网络控制系统的H∞容错控制问题。针对网络控制系统存在传感器等节点部分失效和外部扰动的情况,研究了系统渐近稳定性问题,给出了系统渐近稳定的条件,并研究了闭环系统渐近稳定下H∞控制器存在的充分条件及设计方法。
1 问题的描述
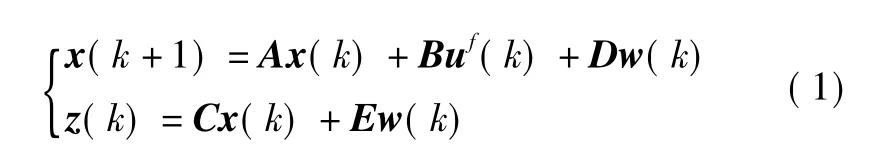

式中:x(k)∈Rn,uf(k)∈Rm,w(k)∈Rl,z(k)∈Rq分别为系统状态、控制输入、有限能量的外部干扰和量测输出;A,B,C,D,E是具有相应维数的常数矩阵。传感器失效控制输入表示为

式中,R为传感器失效的系数矩阵,且R=diag[r1,r2,…,rm]。其中:ri',为所给定的常数,第 i个传感器完全失效时ri=0,完全正常则ri=1。
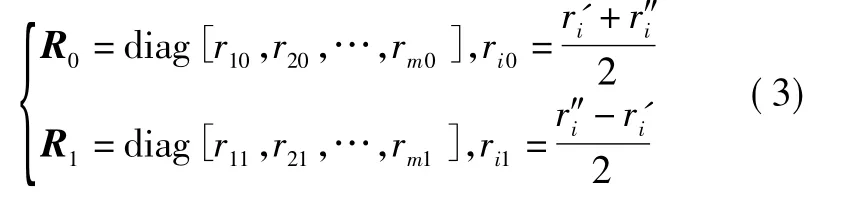
因此矩阵R可表示为

具有外部扰动和时延的网络控制系统如图1所示。

图1 网络控制系统结构Fig.1 Construction of networked control system
假设网络造成的前向通道(传感器到控制器)时延为 τ1,反馈通道(控制器到执行器)时延为 τ2,τ1和τ2均为正整数。对于网络控制系统(1),如果不考虑数据包的丢失,则在k时刻系统控制器得到的反馈信息为系统对象在k-τ1时刻的状态;控制器根据得到的信息计算控制量,并通过网络传输到执行器,执行器获得这个控制量的时刻为k+τ2,并在该时刻将控制量作用到控制对象。因此,从传感器到执行器,整个网络的时延为 τ1+ τ2,即系统(1)可写成

将系统状态和系统输入组成增广状态,则可转换为

H∞容错控制就是把H∞控制方法运用到网络化控制系统的容错控制,采用固定的控制器来确保闭环系统对特定的故障和外部干扰不敏感,并能使系统保持稳定和具有适当的性能指标。这种控制方法属于网络控制系统中的被动控制。
2 主要结果
定理1对于网络控制系统(6),假设外部扰动w(k)=0,并存在正定矩阵P和正定矩阵Q,满足如下条件
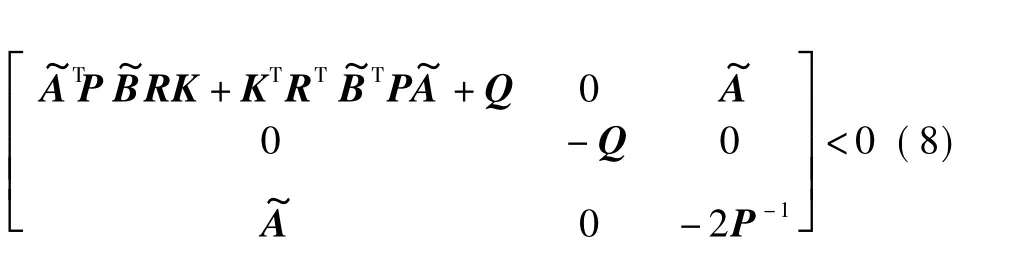
则系统渐近稳定。
证明:考虑系统(6),构造Lyapunov函数V(k)=由于 P,Q 都是正定矩阵,可知ΔV(k)是正定矩阵。假设w(k)=0,,则 ΔV(k)的前向差分
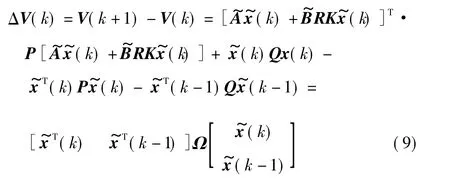
因此,由Schur补定理知Ω<0与不等式(8)等价,定理1得证。
定理2考虑具有控制约束和时延为τ1+τ2的网络化控制系统(6),给定常数γ>0,ε>0,如果存在正定对称矩阵P和正定矩阵Q,使得以下矩阵不等式成立。

则具有容错控制器u(k)=Kx(k)的闭环系统(6)是渐近稳定的,且具有H∞性能指标γ。
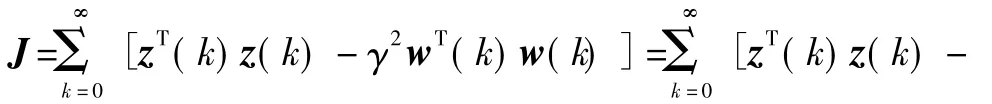




3 仿真结果分析
考虑网络控制系统(6)具有如下参数
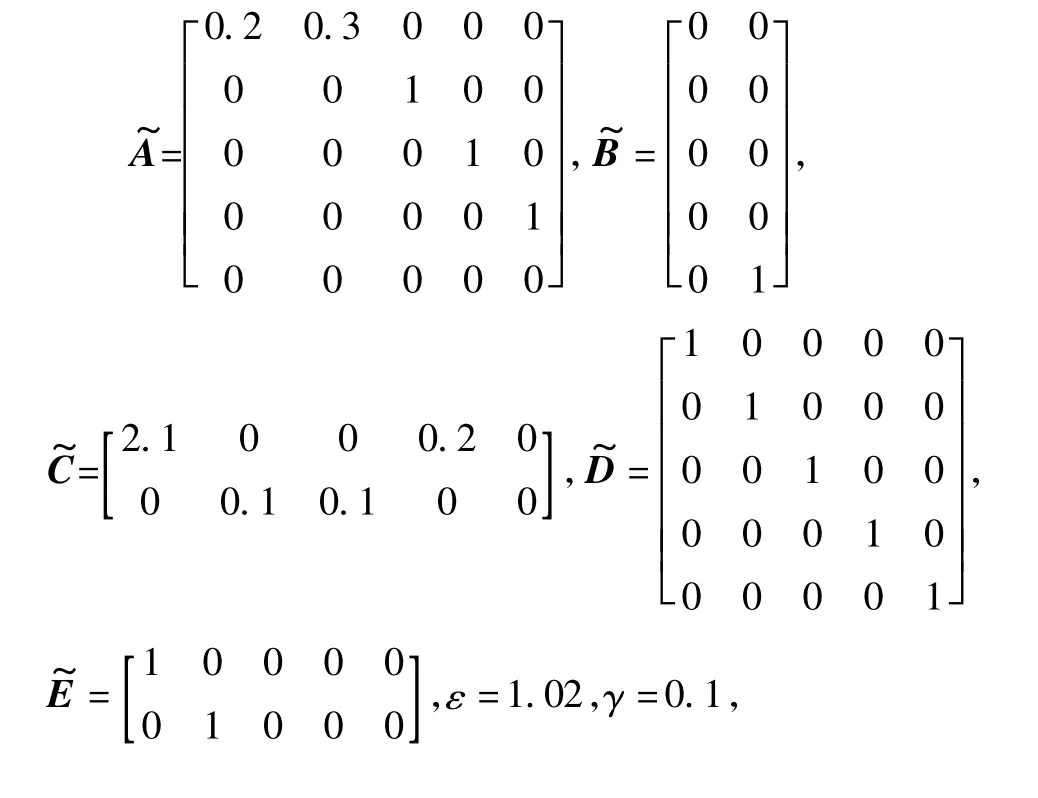


把以上参数代入不等式(10),利用Matlab toolbox LMI可以验证线性矩阵不等式成立,因此网络控制系统(6)是渐近稳定的。
从图2可以看出,系统的5个零输入状态 x1,x2,x3,x4,x5在有外部干扰的情况下呈递减趋势,经过一定时间都能趋近零,说明系统是渐近稳定的。由此证明了本文所给结论的正确性。
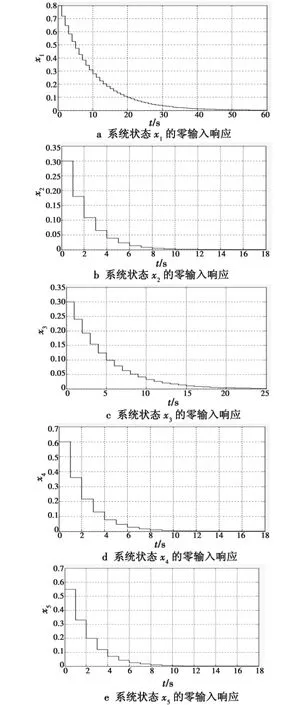
图2 系统状态的零输入响应Fig.2 Zero-input response of system status
4 结束语
本文研究了一类存在传感器部分失效、固定时延和外部扰动的网络控制系统H∞容错问题,给出了系统渐近稳定下H∞控制器存在的条件及设计方法。仿真结果分析说明了方法的有效性。
[1] GUO Yinan,ZHANG Qinying.Fault-tolerant guaranteed cost control of uncertain networked control systems with timevarying delay[J].International Journal of Computer Science and Network Security,2009,9(6):113-118.
[2] 霍志红,方华京.一类随机时延网络化控制系统的容错控制研究[J].信息与控制,2006,35(5):384-387.
[3] 陈青,吴敏.具有网络丢包和时延的网络化控制系统设计[J].控制与决策,2011,26(2):293-296.
[4] 邵奇可,俞立,张贵军.网络时延在线估计技术与控制器的协同设计[J].自动化学报,2007,33(7):781-784.
[5] 陈雨,张颖伟,Joe Qin S.MIMO多输入输出网络控制系统的容错控制[J].清华大学学报:自然科学版,2007,47(s2):1844-1847.
[6] 张庆灵,张雪峰.网络化控制系统研究综述与前景展望[J].信息与控制,2007,36(3):364-370.
[7] 郭一楠,张芹英,巩敦卫,等.一类时变时延网络控制系统的鲁棒容错控制[J].控制与决策,2008,23(6):689-696.
[8] REN Jun,LI Chunwen,ZHAO Dezong.Fault-tolerant control of networked control system with time-varying transmission times[C]//Proeeedings of Sixth Intenational Conference on Machine Learning Cyberneties,HongKong,2007,8:101-108.
[9] ABERKANE S,SAUTER D,PONSART J C.Output systems feedback stochastic H1 stabilization of networked fault tolerant control[J].Journal of Systems and Cotrol Engineering,2007,221(6):84-89.
[10] 李炜,曹慧超.区间快变时延NCS鲁棒保性能容错控制[J].华中科技大学学报:自然科学版,2011,39(3):105-110.

