采用改进粒子群算法的无人机协同航迹规划

朱收涛， 曹林平， 翁兴伟， 董康生， 封普文

(空军工程大学航空航天工程学院，西安 710038)

0 引言

近年来，随着无人机技术的发展，各种无人机航路规划算法也得到了快速发展，目前存在的研究方法主要有动态规划算法、遗传算法(GA)、A*算法、蚁群优化算法(ACO)和粒子群(PSO)算法等。这些算法各有优势，并广泛应用于无人机的单机航迹规划中。然而，随着战争态势的发展，单机作战已不再适应战场需求，多无人机协同作战将成为主要的作战方式［1］。对于多架无人机来说，在规划航迹时除了要保证单架无人机的运动限制、安全性等因素外，还需要处理各无人机航路在时间、任务上的协调关系。因此，本文从解决多无人机协同航迹规划问题入手，提出了两种解决方案，然后主要针对空间直接解决法，进行了详细分析，最后结合一种改进的粒子群算法作了进一步的仿真分析。

1 多无人机协同航迹规划问题分析

多无人机协同航迹规划主要包括时间和空间上的协同［1－2］，即在研究多无人机协同航迹规划时，不仅要考虑到各无人机在时间上的协同到达(同时到达或在一定的间隔时间内到达)，还要重点考虑避免各无人机空间上的相互碰撞的问题。针对这一问题，解决的方法可以分为两种:一是空间上的直接解决;二是时间上的间接解决。空间上的直接解决主要是在规划无人机航迹时，使各无人机分布于不同的高度层，这样各无人机就只在属于自身的高度层飞行，结合相应的时间要求，进行多机协同航迹规划，执行所携带的任务。时间上的间接解决主要是在规划无人机航迹时，各无人机没有相应的高度空间限制，在满足自身约束限制和时间协同基础上的完全协同，使所规划的各无人机航迹在同一时刻不会出现交叉点(碰撞点)，从而协同完成任务。图1、图2为两种方法航迹规划示意图。

图1 空间直接法下多机协同航迹规划示意图Fig.1 Multi－UCAV cooperative path planning through direct space method

图2 时间间接法下多机协同航迹规划示意图Fig.2 Multi－UCAV cooperative path planning through indirect time method

2 协同变量与协同函数的构建

在航迹规划中，航迹的评价是极其重要的一部分。完整的航迹评价需要考虑影响无人机飞行的各种因素，并对各种因素进行量化，然后确定这些因素的影响权重，再进行综合计算和航迹的寻优操作。在研究无人机航迹规划时，由于雷达威胁和路径长度对无人机的评价有重要的影响，因此建立协同函数。

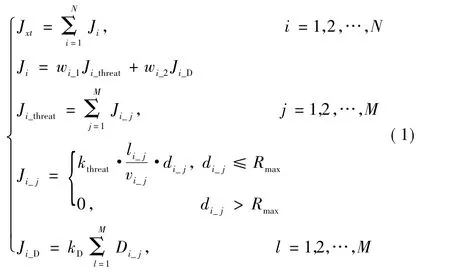
式中:Jxt表示N架无人机总的协同函数，为协同变量T的函数;Ji表示第i架无人机的代价函数;Ji_threat表示第i架无人机的雷达威胁代价;Ji_D表示第i架无人机的距离代价;wi_1表示第i架无人机威胁代价的权重;wi_2表示第i架无人机距离代价的权重，且有wi_1+wi_2=1;Ji_j表示第i架无人机第j条边的威胁代价;kthreat为威胁系数;li_j为第i架无人机第j条边经过雷达威胁区域AB段的距离;vi_j为AB段无人机的飞行速度;di_j为雷达中心O到AB段的距离;Rmax为雷达最大探测距离;kD为距离系数;Di_j表示第i架无人机路径中第j条边的长度，如图3所示。

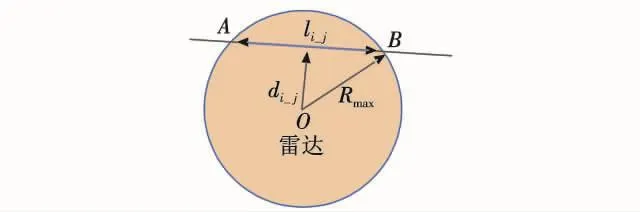
图3 雷达威胁示意图Fig.3 Threat of radar

多架无人机要能够协同作战，首先要实现信息的交融与共享。文献［3］在进行多无人机协同航迹规划研究时，提出了一种基于分解策略的协同算法，并引入编队预计到达目标时间ETA(Estimated Team Arrival time)作为协同变量，飞行航迹的代价作为协同函数，通过协同函数传递各架飞机到达目标的时间范围，最终通过在协同规划层调整ETA，寻找到既能满足时间约束，又能使团队代价最小，且尽量使单架无人机的个体代价次最小的航迹。文献［4］通过构建了多UCAV航迹规划的系统总体结构，并以协同时间作为指标建立协同管理层的思想，给出了多UCAV协同飞行时间的确定方法，最终利用相关算法进行了航路规划。这两种方法的主要思想是从计算出协同时间出发，然后利用算法得出航迹，本文基于此思想进行了改进，然后利用粒子群算法进行航路规划。文献［3－4］的方法流程如图4所示。

图4 协同变量计算流程图Fig.4 Flow chart of coordination variable calculation

由于无人机航路规划中选取的目标函数不同，所规划的最优路径不一定是最短路径。为了使最优路径等同于最短路径，对规划空间内的各类威胁加以处理，就是使所有的威胁固化(或硬化)，然后形成除威胁外的可行空间，使其规划的最优航迹等同于最短航迹。具体的处理方法是:硬威胁区域不变，软威胁进行威胁等效，威胁程度低于某一概率值时，处理为可行空间;威胁程度高于这一概率值时，处理为硬威胁，即不可行空间。图5a、图5b分别为避飞区和雷达威胁的硬化处理示意图，其中，A区域为硬化区域，B区域为可行区域。另外，本文假设所有无人机为同一类型的无人机，各无人机均以 v匀速飞行，其中，v∈［vmin，vmax］。

图5 避飞区和雷达威胁的硬化处理示意图Fig.5 Ossifying of no－flying area and radar

如图4所示，在进行各无人机到目标点的最短路径规划后，要判断是否存在交集，若存在，则选取编队协同变量t和对应的路径编号以及相应的飞行速度输出到对应的UCAV的路径规划层;若交集为空，路径规划层再为每个UCAV规划第2、第3最短路径，直到时间集合的交集不为空集。很明显，在交集为空时，还需要第2次甚至多次的判断才能寻找出协同变量t，然后找出相对应的路径。这样的话，规划时间就会有很大的不确定性，因此，需对此作以改进，其方法流程如图6所示。

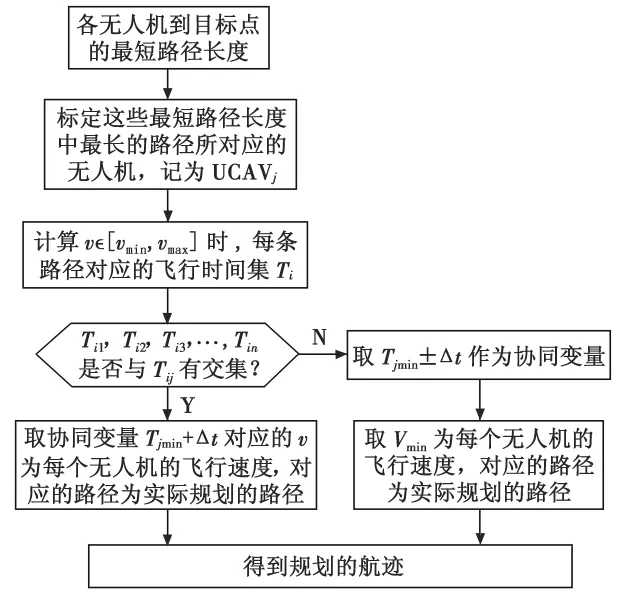
图6 改进后的协同变量计算流程图Fig.6 Flow chart of the improved coordination variable calculation

如图6所示，在得到各无人机到目标点的最短路径规划后，找出这些最短路径中的最长路径，并记该路径所对应的无人机为UCAVj，路径长度表示为Lj。

假设UCAVj的最短路径长度Lj为所有无人机最短路径集合中的最长路径，即 Lj=max{L1，L2，…，Lj，…，Ln}，n=1，2，…，N(N≥j)。在速度范围 v∈［vmin，vmax］已知条件下，对应的时间范围 Tij=［Tjmin，Tjmax］。相应的其他无人机在最短路径下所对应的时间范围为Tin=［Tnmin，Tnmax］，其中 n≠j，n=1，2，…，N。易得 Tjmin≥max Tnmin，可知，若其他各无人机与UCAVj所对应时间范围交集不为空，则须有

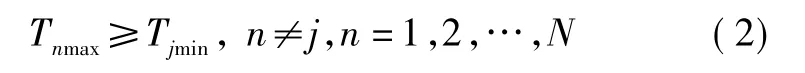
然后，进行其他各无人机与UCAVj所对应范围交集判断，若交集存在，则取协同变量Tjmin对应的v为此架无人机的飞行速度，对应的路径为实际规划的路径，后面直接保存，不再规划。若有其他的无人机与UCAVj所对应时间范围交集为空，则取Tjmin±Δt作为协同变量，Δt为同时到达允许误差，取Vmin为每个无人机的飞行速度，然后进行路径规划，得出相应的路径。

这里取Vmin为每个无人机的飞行速度，是因为该无人机与UCAVj所对应时间范围交集为空，则表示该无人机的最短路径长度太短，以致以Vmin飞行，所用的时间Tnmax仍小于Tjmin，进而形成交集为空。取Tjmin±Δt作为协同变量，只有以Vmin为每个无人机的飞行速度，其增加的路径长度ΔL最少，即所增加的将会代价最少。

3 粒子群算法

粒子群(PSO)算法从生物种群行为这种特性中得到启发并用于求解优化问题。在粒子群优化算法中，每个粒子都有自己的位置和速度，还有一个由被优化函数决定的适应值，并且知道自己到目前为止发现的最好位置(pbest)和现在的位置X。这个可以看作是粒子自己的飞行经验。除此之外，每个粒子还知道到目前为止整个群体中所有粒子发现的最好位置(gbest)(gbest是在所有pbest中的最好值)。其数学描述可以表示为

一般来说，为了节约管道资源，厨房和卫生间都会设计在一起。但是，由于厨房会产生大量的烟雾，所以要注意通风。首先要根据室内通风合理设置厨房的位置，这样厨房的烟就可以通过烟机和窗户迅速排出。其次，厨房设置为开放式或半开放式，以促进空气流通。

式中:Vi(t)为第i个粒子的速度;Xi(t)为当前第i个粒子的位置;w为惯性权重;pbest为个体极值;gbest为全局极值;rand()为介于(0，1)之间的随机数;c1，c2是学习因子。

虽然粒子群优化算法具有形式简单和性能高效的特点，但它也有一个缺陷，那就是容易陷入局部最优而早熟收敛。因此，本文运用一种基于自然选择的混合粒子群算法，以在后期对种群保持多样性，进而能够保证全局最优搜索的精度［5］。

将自然选择机理与粒子群算法相结合得到基于选择的粒子群算法［6－7］，其基本思想为每次迭代过程中将所有粒子按适应值排序，用群体最好的一半的粒子的速度和位置替换最差的一半的位置和速度，同时保留原来每个个体所记忆的历史最优值。将其运用到航迹规划中，每一个粒子代表一条航迹，其算法步骤如下:

1)随机初始化种群中各微粒的位置和速度;

2)评价每个微粒的适应度，将当前各微粒的位置和适应值存储在各微粒的pbest中，将所有pbest中适应值最优的个体的位置和适应值存储于gbest中;

3)更新每个微粒的速度和位置;

4)对每个微粒，将其适应值与其经历过的最好位置作对比，如果较好，则将其作为当前最好位置;

6)将整个粒子群按适应值排序，用群体最好的一半的粒子的速度和位置替换最差的一半的位置和速度，保持 pbest和 gbest不变;

7)若满足停止条件，搜索停止，输出结果，否则返回3)继续搜索。

一个粒子表示解空间中的一个可能解，即搜索空间中的一条备选航迹。航迹编码的本质是在种群中的每个粒子与搜索空间中的备选航迹之间建立一个一一映射关系。每个粒子代表唯一的一条航迹，每条航迹也对应唯一的一个粒子［8－9］。

种群可以表示为一个矩阵 X=［X1，X2，…，Xm］T，其中:m为种群的大小;Xi为种群中的第i个个体(i=1，…，m)。由于每条航迹有相同的起始点和目标点，所以起始点与目标点不参与粒子的编码。设每条航迹除起始点和目标点外由n个航迹节点组成，为了记录每个航迹节点的空间位置信息(x，y)，采用以下的定长实数编码粒子结构

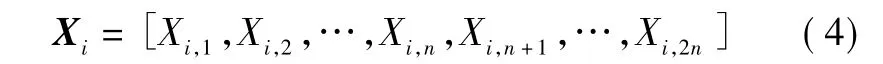
式中，Xi，1，Xi，2，…，Xi，n和 Xi，n+1，…，Xi，2n分别记录了 n个航迹节点在二维平面内的横坐标值x和纵坐标值y。基于上面的粒子结构，第i条航迹的第j个节点坐标为(xi，j，xi，j+n)，其中，j=1，…，n。

由于对威胁作了处理，算法运行时，只在可行区范围内进行，此时wi_1=0，所以单架无人机的代价函数Ji变为

然后由此计算多架无人机的总的协同函数Jxt。

4 仿真验证

为了减少无人机数据的计算量和信息的传输量，可由地面站直接为无人机编队规定合理统一的到达时间Td(Td≤Tjmax)，使各无人机在这一到达时间值的要求下，各自规划出最优的航迹，这就把模型简化成了在有时间要求下的无人机二维航迹规划。这里按照图6所示的方法进行仿真验证。

在构造二维规划空间时，雷达威胁模型(包括雷达、高炮和地空导弹等)可以等效为含有威胁等级的圆形区域，规划出具有突防效果的无人机航迹，具体威胁分布如图7所示。

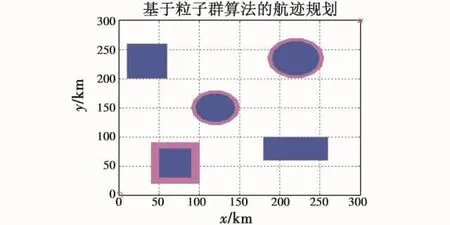
图7 航迹规划空间威胁分布图Fig.7 Threat distribution of path planning

如图7所示，在300 km×300 km规划空间内，起始点(0 km，0 km)，目标点(300 km，300 km)，威胁包含两处敌方防空雷达或武器威胁，两处矩形禁飞区，一处矩形避飞区。设无人机飞行 Ma 数为［0.6，0.8］，协同时间约束T=2100±15 s。结合混合粒子群算法，进行基于协同时间约束下的单航迹规划仿真实验。

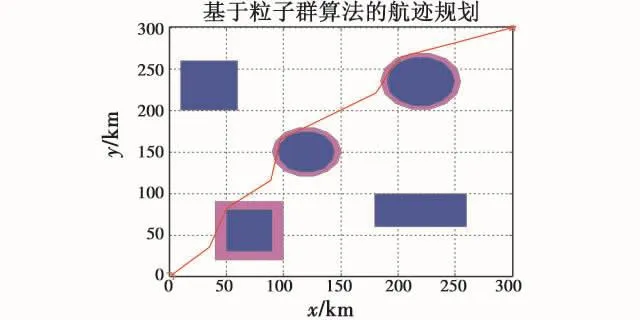
图8 具有时间约束的单机航迹规划图Fig.8 UCAV path planning with time restriction

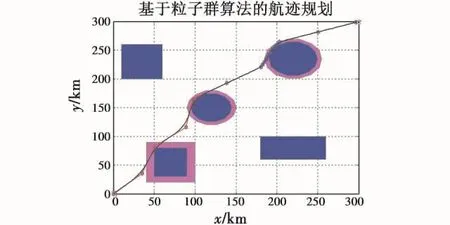
图9 经过平滑处理的航迹规划图Fig.9 UCAV path planning after smoothing

如图8所示，红色线条为所规划的航迹，其距离代价为550.25 km，经过平滑处理［7］后变为 546.128 km，以Ma为0.76匀速飞行，到达目标点时间为2113.6 s，满足协同时间约束的要求。为了使所规划的航迹更加符合无人机真实航迹，进行平滑处理，结果如图9中黑色轨迹所示。在进行多机协同航迹规划仿真实验时，协同变量按照图6所示的流程计算得出。假设有3架无人机，其起始点分别是(0 km，0 km)，(0 km，150 km)和(150 km，0 km)，目标点和规划环境如图7所示。初步规划结果如图10所示，为各无人机最短路径俯视图，其中UCAV1所规划的最短(最优)航迹为3架无人机中的最长航迹，假设UCAV1以Ma为0.8匀速飞行到目标点，则其用时2007.8 s。可得协同变量 T=2007.8 s，加上误差，则 T=2007.8 ±30 s。UCAV2最短航路长 420.5 km，其时间段为 T2=［1546.0 s，2058.8 s］，T2max＞T，则 UCAV2以 T 为协同变量，以该航迹为规划航迹，以Ma为0.6飞行即可满足要求。UCAV3最短航迹长度为362.3 km，该路径下其时间段为 T3=［1331.99 s，1776.0 s］，由于 T3＜ T，所以需要对UCAV3进行以Ma为0.6的飞行，在协同时间T=2007.8±30 s的约束下进行航迹重规划，即找出航迹长度在［403.5 km，415.7 km］的最优航迹。

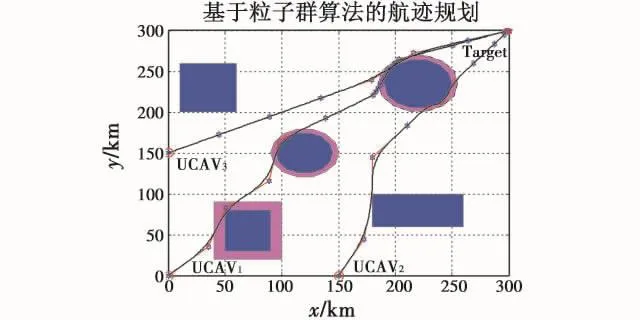
图10 不同高度层多无人机航迹规划俯视图Fig.10 Top view of multi－UCAV path planning at different height layers

因此，利用本文改进的方法进行规划，使无人机达到协同，仿真结果如图11所示。

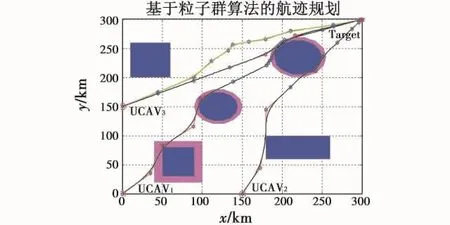
图11 不同高度层多机协同航迹规划俯视图Fig.11 Top view of multi－UCAV cooperative path planning at different height layers

寻找到UCAV3在规定范围内的最优航迹如图中绿色轨迹所示，为410.2 km，满足协同要求。

5 结束语

通过仿真验证，可以看出本文构建的协同变量和协同函数计算方法，使协同变量有了一定的确定性，进而提高了系统运算的速度。同时，提出空间直接法，较好地解决了多无人机协同航迹规划问题。仿真结果表明，该方法在多无人机协同航迹规划中具有较高的应用价值。

［1］ 黄长强，翁兴伟，王勇，等.多无人机协同作战技术［M］.北京:国防工业出版社，2012.

［2］ 任敏，王克波，沈林成.多UAV协同突防规划与仿真［J］.控制与决策，2011，26(1):157－160.

［3］ 安柏义.多无人机系统协同航迹规划［D］.南京:南京航空航天大学，2008.

［4］ 高晓光，符小卫，宋绍梅.多UCAV航迹规划研究［J］.系统工程理论与实践，2004，24(5):140－143.

［5］ 曹永恒.基于粒子群优化算法的船舶航迹规划方法研究［D］.上海:复旦大学，2010.

［6］ 龚存，王正林.精通MATLAB最优计算［M］.北京:电子工业出版社，2012.

［7］ POUR N E.Path planning of unmanned aerial vehicle using particles swarm optimization and B－spline curves［D］.Canada:Royal Military College of Canada，2009.

［8］ 傅阳光.粒子群优化算法的改进及其在航迹规划中的应用研究［D］.武汉:华中科技大学，2011.

［9］ HOLUB J S.Improving particle swarm optimization path planning through inclusion of flight mechanics［D］.Iowa:Iowa State University，2010.