构造法的应用

☉河南省偃师市教育局 李 郊

一、常用的构造方法

1.类比构造：由于问题中研究对象有着形式上、本质上的相同或相似，通过构造类似的数学形式，运用新数学形式的丰富内涵达到解决问题的目的.

2.归纳构造：对于与n有关的问题，不容易直接构造出，而以具体的特殊的如f（1）、f（2）、f（3）进而推进到f（n）等.

3.逆向构造：是指按逆向思维方式，向原有数学形式的相反方向去探求，通过构造（形式上、关系上或程度上）对立的数学形式来解决问题.

4.联想构造：联想是由一事物想另一事物的思维方式和过程，这种联想通常是事物的形式、结构、范围、关系等因素作用的结果.

二、解题方法指导

1.应用好构造思想解题的关键在于两点：一是要有明确的方向，即为什么目的而构造；二是要弄清条件的本质特点，以便重新进行逻辑组合.

2.在运用构造法时，还要注意以下两点：一是构造出的数学模型要保证能反映出原命题的本质特征；二是构造出的数学模型所获得的结果，一定是原命题的解题目标，并经过检验，对于不符合原命题解题目标的结果应予以舍弃.

三、范例剖析

例1 若非零向量a和b的夹角为120°，且|a|=2，|b|=5，则（2ab）·a=___________.

点拨：由于向量具有代数与几何的双重性，结合三角形法则与平行四边形法则构造平面图形，利用平面几何图形的直观性，可使问题得到巧妙、快捷的解答.

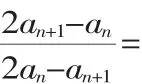
（1）求数列{an}的通项公式；

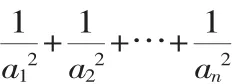
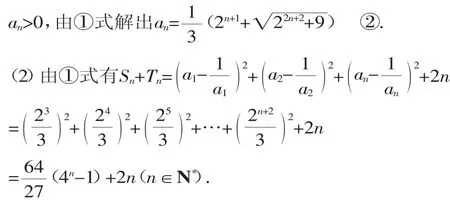
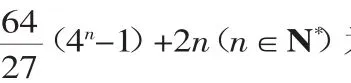
当n=1、2时，显然Sn+Tn不为整数.

当n≥3时，4n-1=（1+3）n-1=C1n×3+C2n×32+33（C3n+…+3n-3Cnn）.

点拨：数列是高中数学很重要的内容之一，蕴含着丰富的数学思想，尤其是递推数列问题具有很强的逻辑性，是考查逻辑推理和化归转化能力的很好素材.解答此类题的主要着眼点，一般是利用作差法、倒数法、迭代法、叠加法、换元法、待定系数法等转化等差数列或等比数列.

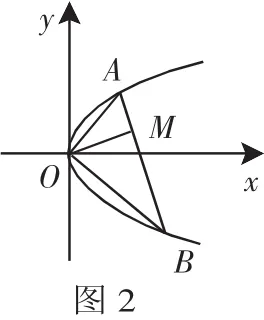
例3 如图2，设点A和B为抛物线y2=4px（p＞0）上原点以外的两个动点，已知OA⊥OB，OM⊥AB，求点M的轨迹.

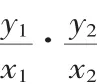
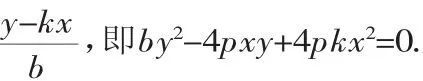
直线AB的方程可表示为y=k（x-4p） ①.

由①②消去k，得x2+y2-4px=0（x≠0）.

点拨：构造方程解题是一种重要的数学方法.在解答直线与圆锥曲线的问题时，一种常用的方法就是利用直线方程与圆锥曲线方程转化为关于x或y的二次方程，尤其是利用直线与圆锥曲线方程，构造出与x、y有关的二次齐次方程，可以有效地解决涉及斜率的积与和的问题.