引信解除保险距离兰利法试验最小样本量

叶美凤，王雨时，闻 泉

（南京理工大学机械工程学院，江苏 南京 210094）

0 引言

解除保险距离是引信的一项重要性能指标，对引信安全性、可靠性甚至于引信设计都有直接或间接的关系，因此引信解除保险距离测试显得至关重要。文献［1］推荐用于引信解除保险距离测试的方法包括概率单位法、兰利（Langlie）法、一次使用变换响应法（OSTR法）和勃罗西登（Up and Down）法（升降法）。其中兰利法以其变步长的试验机制，加快了试验数据向均值的收敛速度，减少了试验样本量N，因而节约了试验成本，提高了试验效率。但N的确定在现行标准中没有详尽规定。文献［1］“建议至少进行20发试验，或者经过含有混合结果区的5次响应变换。”

兰利法试验参数：均值μ和方差σ受N 影响比较大。一般认为N越大，μ和σ的极大似然估计精度就越高［2－3］。由于受限于试验成本和效率，所以应合理确定N。本文从理论上探讨此问题。

1 兰利法最小样本量研究理论基础

1.1 兰利法概述

兰利法最初用于估计50%响应点的激励值［1－2，4－6］。据此，假设引信解除保险距离服从正态分布。兰利法试验目的是估计正态分布参数μ和σ，进而估计任意响应点xp［7］。保证响应与不响应点个数相等［8－9］。

为区别于本文提出的试验方法，将文献［1］和［10］提出的兰利法称为传统方法。传统方法终止准则有两种：

1）完成预定的试验量N，并且试验数据含有混合结果区——全响应刺激量下限x1L和全不响应刺激量上限x0U满足x1L＜x0U。

2）完成响应与不响应转换的次数，并且试验数据也必须含有混合结果区。

1.2 满足μ、σ精度要求的最小试验次数

1.2.1 关于确定最小试验次数的几点说明

1）关于引信解除保险距离，GJB373A-1997《引信安全性设计准则》取置信度95%。

2）样本量至少为8［11－12］。兰利法试验样本量一般均少于100［3］。为了合理确定正态分布偏量修正系数及各变量参数，预定N取值范围为［8，100）。

3）假设样本方差λ＝S／σ，式中λ是S和σ的比例系 数。文 献 ［13］E3.9 S／σ ～ n 关 系 表 给 出：

4）假设η＝σ／μ。兰利法试验全响应刺激量上限xU和全不响应刺激量下限xL满足xL＝μ－kσ、xU＝μ＋kσ和k∈［2，4］时为兰利法最优的试验条4时，xL＝μ－kσ≥0，即0＜σ／μ≤1／4；当k＝5时，充分包含了总体临界刺激量，且4＜k≤5时，xL＝μ－kσ≤0［1－3，10，14］，则σ／μ≥1／5。综上，当1＜k＜5时，η理论范围1／5≤η≤1／4。

1.2.2 满足μ、σ精度要求的误差理论

引信解除保险距离兰利法试验获得靶距xi（i＝1，2，…，N）相互独立且服从正态分布。实际引信解除保险距离服从总体分布N（μ，σ2）的参数μ和σ均未知。对兰利法试验数据采用文献［10］和［11］中方法处理得到均值和方差的最大似然估计值近似认为总体均值极大似然估计中β为正态分布偏量修正系数，其值可查文献［10］表4-2。

1.2.3 检验最小样本量Nmin的检验样本量Nt引入的理论基础

为确定最小样本量Nmin，引入中间变量检验样本量Nt，目的是当Nmin≤Nt时，Nmin达到试验要求。

按文献［15］正态总体均值的假设检验公式，在置信度1－α下，子样样本分布已知，且子样与总体

2 兰利法最小样本量

2.1 确定最小试验次数N min的步骤

分析进行中的试验：

1）记录混合结果区最小试验次数N′min；

2）记录响应数ni＝0和1个数相同的试验次数N″min，且N″min≥N′min；

3）将开始进行μ精度和σ精度估计的最小样本量初取为N0min＝N″min；

4）当N＝N0min时，分析满足μ估计精度的最小试验次数N1min；

5）当N＝N0min时，分析满足σ估计精度的最小试验次数N2min；

6）综合分析N1min、N2min，确定最小试验次数Nmin＝ max（N1min，N2min）。

2.2 满足μ估计精度的最小试验次数N 1 min

当0.200 0≤E0（1）≤0.346 5时，预估检验样本量 N1t（1）的范围：

已知0.741 0＜λ＜0.926 6，1／5≤η≤1／4，α＝0.05，8≤ N ＜100，由式（6）得 max N1t（1）＝24.01，min N1t（1）＝4.63，即4.63≤ N1t（1）≤24.01。N1t（1）取整数，由于预定样本量 N ≤ N1t（1））（8≤ N＜100），因此8≤N1t（1）≤24。

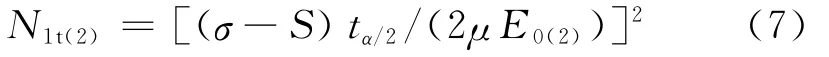
当0.021 6≤E0（2）≤0.027 1时，预估检验样本量 N1t（2）的范围：

已知0.741 0＜λ＜0.926 6，1／5≤η≤1／4，α＝0.05，8≤ N ＜100，由式（7）得 max N1t（2）＝12.56；min N1t（2）＝0.29，N1t（2）取 整 数，由 于 N ≤N1t（2）（8≤ N ＜100），因此，8≤ N1t（2）≤12。

3）由式（3）可知，E0（3）＝ ［（σ＋3S）Uα／2＋（σ－S）］tα／2／（4μ）。由于E0（2）＜E0（3）＜E0（1），因此0.027 1＜E0（3）＜0.200 0。满足μ精度的最小检验样本量N1t（3）的理论值公式为：

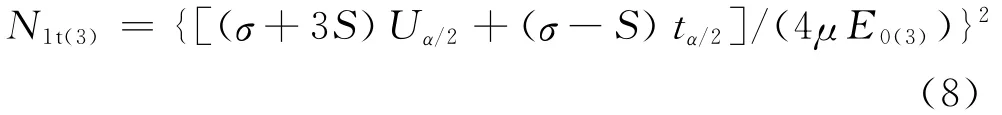
当0.027 1＜ E0（3）＜0.200 0时，预估检验样本量 N1t（3）的范围：

已知0.741 0＜λ＜0.926 6，1／5≤η≤1／4，α＝0.05，8≤ N ＜100，由式（8）得 max N1t（3）＝19.11；min N1tSt（3）＝0.18，N1t（3）取整数，由于 N ≤N1t（3）（8≤ N ＜100），因此，8≤ N1t（3）≤19。

4）由 式 （4）可 知 ，E0（4）＝ （Uα／2σ－tα／2S）／1／4，α＝0.05，8≤ N ＜100，得0.007 3＜E0（4）＜0.021 6。满足μ精度的最小检验样本量N1t（4）的理论值公式为：

当0.007 3＜ E0（4）＜ 0.021 6时，预估检验样本量 N1t（4）的范围：

已知0.741 0＜λ＜0.926 6，1／5≤η≤1／4，α＝0.05，8≤ N ＜100，由式（9）得 max N1t（4）＝12.66；min N1t（4）＝ 0，N1t（4）为 整 数，由 于 N ≤N1t（4）（8≤ N ＜100），因此，8≤ N1t（4）≤12。

5）由公式（5）可知，E0（5）＝ （S＋3σ）Uα／2／（2μα＝0.05，8≤N ＜100，由式（10）和E0（1）＜E0（5）得0.346 5＜E0（5）＜0.410 3。此时，满足μ精度的最小检验样本量N1t（5）的理论值公式为：

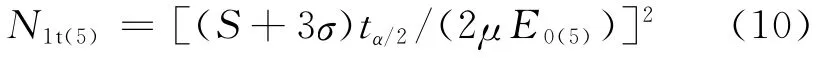
当0.346 5＜E0（5）＜0.410 3时，预估检验样本量 N1t（5）的范围：

已知0.741 0＜λ＜0.926 6，1／5≤η≤1／4，α＝0.05，8≤ N ＜100，由式（10）得 max N1t（5）＝11.22；min N1t（5）＝3.27，N1t（5）为 整 数，由 于 N ≤N1t（5）（8≤ N ＜100），因此，8≤ N1t（5）≤11。

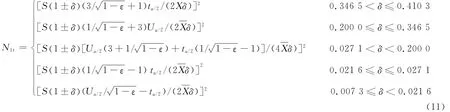
式（11）中，δ为均值μ精度，根据试验要求确定；ε为方差σ精度，根据试验要求确定。

2.2.3 满足方差σ条件的检验样本量Nt公式确定按1.2.3节，检验样本量Nt满足：

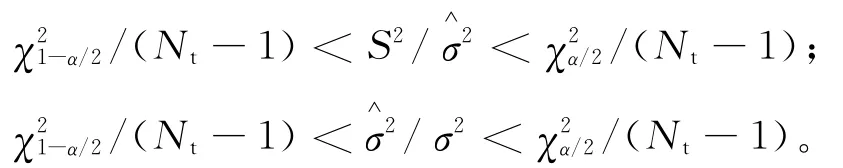
则 （σ2－S2）／σ2范围为：

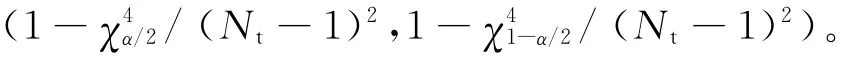
如果试验样本量 N ≤ N，则（σ2－S2）／σ2≤

t

2.2.4 满足方差σ精度要求最小检验样本量分析

总体方差σ在置信度1－α下，某两个数值范围内精度ε＝｜（σ2－S2）／σ2｜（0≤ε＜1），对ε的极值e0作如下分析：， ，

当8≤N＜100时，恒有＜σ2S2＜σ2因此

满足σ精度要求的最小检验样本量N2t的理论值公式为：

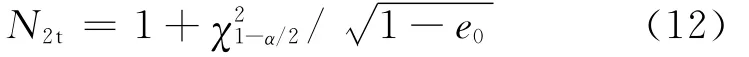
预估检验样本量N2t的范围：

由σ／S ＝λ（0.741 0 ≤λ ＜ 0.926 6），可 知0.141 4≤e0≤0.450 9。已知α＝0.05，8≤N ＜100，由式（12）得：2.82≤ N2t＜100.00。N2t取整数，由于预定样本量N≤N2t（8≤N＜100），故8≤N2t＜100。

由ε＝｜（σ2－S2）／σ2｜得，方差σ的估计值：

满足方差σ精度要求的检验样本量N2t公式如下：

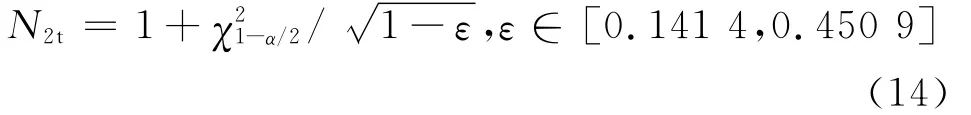
式中，ε为方差σ精度，根据试验要求确定。

2.2.5 最小样本量Nmin判定准则

准则1 如果N1t≤N0min，则μ满足试验精度要求，试验在N0min发结束，N1min＝N0min；反之μ不满足试验精度要求，N0min次试验后需增加i次试验。当恰好满足μ试验精度要求且响应ni＝0和1个数相等时试验结束，N1min＝N0min＋i（i＝0，1，2，…）。

准则2 如果N2t≤N0min，则σ满足试验精度要求，试验在N0min发结束，N2min＝N0min；反之σ不满足试验精度要求，N0min次试验后需增加j次试验。当恰好满足σ试验精度要求和响应数ni＝0和1个数相等时试验结束。N2min＝N0min＋j（j＝0，1，2，…）。

准则3 如果N1min≥N2min，则Nmin＝N1min；反之Nmin＝N2min。

兰利法试验或计算机模拟兰利法试验流程如图1所示。

3 案例分析

对某引信解除保险距离兰利法试验数据进行分析。试验按传统兰利法试验条件确定试验量N＝20。按兰利法最优的试验条件进行试验，预估刺激量下限xL＝20，上限xU＝60，均值μ≈40。试验结果如表1所列。

出现混合结果区的最小试验次数N′＝9；响应数ni＝1和0次数相同的试验次数N″min＝12、16和18；确定N0min＝12。最小样本量理论引入后兰利法数据处理方法及过程如下：

1）预设ε和δ，找出符合条件的N0min，分别进行均值μ和方差σ精度检验：

μ精度检验，取α＝0.05查文献［15-16］附表按不同精度选取式（11）确定N1min；

2）优越性比较。Matlab编程，分别对最小样本量理论引入后兰利法和传统兰利法，进行试验数据处理，并且检验试验数据是否满足：1＜k＜5。

3）最小样本量检验函数分段连续，取具有代表意义的点进行分析：ε＝0.450 9，δ＝0.100 0；ε＝0.141 4，δ ＝0.100 0；ε ＝0.250 0，δ ＝0.075 0。Matlab编程，μ精度检验时，选取式（11）计算N1t；σ精度检验时，按式（14）计算N2t。

4）确定兰利法试验最小样本量Nmin。传统兰利法数据处理结果见表3，最小样本量理论引入后兰利法数据处理结果见表2。

表1 某引信解除保险距离兰利法试验数据Tab.1 Datas of langlie method test of one f uze ar ming distance

表2 某引信解除保险距离兰利法试验数据最小样本量理论引入后分析结果Tab.2 Analyze on datas of the mini mu m nu mber of Langlie method test of f uze ar ming distance

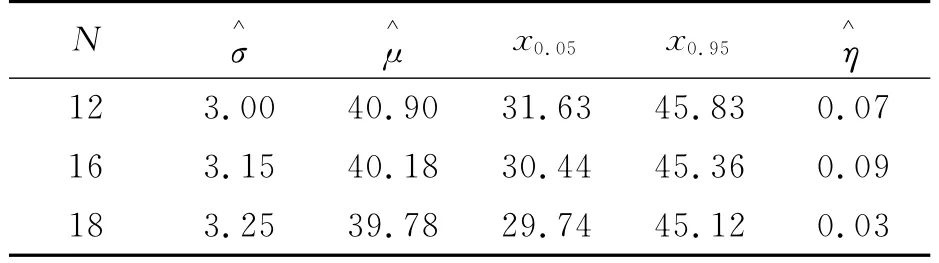
表3 引信解除保险距离传统兰利法试验数据分析结果Tab.3 Analyze on datas of the traditional langlie method test of one f uze ar ming distance

分析表2、表3可知按兰利法最优的试验条件xL＝μ－kσ、xU＝μ＋kσ，结果k∈（1，5），满足最小样本量理论引入后兰利法试验条件；随着试验样本量N的增加，一旦满足均值和方差σ精度，试验即可终止；试验样本量N对试验结果影响并不明显，均值μ的精度δ是影响试验结果的关键因素：精度δ越高，均值μ、方差σ及引信解除保险距离上、下限的估计精度越高，反之越低；精度δ较高时，能准确估计引信解除保险距离50%响应点；按式（13）求解方差σ，解除保险距离上、下限估计结果均比传统兰利法估计结果精度高，改善了传统兰利法试验拟合结果方差σ系统偏低、下限偏高及上限偏低的情况；理论上方差与均值之比η∈ ［1／5，1／4］，在均值估计几乎无偏时，最小样本量理论引入后的兰利法，方差与均值估计值之比η＇＜minη＝1／5，但偏小程度不明显；minη＝1／5，偏小程度很大，表明：最小样本量理论引入后方差估计值与理论值σ相比系统的偏低，但是偏低程度不明显。

4 结论

引信解除保险距离兰利法试验最小样本量范围［8，24］；引信解除保险距离95%和0.5%响应点、方差和均值估计精度并非随试验样本量增加而提高；试验响应点、标准差的估计受均值检验精度影响较明显；在均值精度选取较高时，能准确估计解除保险距50%响应点，且方差和引信解除保险距离上、下限的估计精度比传统兰利法高，改善了传统方法试验拟合结果方差估计偏低而下限偏高、上限偏低的情况。最小样本量确定后节约了试验成本和时间，获得标准差，引信解除保险距离上、下限估计值的最优解，但是依然无法避免标准误差估计系统偏低，从而导致引信解除保险距上限系统地偏小、下限系统地偏大的问题。

［1］西安机电信息研究所.GJB573 A-1998引信环境与性能试验方法［S］.北京：总装备部军标出版发行部，1998.

［2］严楠，田玉斌，蔡瑞娇.用计算机模拟法对Langlie试验程序的研究［J］.爆炸与冲击，1999，19（2）：108-114.YAN Nan，TIAN Yubin，CAI Ruijiao.Studies of langlie procedure by use of co mputer si mulation［J］.Explosion and Shock Waves，1999，19（2）：108－114.

［3］闻泉，王雨时.引信解除保险距离兰利法试验模拟研究［J］.兵工学报，2008，29（7）：774-780.WEN Quan，WANG YuShi.Si mulation f or langlie method test of f uze ar ming distance［J］.Acta Ar-mamentar II，2008，29（7）：774-780.

［4］钟海芳，田玉斌，蔡瑞娇.感度变量分布类型［J］.火工品，1998（3）：1-6.ZHONG Haifang，TIAN Yubin，CAI Ruijiao.Si mulation of the sensitivity response curve［J］.Initiator and Pyrotechnics，1998（3）：1-6.

［5］田玉斌，王典鹏，房永飞.火工品发火点估计方法比较研究［J］.含能材料，2010，18（1）：58-62.TIAN Yubin，WANG Dianpeng，FANG Yongfei.Co mparative study on estimating method of firing level of pyrotechnics［J］.Chinese Jour nal of Energetic Material，2010，18（1）：58-62.

［6］王雨时.感度用数理统计试验方法测定引信解除保险距离问题分析［J］.军用标准化，2006（3）：38-41.WANG YUshi.Analyzing problem on taking measure of f uze delay ar ming distance with mathematic statistical test method f or sensitivity［J］.Military Standardization，2006（3）：38-41.

［7］Mil-std-331c，depart ment of defense test method standar d：f uze and f uze co mponents，environ mental and perf or mance tests［S］.US：DOD，2005.

［8］宋锦泉，汪旭光.乳化炸药冲击波感度试验研究［C］／／中国力学学会.第七届工程爆破学术会议论文集.乌鲁木齐：新疆青少年出版社，2001：40-44.

［9］严楠，蔡瑞娇.序贯感度试验的设计原理［J］.火工品，2001（2）：40-44.YAN Nan，CAI Ruijiao.The design principle of sequential sensitivity experi mental procedure［J］.Initiator and Pyrotechnics，2001（2）：40-44.

［10］刘宝光.敏感性数据分析与可靠性评定［M］.北京：国防工业出版社，1995.

［11］北京理工大学应用数学系.GJB／Z377 A-1994感度试验用数理统计方法［S］.北京：国防科学技术工业委员会，1995.

［12］GB／T4882-2001数据的统计处理和解释正态性检验［S］.北京：国家质量技术监局，2001.

［13］GJB1853-1993反装甲弹试验方法［S］.北京：国防科学技术工业委员会，1994.

［14］洪东跑，赵宇，温玉全.基于序约束的火工品可靠性试验数据分析［J］.含能材料，2008，16（5）：556-559.HONG Dongpao，ZHAO Yu，WEN Yuquan.Order restricted analysis of reliability tests for explosive initiator［J］.Ener getic Matericals，2008，16（5）：556-559.

［15］陈萍，李文，张正军，等.概率与统计［M］.北京：科学出版社，2002.

［16］花成，张盛国.兰利法方差与可靠度估计影响因素研究［C］／／中国航空学会.中国航空学会可靠性工程专业委员会第十届学术年会论文集.北京：中国航空学会，2006：228-232.