基于自适应重采样的同步定位与地图构建
曲丽萍,王宏健,边信黔
(1.哈尔滨工程大学自动化学院,黑龙江 哈尔滨 150001;2.北华大学电气信息工程学院,吉林 吉林 132021)
0 引言
移动机器人同步定位与地图构建(Si multaneous Localization And Mapping,简称SLA M),是指机器人在自身位置不确定条件下,在部分已知或完全未知环境中运动时,根据位置估计和传感器数据进行自身定位、同时建造增量式地图[1-2]。
SLAM问题研究中,应用较多的是扩展卡尔曼滤波(EKF)SLAM和粒子滤波SLAM解决方案。EKF利用非线性函数泰勒展开式的一阶偏导部分(忽略高阶项),常常导致在状态的后验分布的估计上产生较大的误差,影响滤波算法的性能。另外,EKF算法要求状态的概率密度函数满足高斯分布,但实际系统往往是非高斯、非线性的(即系统状态/量测模型是非线性的,模型/量测噪声不服从高斯分布)。
对于非线性、非高斯系统的状态估计问题,比较有发展前途的是基于序贯蒙特卡罗方法和SIS的粒子滤波方法。该方法对系统噪声没有任何限制,它通过预测和更新来自于系统概率密度函数的采样集来近似非线性系统的随机贝叶斯估计。粒子滤波方法的优点是采样集中在高概率的区域,采样计算的过程也很简单,是一种非线性、非高斯系统的贝叶斯估计[2]。
但是,粒子滤波SLAM在进行机器人路径估计和路标位置估计过程中,经过几次迭代,粒子的权值会集中到少数粒子上,使得大量的计算工作都被浪费在用来更新那些对估计几乎不起作用的粒子上,这就是粒子退化问题,粒子滤波SLA M中的最经典的算法Fast SLA M也不例外。解决粒子退化问题的主要方法就是重采样。过频地重采样将增加计算负担,过少地重采样又会导致效率降低。
针对粒子退化和重采样问题,本文对最具代表性的Fast SLA M算法进行了改进,提出了基于自适应重采样的Fast SLA M方法。
1 移动机器人SLAM算法
1.1 移动机器人SLAM问题数学描述
移动机器人SLA M问题描述如图1所示。
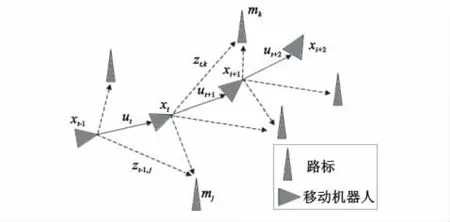
图1 移动机器人SLAM系统Fig.1 State of mobile robot SLA M system
假设机器人在未知环境中移动,同时使用自身携带的传感器探测外部未知的路标信息和获取自身的位姿信息(即机器人的位置和方向)。Xt表示t时刻移动机器人的位姿状态向量,mk表示第k个路标的位置状态向量,ut为机器人从t-1时刻到t时刻的输入控制向量,zt为t时刻传感器观测向量,t时刻机器人的系统状态(包含t时刻机器人位姿和路标位置)记为st,即st= {Xt,mt}。从概率学来看,假定移动机器人运动到当前位置并进行观测,则系统当前状态与之前的系统状态、观测信息以及输入有关,即 p (st|s0:t-1,z0:t,u1:t)[3]。假设系统当前的状态仅与前一时刻的系统状态和当前的输入有关,即前一时刻的系统状态已经包含了之前的系统状态、观测信息和输入,则当前系统状态的分布概率为:
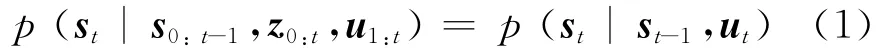
在此系统状态估计上获得的观测信息的估计为
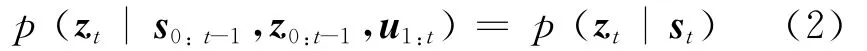
1.2 基于扩展卡尔曼滤波 (EKF)的移动机器人SLAM算法
1.2.1 联合状态向量动态模型
SLA M问题中的状态向量Xk,包括机器人的位姿Xrk和环境特征的位置Xmk,由于特征地图是静止状态,k-1和k时刻特征地图的状态相等,故基于扩展卡尔曼滤波的移动机器人SLA M算法的联合状态向量的动态模型为
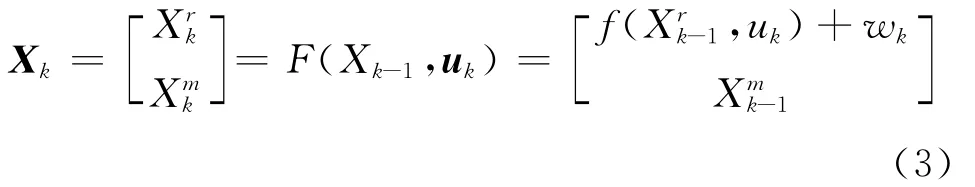
式(3)中,F(·)为联合状态转移函数,f(·)为移动机器人运动模型[4]。
1.2.2 基于扩展卡尔曼滤波的移动机器人SLA M算法
EKF是非线性系统均方差估计方法,假设状态向量Xk,观测量序列z1:k= [z1,z2,…,zk]T,则状态向量的最小均方差估计为:
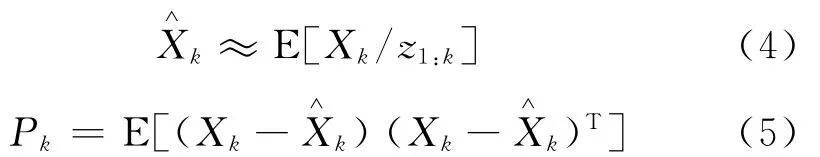
式(4)、式(5)中,所处理的变量假设服从高斯分布,用均值和方差表示为:
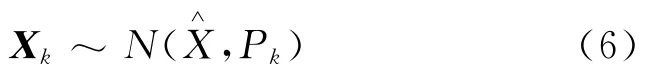
过程噪声wk和外部传感器的观测噪声nk认为是均值为零、方差分别为Qk及Rk的高斯白噪声。
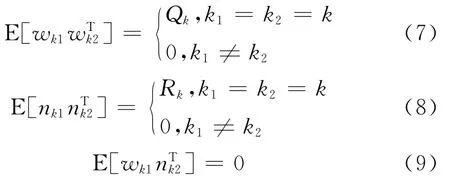
1.3 Rao-Blackwellise粒子滤波器
Mur phy等人对动态贝叶斯网络(Dynamic Bayesian Net wor ks)进行分析得出结论:若机器人的路径估计己知,则路标估计 (mi,mj,i≠j)之间相互独立。由贝叶斯公式及特征估计之间的独立性假设,对后验概率分布p(x1:k+1,m|z1:k+1,u0:k,x0)分解:
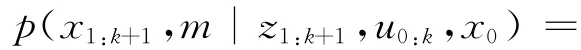
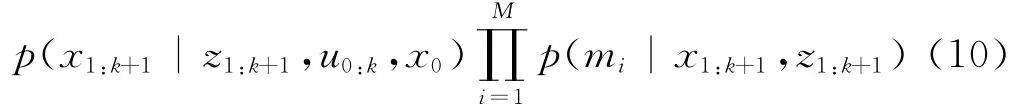
式(10)描述了Rao-Black wellise粒子滤波器思想,即首先将机器人路径和地图的联合估计问题分解为机器人路径估计和地图估计两部分,然后再将地图估计再分解为M(特征的数目)个相互独立的特征估计。
在粒子滤波器中,变量x的概率分布p(x)用带权重的粒子集表示,即

式(11)中,xi为第i个粒子,wi为第i个粒子的归一
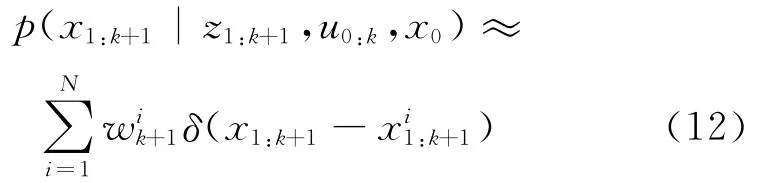
式(12)中,δ(·)是迪拉克函数,xi1:k+1表示第i个粒子的机器人路径,wik+1是第i个粒子的权值。如果可以直接从p(x1:k+1|z1:k+1,u0:k,x0)中产生粒子,则所有粒子皆赋予相同权值1/N。但一般来讲,p(x1:k+1|z1:k+1,u0:k,x0)是未知的,所以假定一个近似后验概率分布的提议分布q(x1:k+1|z1:k+1,u0:k,x0),然后从这个提议分布产生粒子,并按照下式赋权值:
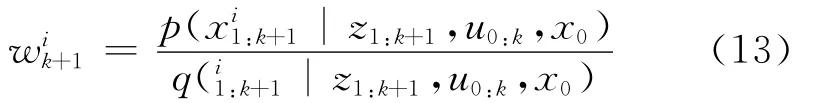
1.4 Fast SLAM算法的重采样
2 基于自适应重采样的Fast SLAM算法
目前广泛使用的Fast SLA M算法,是采用Rao-Black wellise粒子滤波器估计机器人路径,采用扩展卡尔曼滤波器估计地图。Fast SLA M在系统状态估计过程中,不可避免地会出现粒子退化问题。解决粒子退化问题主要方法是重采样。过频地重采样将增加计算负担,过少地重采样又会导致效率降低。因此,寻求一种适当的重采样方法,对于Fast SLA M的应用研究至关重要。
2.1 自适应重采样方法
Fast SLA M算法的基础是粒子滤波,粒子滤波的基本思想是利用序列重要性采样(SIS)的概念近似,用一系列离散的带权重的随机样本近似相应的概率密度函数[6]。当用重要性函数替代后验概率分布作为采样函数时,理想情况是重要性函数非常接近后验概率分布,也就是希望重要性函数的方差基本为零。即
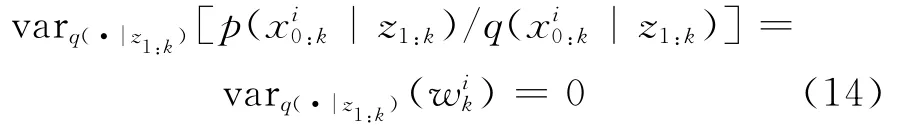
但是由于粒子滤波选择先验概率密度作为重要密度函数,没有考虑当前的量测值,从重要性概率密度中取样得到的样本与从真实后验概率密度采样得到的样本有很大偏差,尤其当似然函数位于系统状态转移概率密度的尾部或似然函数呈尖峰状态时,这种偏差更明显。因此,重要性权重的方差随着时间而随机递增,使得粒子的权重集中到少数粒子上,出现了粒子退化问题[7]。
增加粒子数目NS可以解决退化问题,但会使得计算量上升,影响算法的实时性。普遍采用的方法是重要性样本的重采样。重采样是一个减小无效样本,增加有效样本的方法,即舍弃“坏”的样本(具有小的重要性权值)、复制“好”的样本(具有较大的重要性权值)以适应系统的动态变化。但过频地重采样将增加计算负担,过少地重采样又会导致效率降低[8]。
本文采用的是自适应重采样方法:
1)计算有效抽样尺度Neff,确定粒子退化程度。
Neff定义为 Neff= NS/(1+varq(·|z1:k)())≤NS,但实际中无法按照上式确切计算Neff数值,所以通过式(15)近似估计:
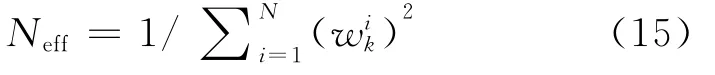
Neff越小,意味着退化现象越严重。
2)设定有效样本数阈值,实施自适应重采样
设定有效样本数Nthreshold=0.75 Nparticle作为阈值(其中Nparticle为粒子个数),当Neff<Nthreshold时,进行重采样,这样就实现了自适应地根据样本情况决定是否进行重采样,在一定程度上降低了算法复杂度。
自适应重采样方法,保证了只在必要时才进行重采样,有效减少了重采样次数,提高了Fast SLA M改进算法的鲁棒性。
2.2 基于自适应重采样的Fast SLAM算法
1)移动机器人位姿预测
根据控制向量uk、机器人运动模型,预测机器人k+1时刻的位姿分布,即计算各个粒子的位姿向量
2)特征地图路标数据关联
采用极大化观测概率函数的数据关联方法,将可观测到的观测信息(激光测距传感器可达到的范围内的路标)和各个粒子k时刻的估计地图依次进行数据关联。
3)采用自适应重采样,提高计算精度和效率
按照式(15)计算有效粒子数Neff,当Neff<Nmin(Nmin取0.75 Nparticle,Nparticle为粒子个数),说明粒子退化严重,则转入第4)步进行重采样;否则直接转至第5)步。
4)需要重采样时,获取提议分布并采样
根据各个粒子的关联观测信息,采用EKF对粒子的先验分布p(xk+1|,uk)进行观测更新,计算各个粒子的位姿向量在k+1时刻的滤波值和方差,得到各个粒子的提议分布q(x1:k+1|,zk+1,uk)。
5)机器人路径估计
采用Rao-Black wellise粒子滤波器估计机器人的路径,获取k+1时刻机器人路径后验概率分布
6)更新地图估计
根据各个粒子的关联观测信息,采用EKF更新各个粒子k+1时刻的关联特征估计,计算各个特征的估计均值和方差,对于没有和地图中的已有特征关联上的观测信息,则将对应的观测特征作为新特征加入地图。
3 仿真实验及结果
3.1 仿真设计
仿真环境:在200~250 m的仿真环境中设置机器人运动路径和135个路标,机器人的运动路径通过设定关键点人为设定,机器人从坐标(0,0)开始逆时针运行,机器人运动速度为3 m/s,最大转角30°,控制信号时间间隔为0.025 s,速度噪声为0.3 m/s,观测最远距离30 m,观测的间隔时间为0.2 s,观测距离噪声为0.1 m,观测角度噪声为1。
仿真任务:通过EKF-SLAM 及Fast SLA M2.0编程运行,估计机器人运动轨迹路径及周围路标位置。
3.2 仿真实验
3.2.1 本文运动模型
考虑到移动机器人是通过控制其左、右轮的正反转实现前进、转向等动作,所以当将一个控制量ut(前向速度和角速度)施加到机器人时,机器人运动的预测状态模型为[9]:
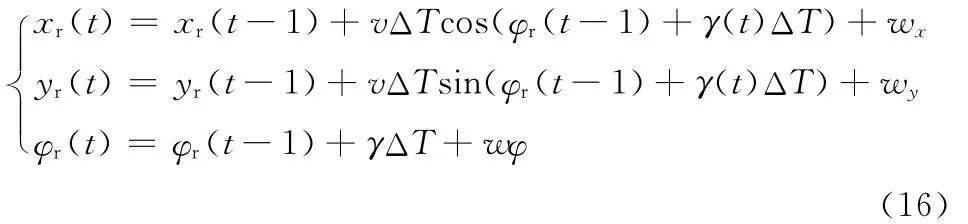
式(16)中,(xr(t),yr(t))和φr(t)为t时刻机器人的位置与方向角,v为机器人的运动速度,γ为角速度,wxyφ∈N(0,σxyφ)为均值为零的加性高斯噪声项,用于描述各种未知因素对机器人运动产生的影响。
假设环境路标是静止的,故环境路标的状态各时刻保持不变,即
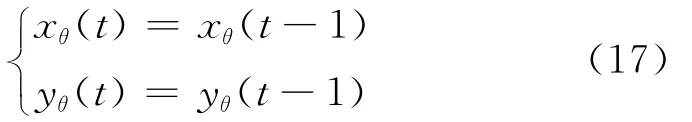
3.2.2 本文观测模型
考虑到机器人利用自身携带传感器探测路标,得到路标的距离和方向角,故观测模型可表示为[5]:
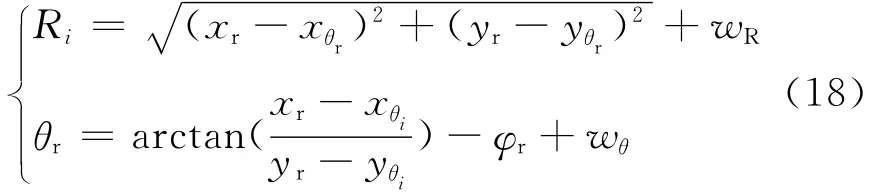
式(18)中,(xr,yr)为机器人的位置坐标,(xθi,yθr)为路标i的位置坐标,wR和wθ是测量距离和角度的噪声序列,且符合N(0,σR)和N(0,σθ)的高斯分布。
3.3 仿真结果
针对上述仿真实验,选取Matlab7.0运行环境,分别采用本文提出的两种算法,对机器人运动路径和环境路标进行了仿真估计,仿真结果如图2—图5所示。图2和图3为两种算法仿真结果,细实线为移动机器人设定路径,粗实线为仿真估计路径。图4为两种算法路标位置估计误差曲线。图5为两种算法机器人路径估计误差曲线。
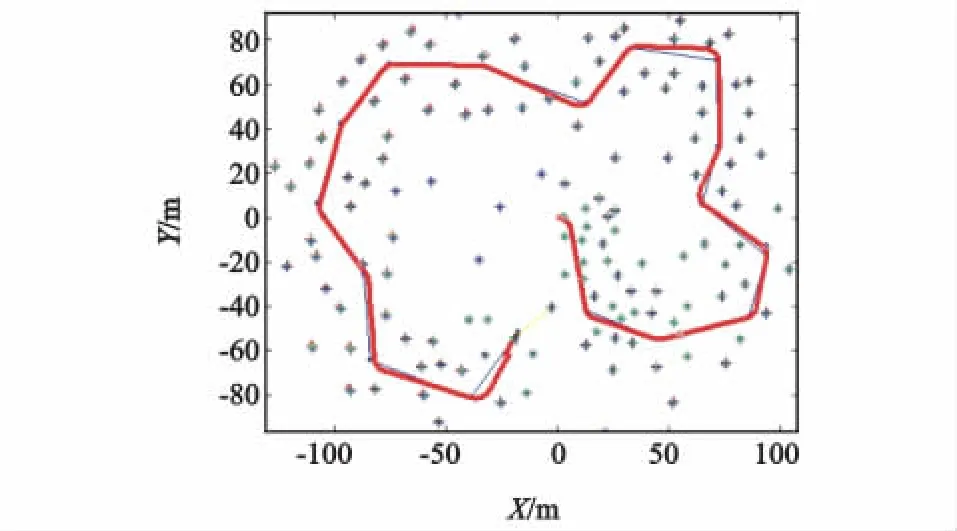
图2 基于EKF的SLAM应用算法的仿真结果Fig.2 Si mulation result f or si mulators based on EKF
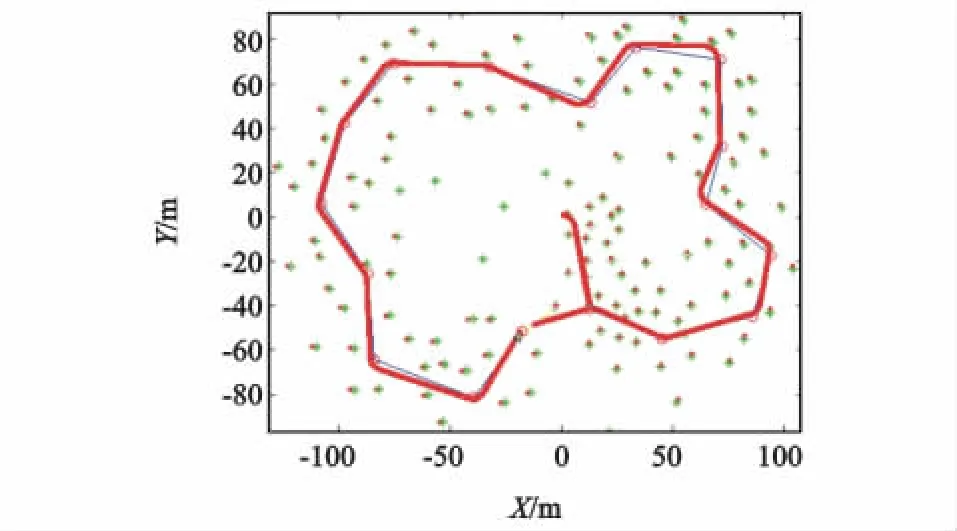
图3 基于自适应重采样Fast SLAM的仿真结果Fig.3 Si mulation result for si mulators based on adaptive resample fast SLAM

图4 基于EKF和基于Fast SLA M的SLA M应用算法的路标误差对比图Fig.4 Land mar k Error Result for Si mulators Based on EKF and Based on Adaptive Resample Fast SLA M
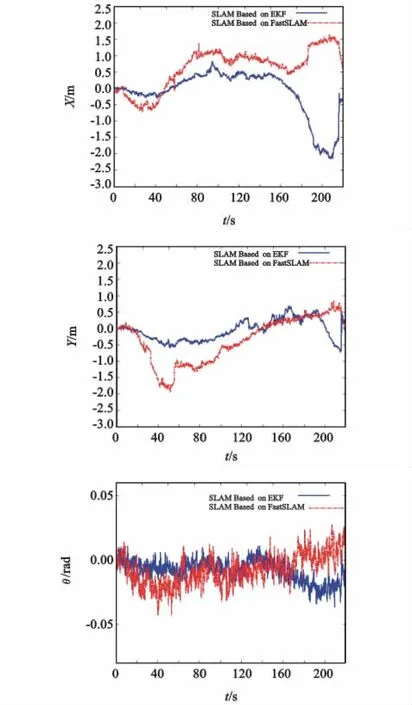
图5 基于EKF和基于自适应重采样Fast SLA M的SLAM应用算法的机器人路径X向,Y向及方向角误差对比图Fig.5 Vehicle error result f or si mulators based on EKF and Based on Adaptive Resample Fast SLA M
由图2可以看出,在路标位置估计方面,基于自适应重采样Fast SLAM算法较基于EKF的SLA M应用算法,估计的路标位置与设定的路标点重合的程度更好一些,即路标估计精度更高;在机器人运行路径估计方面,前者较后者误差更小一些,具有更高的精度。
4 结论
本文提出了基于自适应重采样Fast SLA M算法,该算法首先计算粒子集的有效样本数,确定粒子退化程度。然后设定有效样本阈值,当有效样本数小于阈值时则进行重采样。
仿真表明,EKF-SLA M和基于自适应重采样Fast SLA M两种算法都能完成机器人运动路径和路标地图的估计,但由于后者能够根据系统观测量信息获取更加符合的提议分布,且重采样的效率更高,算法鲁棒性更好。不但具有非线性、非高斯的普遍适用性,在机器人路径和路标位置的估计上,也具有更高的精度。
[1]Durrant-Whyte H,Bailey T.Simultaneous localization and mapping(SLA M):part I essential algorith ms[J].IEEE Robotics and Automation Magazine,2006,13(2):99-108.
[2]Durrant-Whyte H,Bailey T.Si multaneous localization and mapping(SLA M):part II state of the art[J].IEEE Robotics and Auto mation Magazine,2006,13(3):108-117.
[3]陈白帆,蔡自兴,袁成.基于粒子群优化的移动机器人SLAM 方法[J].机器人,2009,31(6):513-517.CHEN Baifan,CAI Zixing,YUAN Cheng.Mobile robot slam method based on particle swar m opti mization[J].Robot,2009,31(6):513-517.
[4]Wang Y M,Yang JB,Xu DL.A preference aggregation method through the esti mation of utility intervals[J].Computers and operations research,2005(32):2 027-2 049.
[5]邹智荣,蔡自兴,陈白帆,等.移动机器人SLA M中一种混合数据关联方法[J].小型微型计算机系统,2011,32,(7):1 341-1 343.ZOU Zhirong,CAI Zixing,CHEN Baifan.Hybrid appr oach of data association in mobile robot SLA M[J].Journal of Chinese Computer Systems,2011,32,(7):1 341-1 343.
[6]张海强,窦丽华,陈杰,等.典型场景下EKF-SLA M 估计一致性分析[J].北京理工大学学报,2011,31(10):1 194-1 202.ZHANG Haiqiang,DOU Lihua,CHEN Jie,et al.Consistency analysis of EKF-SLA M for a basic scenario[J].Journal of Beijing Institute of Technology,2011,31(10):1 194-1 202.
[7]周武,赵春霞,沈亚强,等.基于全局观测地图模型的SLA M 研究[J].机器人,2010,32(5):627-654.ZHOU Wu,ZHAO Chunxia,SHEN Yaqiang,et al.SLA M research based on global observation map model[J].Robot,2010,32(5):627-654.
[8]厉茂海,洪炳熔,罗荣华.用改进的 Rao-Black wellized粒子滤波器实现移动机器人同时定位和地图[J].吉林大学学报(工学版),2007,37(2):401-406.LI Maohai,HONG Bingrong,LUO Ronghua.Impr oved rao-black wellized particle filters f or mobile robot si multaneous localization and mapping[J].Jour nal of Jilin University(Engineering and Technology Edition),2007,37(2):401-406.
[9]夏益民,杨宜民,一种利用模糊逻辑改进Fast SLA M 2.0的方法[J].计算机工程与应用,2010,46(33):233-238.XIA Yi min,YANG Yi min.Improved Fast SLA M 2.0 algorit h m based on f uzzy logic[J].Co mputer Engineering and Applications,2010,46(33):233-238.

