AWGN信道EBPSK系统解调性能分析

常 虹 丁佳佳 吴乐南

(东南大学信息科学与工程学院，南京 210096)

由于信息传输系统不断宽带化，导致了无线电频谱的日益紧缺，由此更高效的调制技术受到了通信界关注.EBPSK是一类不对称的二元相移键控调制技术，通过小角度、小时段调相以集中信号频谱［1-2］;而解调则可采用特殊的滤波器将调相转变为调幅作为最后判决的依据，称之为冲击滤波器(impacting filter)［3-4］.目前对于 EBPSK 系统解调性能的研究多限于仿真，理论分析虽有些进展，但并未给出严格的数学证明，且未得到更严格的误比特率(BER)公式.文献［5］给出了一般意义下的EBPSK系统抽样判决的误比特率公式(即未确定冲击滤波器的系数以及零极点的个数)，但没有对误比特率公式进行数学上的证明和推导，对于1调制信号给出的误比特率函数不够严格，所推导得到的误比特率公式与仿真结果存在较大的差异.文献［6］在文献［5］所得的误比特率公式基础之上，通过改变滤波器零极点的个数和冲击滤波器的系数来比较抽样判决误比特率公式的差异性，由一般性转向特殊性分析.文献［7］给出了调制信号通过确定了具体系数后的冲击滤波器的时域全响应公式，并与仿真结果进行了拟合.

本文结合文献［7］的理论结果分析了暂态响应对于判决的重要影响，从而利用暂态响应对误比特率公式进行修正.其次对滤波信号分别收集抽样判决和积分判决后的样本集合，运用Matlab工具得到了此时信号0和1的概率密度函数(probability density function，PDF)曲线.通过对整个EBPSK调制解调机理的分析，推导出了解调信号0和1的PDF理论表达式，并与仿真曲线进行了回归拟合，估计由此得到连续情况下系统抽样判决和积分判决的误比特率公式，并与仿真情况下的误比特率进行了性能对比.

1 EBPSK调制方式与解调滤波器

1.1 EBPSK 调制

设g0(t)和g1(t)分别表示发送信息为0和1时的调制波形，则EBPSK调制定义如下:

式中，fc为载波频率;A，B为载波幅度;T为码元周期;τ为1码元的调制时间长度;θ为信号1的调制相位.设T内有N个载波周期，其中K＜N个被调制，则

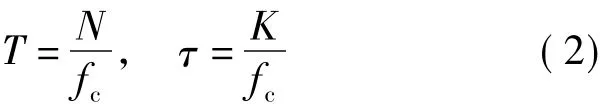
当θ=π时，τ=T，即为经典的BPSK调制;B=A且τ=T/4，即为脉位反相键控(pulse position phase reversal keying，3PRK)调制［8］;B=0，得到缺周期调制(missing cycle modulation，MCM)［8－9］.

可见经典的BPSK调制和美国最重要的超窄带调制均为式(1)的特例，故本文对于EBPSK解调性能的研究具有重要的理论和应用背景.

1.2 EBPSK解调滤波器

为了提高解调性能，针对式(1)K＜N的特点设计了冲击滤波器［3］，可在EBPSK调制信号的相位跳变处产生明显的冲击波形，把相位变化转变为幅度变化，以突出解调信号的差异性，得到比基于锁相环的EBPSK 解调器［8，10］更明显的鉴相特性.本文采用了幅频响应(见图1)具有单对共轭零点、2对共轭极点的滤波器，其系统函数为

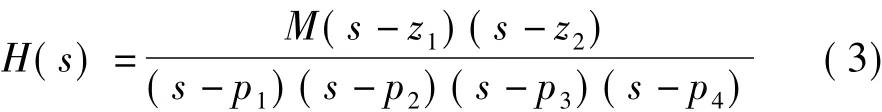
式中，z1，z2为一对共轭零点;p1，p2，p3，p4分别为 2对共轭极点;M为系统函数归一化常数.

图1 冲击滤波器幅频响应

文献［7］推导得到EBPSK调制信号的冲击滤波响应在未加噪声的情况下，发送比特0的EBPSK调制信号g0(t)通过冲击滤波器响应为

而发送比特1的EBPSK调制信号g1(t)通过冲击滤波器的响应为

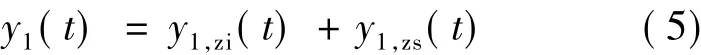
式中，y1，zi(t)为稳态响应，其表达式为

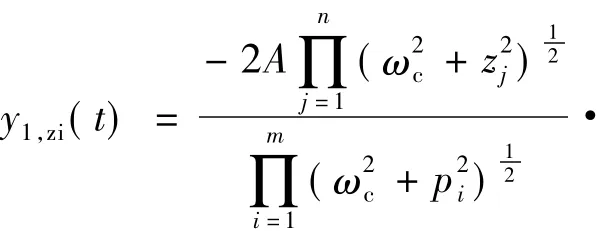
y1，zs(t)为暂态响应，其表达式为

式中，m为极点个数;n为零点个数.图2为EBPSK信号通过冲击滤波器后其理论表达式和仿真结果的比较，由图可见，滤波器对g0(t)，g1(t)响应的理论表达式与仿真结果趋于一致.

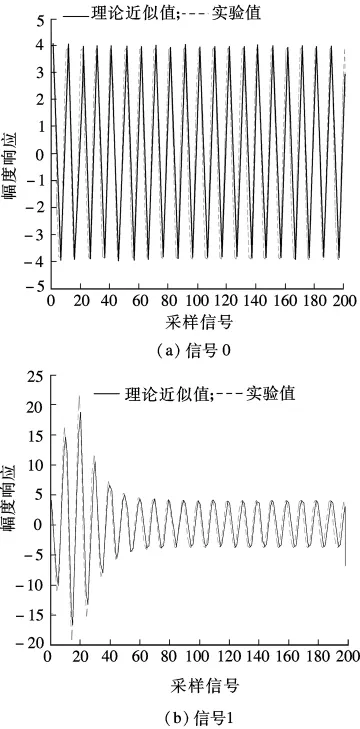
图2 信号通过冲击滤波器后理论和仿真结果比较

2 EBPSK检测模型

2.1 抽样判决

设含噪接收信号经冲击滤波器后输出的解调信号为

式中，n(t)为加性高斯白噪声(AWGN)通过冲击滤波器后的时域响应.若高斯白噪声的方差为σ20，则n(t)的方差为

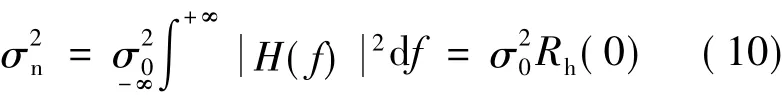
将式(3)的冲击滤波器转移函数经拉普拉斯反变换为其冲激响应，即

式中，m=4，n=2.现求其自相关函数表达式，为简化先假设其指数对应的系数分别为K1，K2，K3，K4，因为其形式比较复杂，但只要确定了冲击滤波器，这些系数就相当于复常数.于是式(11)的冲激响应简化为

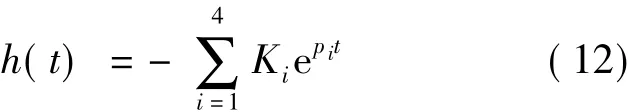
式中

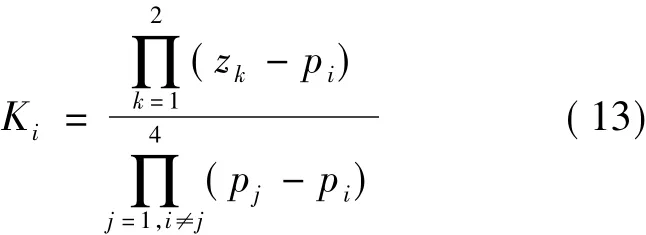
则自相关函数为

于是得到

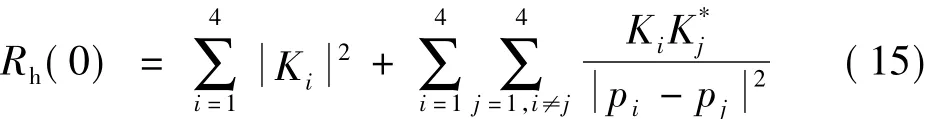
从而对于待解调信号0，式(8)成为

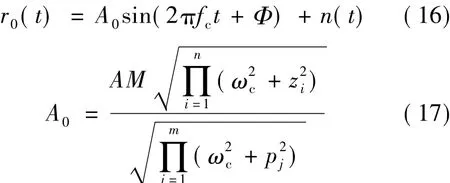
由于冲击滤波器带宽很窄，可以将n(t)建模为窄带高斯白噪声［11］，因而r0(t)的包络服从广义瑞利分布(即广义瑞利分布)［5］，其 PDF为

将式(19)与由抽样信号集合经Matlab仿真所得PDF比较见图3(a).而对于待解调信号1，由于其时域冲击响应为一分段函数，因此将其分段讨论.

1)在0≤t≤τ范围内

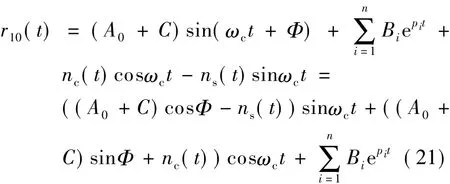
2)在τ＜t≤T范围内

同时将窄带高斯白噪声改写为

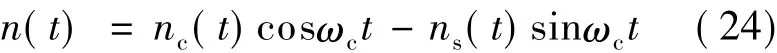
找到使得信号1冲击最高的时刻，记为ttop.由于r10(t)描述的是正弦振荡的建立与消失过程，故其幅度在0≤t≤τ内能够取得最大值，其包络服从改进的广义瑞利分布

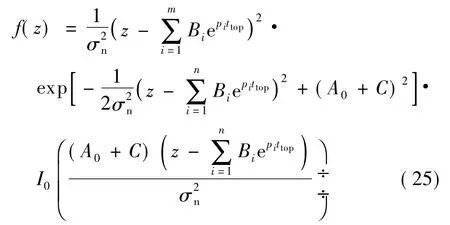
由样本集估计所得PDF的仿真值进行回归拟合分析，修正为

由图3(b)可见，修正后的PDF与Matlab仿真值相差甚微.

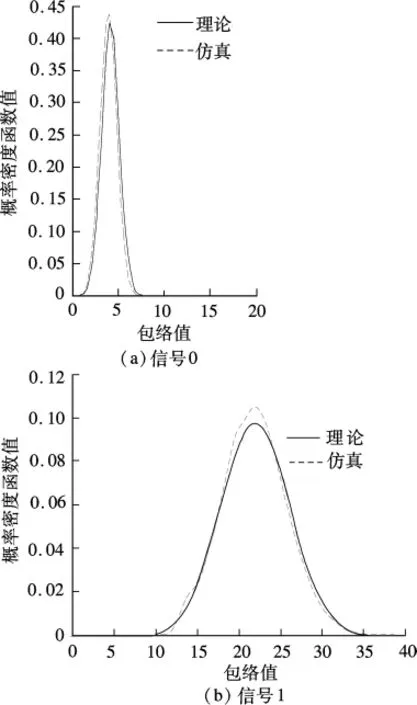
图3 冲击滤波后含噪EBPSK信号概率密度函数值

2.2 积分判决

针对EBPSK信号冲击滤波输出的波形特点，对冲击最高的区间内一小段信号波形进行积分，可避免冲击最大值不一定在同一时刻达到的缺点.

对由接收信号r0(t)进行小区间内积分

式中，tmin，tmax分别为取积分的左边界和右边界.对其进行简化估计得则其PDF服从改进后的广义瑞利分布

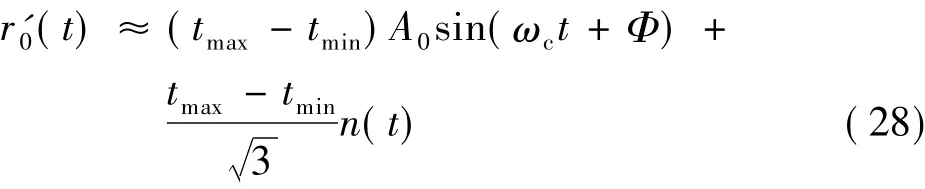
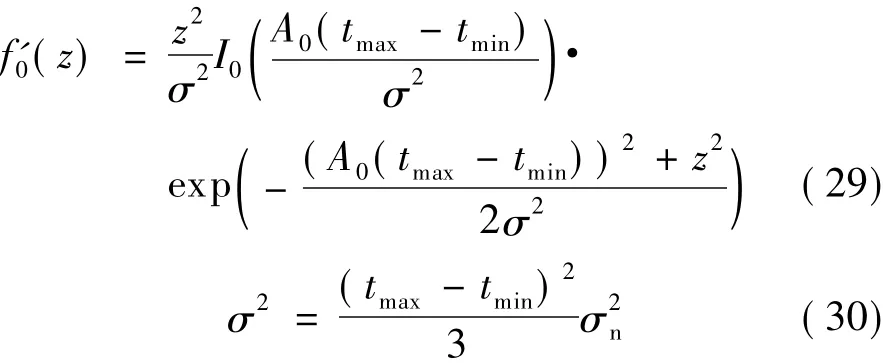
图4给出了该PDF的理论分析值与Matlab仿真值的比较.

对接收信号r1(t)进行小区间积分

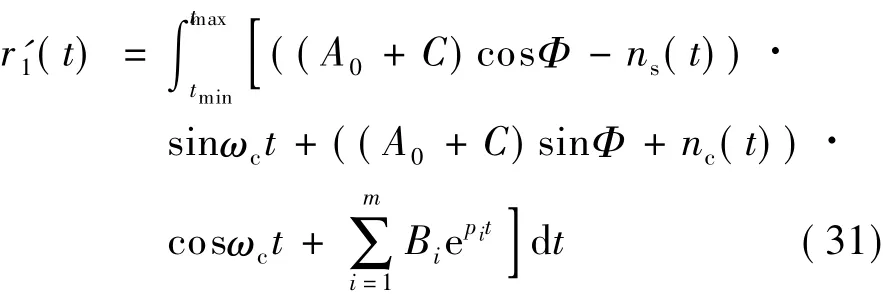
将检测量简化为

可见其检测量服从改进的广义瑞利分布

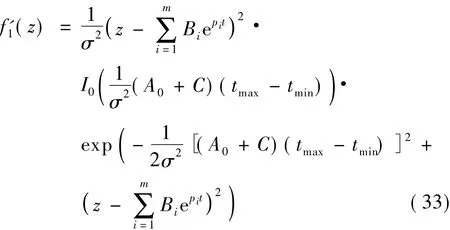
根据冲击滤波器的输出波形特征，选取tmax=ttop+T/100，同理tmin=ttop－T/100.其PDF的理论曲线与仿真曲线如图4所示.

若发送比特0和1等概率，则判决门限的值b由 f′1(b)=f′0(b) 求得.

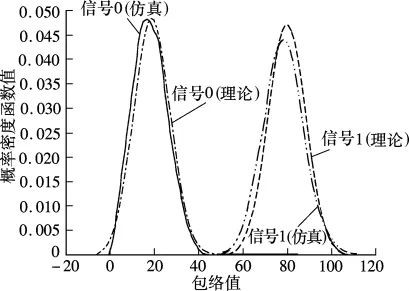
图4 积分判决下信号0与1的理论和仿真PDF比较

3 误比特率性能分析

3.1 采用抽样判决

假设发送信号0和1等概率，发送0时错判为1的概率为

发送1时错判为0的概率为

则系统总的误比特率公式为

Marcum Q函数定义为

3.2 采用积分判决

假设发送信号0和1等概率，发送0时错判为1的概率为

发送1时错判为0的概率为

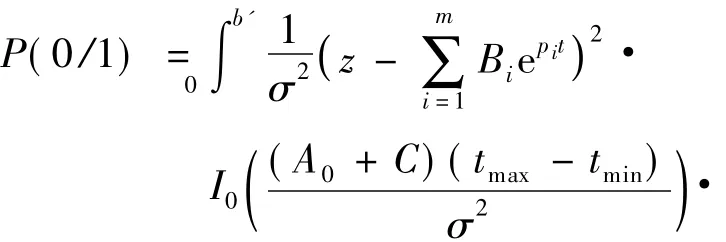
则系统的总误比特率为

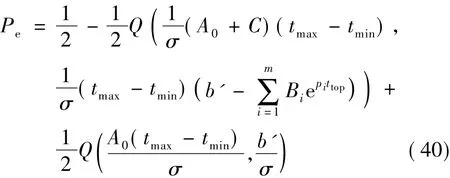
式中，b′为积分判决的判决门限.

由式(36)和(40)得到的BER理论值与仿真值对比如图5所示，显见积分判决的抗噪声性能比抽样判决提升了1 dB，而且随着信噪比的增大，积分判决的误比特率下降更快，表明了积分判决更适合EBPSK解调，具有重要的理论指导意义.

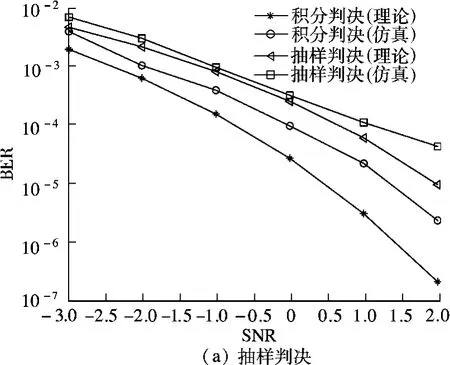
图5 积分判决、抽样判决理论与仿真误码率比较

4 结语

从概率统计与回归拟合的角度对冲击滤波器输出估计出经过经典抽样判决检测和积分判决检测的PDF，论证了AWGN信道EBPSK的最佳解调性能.在BER角度上，冲击滤波解调和积分判决成为EBPSK调制信号的最佳接收结构，且对此只有冲击滤波器的暂态响应部分能够提高解调性能.

冲击滤波器是决定EBPSK解调性能的关键因素，将不同的滤波器系数按照本文方法得到抽样判决与积分判决的BER表达式后，即可评估该滤波器用于EBPSK解调时的性能上界.

References)

［1］吴乐南.超窄带高速通信进展［J］.自然科学进展，2007，17(11):1467-1473.Wu Lenan.Progress in ultra narrow band communication［J］.Progress in Natural Science，2007，17(11):1467-1473.(in Chinese)

［2］何善宝，林益明，吴乐南.星间链路新型信号体制设计［J］.中国空间科学技术，2011(4):15-22.He Shanbao，Lin Yiming，Wu Lenan，et al.Design of new signal system for inter-satellite links［J］.Chinese Space Science and Technology，2011(4):15-22.(in Chinese)

［3］冯熳，高鹏，吴乐南.超窄带调制信号的特殊滤波分析与仿真［J］.东南大学学报:自然科学版，2010，40(2):227-230.Feng Man，Gao Peng，Wu Lenan.Analysis and simulation of special filtering based on ultra narrow band modulated signal［J］.Journal of Southeast University:Natural Science Edition，2010，40(2):227-230.(in Chinese)

［4］马力，冯熳，吴乐南.EBPSK数字接收滤波器设计［J］.科技创新导报，2008(28):28-29.Ma Li，Feng Man，Wu Lenan.Design of digital filter in EBPSK receiver［J］.Science and Technology Innovation Herald，2008(28):28-29.(in Chinese)

［5］ Wu Lenan，Feng Man.On BER performance of EBPSK-MODEM in AWGN channel［J］.Sensors，2010，10(4):3824-3834.

［6］ Feng Man，Wu Lenan，Ding Jiajia，et al.BER analysis and verification of EBPSK system in AWGN channel［J］.IEICE Communication Letter，2012.(to appear)

［7］卢宁.超窄带接收机滤波模型与优化设计［D］.南京:东南大学信息科学与工程学院，2010.

［8］ Walker H R.Digital modulation device in a system and method of using the same:USA，6445737［P］.2002.

［9］ Bobier J A.Missing cycle based carrier modulation:USA，6968014B1［P］.2005.

［10］戚晨皓，陈国强，吴乐南.二阶锁相环的EBPSK信号解调分析［J］.电子与信息学报，2009，31(2):418-421.Qi Chenhao，Chen Guoqiang，Wu Lenan.EBPSK demodulation analysis based on second-orderphase locked loop［J］.Journal of Electronics＆Information Technology，2009，31(2):418-421.(in Chinese)

［11］ Proakis J G.Digital communication［M］.4th ed.New York:McGraw-Hill，2002:169-176.