变速恒频双馈风力发电机并网的复合控制

周明明 李世华

(东南大学自动化学院，南京 210096)(东南大学复杂工程系统测量与控制教育部重点实验室，南京 210096)

在双馈风力发电系统中，发电机与网侧是柔性连接关系，可通过调节转子励磁电流实现软并网，避免并网时发生的电流冲击和过大的电压波动.变速恒频风力发电机的并网方式主要有空载并网、带独立负载并网和孤岛并网［1］.对于空载并网方式而言，并网前发电机不带负载，不参与能量和转速的控制，实现简单.

文献［2-4］介绍了双馈电机空载并网PI控制，将矢量变换技术移植到发电机并网控制上，提出了一种基于定子磁链定向方式的空载并网控制方法，但这种控制方法对电机参数的依赖性较高，实时性和抗扰动性能都较差.文献［5］介绍了一种基于自抗扰控制的并网策略，该控制策略不需要精确电机参数就可以实现并网控制，并对参数的摄动以及内外扰动都具有良好的鲁棒性.

滑模控制是一种有效的非线性控制方法，文献［6-7］介绍了双馈电机空载并网积分滑模控制，其效果不仅在于动态响应速度快，而且系统进入滑动模态后对参数摄动和外部扰动具有强鲁棒性.

上述滑模控制方法中系统状态到滑模面后都是在无限时间后才能到达平衡点，为此，文献［8］提出一种新的终端滑模控制设计方法，即在滑动超平面的设计中引入非线性函数，构造终端滑模面，使得在滑模面上系统状态能够在有限时间内收敛到零.与传统的滑模控制方法相比，该方法具有更好的收敛性.终端滑模控制已被应用于许多不同的领域，并取得了良好的效果，如机械臂系统［9-10］、空间飞行器［11］及永磁同步电机转子位置的观测［12］.

无论是传统的滑模控制还是终端滑模控制，如何削弱抖振都是一个重要的问题.针对滑模控制固有的抖振现象，常用的抖振削弱方法是采用饱和函数或S型函数代替开关函数，这实际上是一种近似化处理，会降低系统的抗扰动性能.引入扰动观测前馈补偿策略，估计出扰动并进行补偿，这样系统的滑模控制律可以选取更小的切换增益值，达到既不牺牲抗扰动性能又可以削弱抖振的目的.

风电并网控制系统在并网之前需要使得风力发电机的定子电压跟踪上电网电压，以实现风力发电机平滑地接入电网.本文针对风电并网控制系统的特点，利用终端滑模控制方法，设计了一种新型的并网控制策略，同时采用扩张状态观测器观测出系统的扰动并进行前馈补偿，有利于减小终端滑模控制中切换控制增益的取值和削弱抖振.由于设计的终端控制律中不存在状态变量的负分数幂，避免了传统终端滑模控制的奇异性问题.仿真结果表明，该复合控制算法能够顺利实现并网并且动态响应快、超调更小.

1 双馈发电机并网矢量控制

在不计铁心饱和、忽略谐波磁势影响、气隙均匀的情况下，双馈发电机在同步速旋转坐标系下的数学模型为［4］:

1)电压方程

2)磁链方程

3)电磁转矩方程和运动方程

式中，Rs，Rr分别为定、转子绕组等效电阻；Ls，Lr，Lm分别为 d，q轴定、转子绕组自感及互感；id，s，iq，s，id，r，iq，r分别为 d，q 轴定、转子电流；ud，s，uq，s，ud，r，uq，r分别为 d，q 轴定、转子电压；ψd，s，ψq，s，ψd，r，ψq，r分别为 d，q 轴定、转子磁链；ω1，ωr，ωs分别为同步角速度、转子角速度和转差角速度；Tm为机械转矩；Te为电磁转矩；J为转动惯量；np为电机极对数；p为微分算子.

为了避免并网时的电流冲击和转轴受到突然的扭矩，需要满足一定的并网条件，即双馈风力发电机定子电压的幅值、频率、相位和电网电压的一致.发电机并网控制就是在并网之前调节定子电压，满足并网条件后进行并网操作.由于并网前，双馈发电机空载运行，定子线圈中没有电流，即id，s=iq，s=0，于是可推得

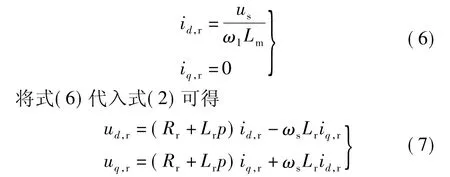
由式(7)所表示的转子电压方程可以设计出并网矢量控制系统，如图1所示.由式(6)可知，d轴电流的给定信号与电机参数Lm有关，而当Lm参数不精确时，会引起定子电压幅值偏差，降低并网成功率.本文采用定子电压外环串级控制系统，电网电压幅值与定子电压幅值的差值经PI控制器调节后得到转子d轴电流参考值，而不再需要精确互感参数Lm，保证定子电压幅值满足并网条件.同时考虑到实际动态过程中磁场定向的误差，iq，r一般不为零，于是对iq，r也进行闭环调节.

图1 双馈发电机并网控制系统框图

并网控制过程中，根据检测的电网电压信息对转子电流进行闭环控制，发电机转子电流控制得好坏，决定了定子电压的性能.常规PI控制方法设计的转子电流控制器对电机参数的依赖性较高，转子绕组的参数扰动会影响机组并网，降低并网的成功率.

2 复合终端滑模控制器设计

由式(7)可知，转子电流微分方程为

考虑双馈电机转子绕组参数扰动，式(8)表示为

式中，Δfd，Δfq为相应的转子绕组参数变化引起的扰动.由于在系统中可以得到 ωsiq，r和 ωsid，r的精确值，整理式(9)可得

式中，wd和wq可视为系统的广义扰动，分别表示为

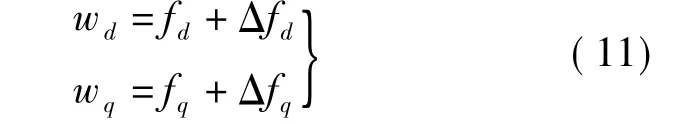
2.1 转子电流终端滑模控制器设计

由式(10)可以看出，d轴电流的微分方程与q轴电流的微分方程相似，本文以d轴电流控制器设计为例说明转子电流控制器设计的过程.d轴电流控制器用于精确跟踪d轴电流参考信号，定义d轴电流误差状态为ed=－ id，r，则 d 轴电流误差系统方程为

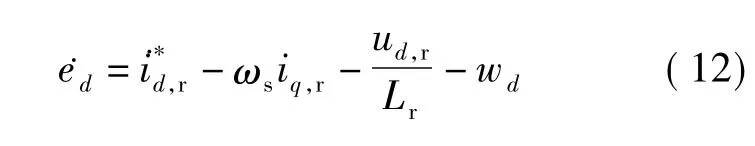
为了提高转子电流的响应速度和跟踪精度，本文提出如下终端滑模面:

式中，c1＞0，p1，q1均为奇数，且0 ＜p1/q1＜1.

根据终端滑模的有限时间收敛机制，通过设计适当的滑模控制律使得sd在有限时间内收敛到零后，在滑模面上误差ed也会在有限时间内收敛到零.与一般滑模控制的分析类似［13］，此处需要假设系统的扰动是有界的.

假设1 系统扰动wd是有界的，满足≤ld.

于是，得到如下定理.

定理1 若风电并网控制系统满足假设1，选取如式(13)的终端滑模面，当切换增益k1＞Lrld时，有如下控制律:

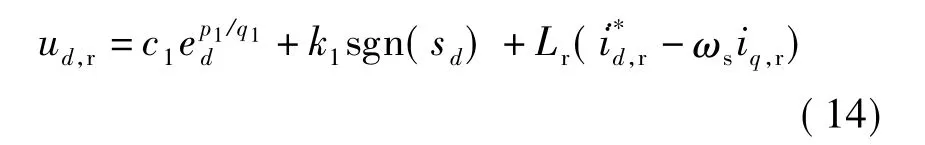
可以使得发电机转子d轴电流误差ed在有限时间内收敛到零.

证明 选取李雅普诺夫函数为Vd=0.5s2d，则其对时间求导得

根据上述分析，可以验证Vd将在有限时间内收敛到零，即转子d轴电流误差将在有限时间内到达滑动面sd=0，并保持在滑动面上.

设sd(0)≠0到sd(t)=0的时间为tr，当sd=0时，有e˙d+=0，即=－两端进行积分后有

则由sd(0)≠0到ed(ts)=0的总时间计算式为

2.2 基于ESO的抖振削弱方法

扩张状态观测器(ESO)是一种性能良好的观测器，它不仅能得到不确定对象的状态，还能获得对象模型中内扰(不确定项)和外扰总的实时控制量，把该控制量补偿到控制系统中，就可以抑制扰动，进而改善系统的性能.

由于式(10)d轴电流微分方程中的ωsiq，r项可以通过计算得到精确值，所以设计的ESO只需要观测扰动wd的值，这样可以减轻ESO对扰动估计的负担，提高对扰动估计的精度.标准的ESO采用的是非线性的观测器形式，需要调节的参数较多.此处，为了实现的简便性，采用文献［14］的线性观测器形式.

由此，d轴电流控制器的ESO可设计成如下形式:

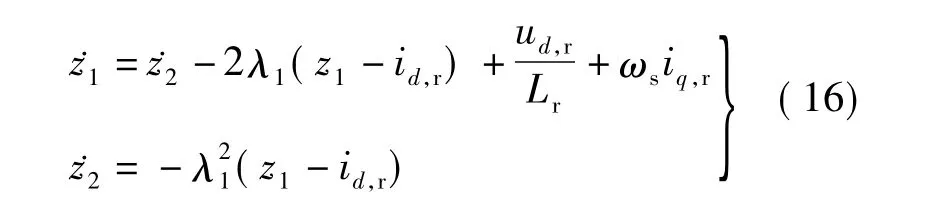
式中，z1估计的是双馈发电机的转子电流id，r；z2估计的是系统的广义扰动wd；－λ1(λ1＞0)为 ESO的闭环期望极点.选取终端滑模面如式(13)所示，此时d轴转子电流控制中ud，r可设计为

式中，－Lrz2为控制律的前馈补偿部分.图2为复合终端滑模转子电流控制器原理框图.

假设2 wd是系统的广义扰动，z2是通过ESO对wd的估计值，假设 wd－z2是有界的，满足≤l'd.

定理2 若风电并网系统满足假设2，采用式(17)的控制律，当切换增益k'1＞Lrl'd时，则发电机转子d轴电流误差ed在有限时间内收敛到零.

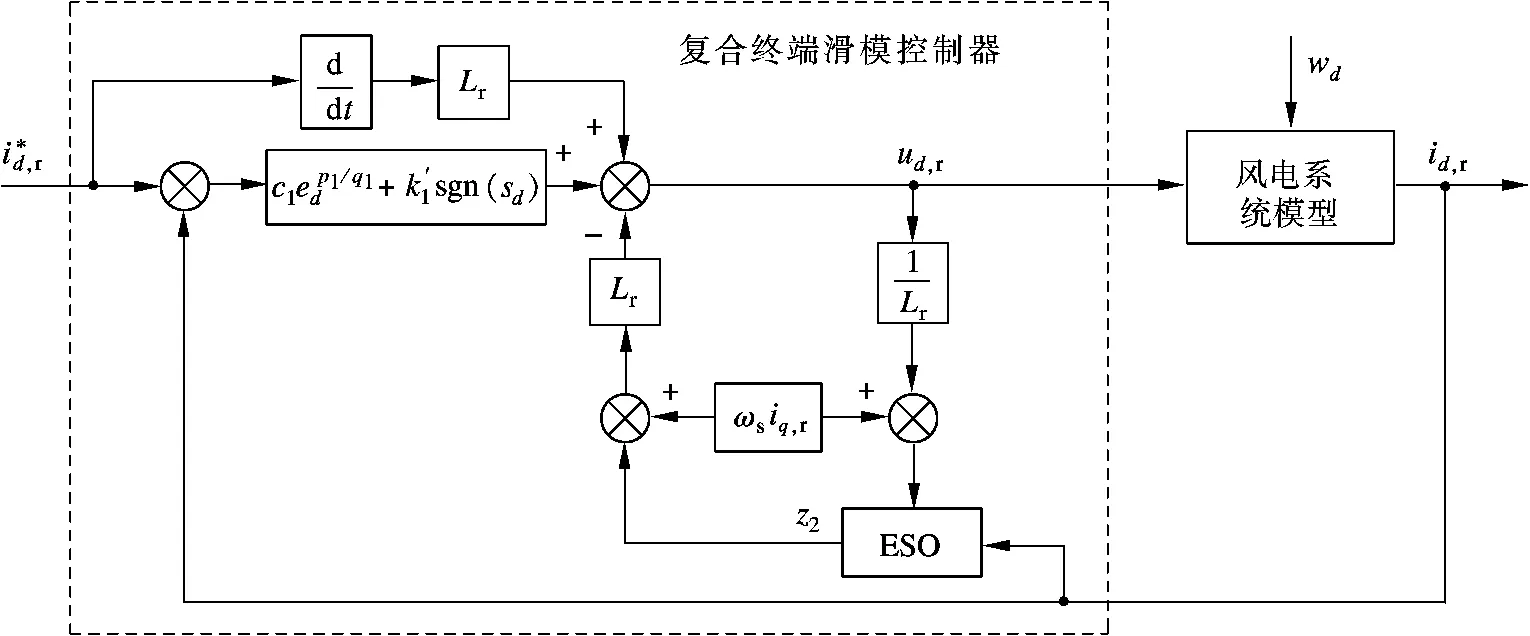
图2 基于ESO的复合终端滑模转子电流控制器原理框图

证明 参考定理1的证明过程，选取李雅普诺夫函数为Vd=0.5s2d，则其对时间求导得

显然满足滑模到达条件˙Vd＜0.由于选取了相同的终端滑模面函数，当电流误差ed达到滑模面后，也能在有限时间内收敛到零.

定理2的结论与定理1类似，不同的是定理2所示的控制律中引入了一个前馈补偿项.2种设计得到的滑模面方程为(后者为复合终端滑模控制情况)

从上面比较可以看出，当ESO选择合适的控制器参数后，z2能够很好地估计出扰动wd，此时系统总扰动为wd－z2，其上界值l'd一般会比wd的上界ld要小得多.因此，在不牺牲系统抗扰动性能的前提下，与仅用终端滑模控制的情况相比，基于ESO的复合终端滑模控制器的切换增益k'1能够选取得更小，系统抖振情况会大大削弱.

3 系统仿真分析

本文在Matlab/Simulink平台上搭建了变速恒频双馈风力发电系统空载并网仿真模型，所用双馈发电机参数［5］(折算到定子侧):额定功率为21 kW，额定电压380 V，额定频率50 Hz，定子电阻Rs=0.6 Ω，定子自感 Ls=157 mH，转子电阻 Rr=0.8 Ω，转子自感 Lr=157 mH，互感 Lm=153 mH，转动惯量J=0.189 kg·m2，极对数np=2；电网参数为380 V和50 Hz.为模拟变速发电过程，给发电机施加20 N·m的拖动力矩.

分别采用常规PI控制、终端滑模控制(TSM)和复合终端滑模控制(TSM+ESO)的并网控制策略进行仿真.控制器参数分别为:PI控制中d轴电流控制器kp=50，ki=16.5，q轴电流控制器kp=20，ki=1500；TSM 控制中d轴电流控制器 c1=50，p1=3，q2=5，k1=5，q 轴电流控制器 c2=5，p2=3，q2=5，k2=16；TSM+ESO 控制中d轴电流控制器k'1=0.5，λ1=2000，q轴电流控制器k'2=2，λ2=2000，其他参数与TSM 控制中的相同.

图3为理想情况下，并网前双馈发电机在不同转速下转子d，q轴电流，定子A相电压和电网A相电压的动态响应波形比较.从图中可见，在终端滑模控制中，响应速度很快，但为了抑制扰动的影响，切换增益取值较大，使得转子电流，尤其是q轴电流抖振较大(图3(c)是(b)放大后的情况，对比较明显)，定子电压波形不平滑；在复合终端滑模控制中，d轴电流的动态响应与终端滑模控制的差不多，q轴电流控制器中虽然切换增益取值较小，但由于有扰动前馈补偿作用，能使得转子q轴电流保持在零值，且抖振比终端滑模控制的情况小得多，有更平滑些的定子电压波形.常规PI控制响应速度相对较慢，要提高响应速度，就会产生很大的超调，还会影响到系统的稳定性.

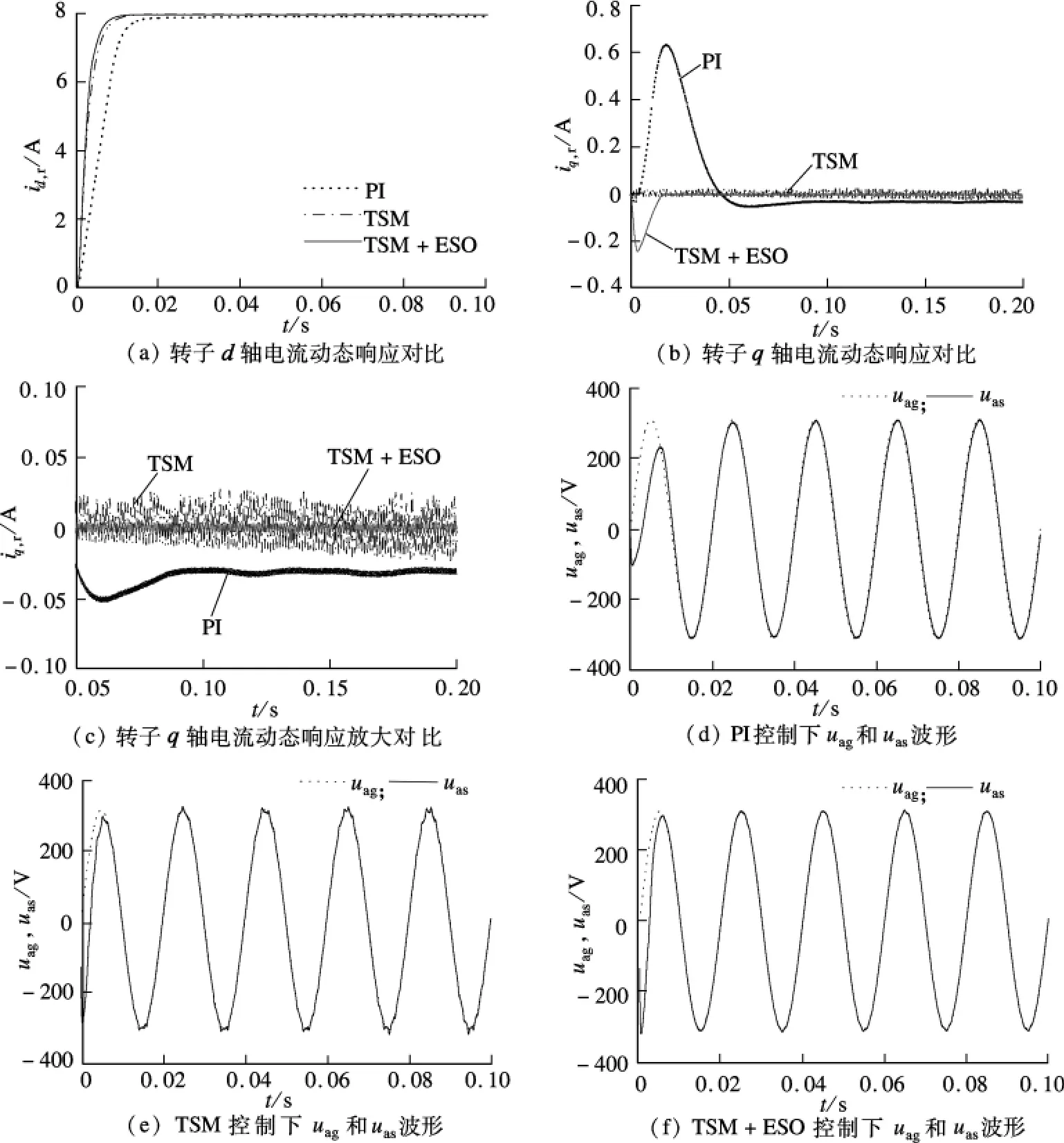
图3 不同转速下PI，TSM和TSM+ESO控制的动态响应

图4 PI与TSM+ESO控制对参数摄动时的动态响应

由于电机运行时，电阻会随着温度的升高而增大，电感会随着磁路的饱和而减小，假设双馈发电机转子电阻参数增大50%，电感参数减小2%，系统空载运行结果如图4所示.常规PI控制下的系统空载并网动态响应性能变差，稳态误差也变大；复合终端滑模控制下的系统空载并网动态响应曲线基本没有变化，仍旧保持良好的动态性能和稳态性能，对电机参数摄动具有较强的鲁棒性.

图5为该复合控制策略在1.5 s并网后的定子A相电流波形，在并网时定子电流很小，不会产生冲击电流.

4 结语

本文针对变速恒频风力发电并网系统，提出了一种基于终端滑模和扩张状态观测器的复合控制算法，使得闭环系统不仅具有更快的响应，而且在保证强的抗扰动性能情况下具有更小的抖振，对该并网控制策略给出了稳定性分析.仿真研究表明，该复合控制策略有效可行，具有良好的动态性能和控制精度，可迅速地控制发电机定子电压满足并网条件，有效地抑制了发电机并网时的冲击电流，具有良好的鲁棒性.

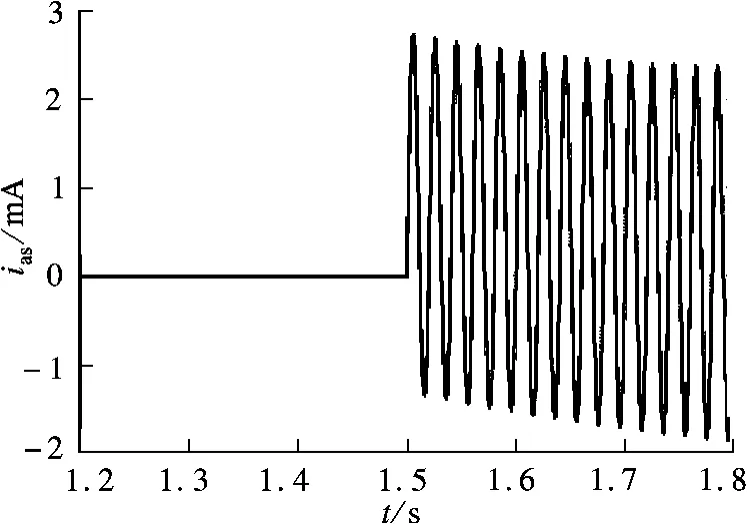
图5 并网时的定子A相电流波形

References)

［1］李建林，赵栋利，李亚西，等.几种适合变速恒频风力发电机并网方式对比分析［J］.电力建设，2006，27(5):8-10，17.Li Jianlin，Zhao Dongli，Li Yaxi，et al.Comparison and analysis on network synchronization modes of several kinds of VSCF wind power generator［J］.Electric Power Construction，2006，27(5):8-10，17(in Chinese).

［2］刘其辉，贺益康，卞松江.变速恒频风力发电机空载并网控制［J］.中国电机工程学报，2004，24(3):6-11.Liu Qihui，He Yikang，Bian Songjiang.Study on the no-load cutting-in control of the VSCF wind-power generator［J］.Proceedings of the CSEE，2004，24(3):6-11.(in Chinese)

［3］刘其辉，贺益康，张建华.交流励磁变速恒频风力发电机并网控制策略［J］.电力系统自动化，2006，30(3):51-55，70.Liu Qihui，He Yikang，Zhang Jianhua.Grid connection control strategy of AC-excited VSCF wind power generator［J］.Automation of Electric Power Systems，2006，30(3):51-55，70.(in Chinese).

［4］赵栋利，许洪华，赵斌，等.变速恒频风力双馈发电机并网电压控制研究［J］.太阳能学报，2004，25(5):587-591.Zhao Dongli，Xu Honghua，Zhao Bin，et al.Study on the cut-in voltage control of a VSCF double-fed induction generator［J］.Acta Energiae Solaris Sinica，2004，25(5):587-591.(in Chinese).

［5］付旺保，赵栋利，潘磊，等.基于自抗扰控制器的变速恒频风力发电并网控制［J］.中国电机工程学报，2006，26(3):13-18.Fu Wangbao，Zhao Dongli，Pan Lei，et al.Cutting-in control of the VSCF wind-power generator based on auto-disturbance rejection controller［J］.Proceedings of the CSEE，2006，26(3):13-18.(in Chinese).

［6］侯勇，童建东.变速恒频双馈风力发电机并网积分型变结构控制［J］.电机与控制学报，2008，12(3):260-265.Hou Yong，Tong Jiandong.Cutting-in control of VSCF double-fed wind-power generator with integral variable structure control［J］.Electric Machines and Control，2008，12(3):260-265.(in Chinese).

［7］夏长亮，王慧敏，宋站锋，等.变速恒频双馈风力发电系统空载并网积分变结构控制［J］.天津大学学报，2008，41(11):1281-1286.Xia Changliang，Wang Huimin，Song Zhanfeng，et al.Integral variable structure controller for no-load cuttingin control of VSCF wind-power system with doubly-fed induction generator［J］.Journal of Tianjin University，2008，41(11):1281-1286.(in Chinese).

［8］Man Zhihong，Paplinski A P，Wu H R.Robust MIMO terminal sliding mode control scheme for rigid robotic manipulators［J］.IEEE Transactions on Automatic Control，1994，39(12):2464-2469.

［9］Feng Yong，Yu Xinghuo，Man Zhihong.Non-singular terminal sliding mode control of rigid manipulators［J］.Automatica，2002，38(12):2159-2167.

［10］Yu Shuanghe，Yu Xinghuo，Man Zhihong.Continuous finite-time control for robotic manipulators with terminal sliding mode［J］.Automatica，2005，41(11):1957-1964.

［11］Ding Shihong，Li Shihua.Stabilization of the attitude of a rigid spacecraft with external disturbances using finite-time control techniques［J］.Aerospace Science and Technology，2009，13(4/5):256-265.

［12］Feng Yong，Zheng Jianfei，Yu Xinghuo，et al.Hybrid terminal sliding-mode observer design method for a permanent-magnet synchronous motor control system［J］.IEEE Transactions on Industrial Electronics，2009，56(9):3424-3431.

［13］Khalil Hassan K.Nonlinear systems［M］.3rd ed.London:Prentice Hall，2002.

［14］Li Shihua，Liu Zhigang.Adaptive speed control for permanent-magnet synchronous motor system with variations of load inertia［J］.IEEE Transactions on Industrial Electronics，2009，56(8):3050-3059.