被动型氢原子钟储存泡口原子分布计算及应用
王勇 李建清 邱实
(东南大学仪器科学与工程学院,南京 210096)
被动型氢原子钟是以氢原子超精细结构能级之间的跃迁产生的频率准确性和稳定性极高的微波波谱信号作为参考的频率和时间计量装置[1-2],其体积、重量相对较小,但相对于其他小型原子钟具有无可比拟的中、长期稳定度,所以被广泛用于卫星导航、空间探测和通信等系统,为其提供标准时间、频率源[3].磁选态器是制备产生有效跃迁信号的高能态氢原子和产生微波信号的基础.常用的磁选态器有六极磁选态器和四极磁选态器[4-5].其中,四极磁选态器比六极磁选态器要短小[5],更适用于星载小型氢原子钟,它可使束光学系统缩短,提高效率,减小真空泵负担,延长氢原子钟的寿命.文献[5-7]都给出了四极磁选态器的计算、设计过程以及氢原子在系统中的运动,但是都仅计算了特定条件下原子的运动轨迹和截获角,而没有考虑原子从准直孔出射的角度和速度复杂的分布情况.本文在给出氢原子在四极磁选态器中运动原理的基础上,结合原子出射角度和出射速度的分布概率,计算得到原子在储存泡口的分布规律,建立更贴近实际情况的模型.并应用改进的泡口分布模型优化泡口直径和聚焦距离,使得高能态原子被最大程度聚集,而低能态原子被偏离,为被动型氢原子钟储存泡口的直径和聚焦距离的设计提供了依据,有利于提高跃迁信号的功率.
1 氢原子在四极磁选态器中的偏转
基态氢原子在微弱磁场(磁场强度为H)中具有4个超精细结构能级,其能量可表示为[1]

式中,F=1时,mF=0,±1,取“+”,F=0 时,mF=0,取“-”;h为普朗克常数;υ为跃迁信号的频率;μB为玻尔磁子;对于基态氢原子gJ=2.002284,gI=0.003042,x=H.由式(1)得到各个能态氢原子能量随外磁场强度变化的关系,如图1所示.

图1 氢原子基态超精细分裂能级图
如图2所示的四极磁选态器由4个磁极组成,当沿磁铁长度方向上磁势是均匀的,且每个磁极占据60°时,其磁势 V 和磁场强度 H 分别为[1,5]
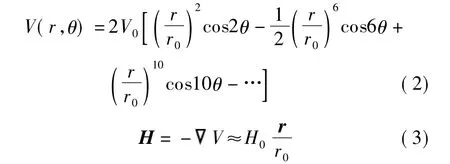
式中,H0为磁极顶点的磁场强度;r0为磁极半径.由式(3)可知,四极磁选态器的磁场强度与场点的半径r成正比,且磁场梯度大小约为常数[5],即H≈H0/r0.
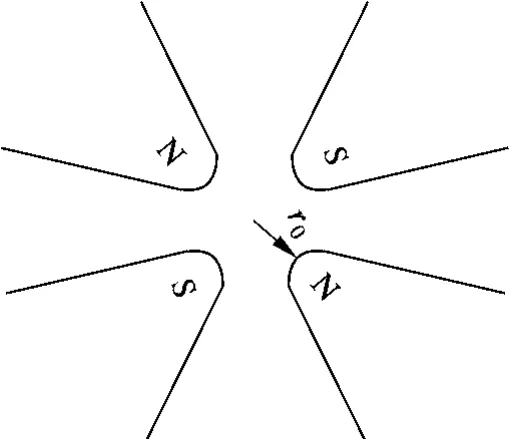
图2 四极磁选态器示意图
氢原子核自旋和电子自旋的耦合使氢原子具有磁矩,在磁场中氢原子的有效磁矩μeff和受到磁场的作用力Fm为[6-8]

式中,Em为氢原子在磁场中的附加能量.在磁场中,=1,mF=0〉和=1,mF=1〉两态氢原子μeff<0,故称为负磁矩态氢原子,受到向心力;=1,mF=-1〉和=0,mF=0〉两态氢原子 μeff>0,故称为正磁矩态氢原子,受到散射力[6],产生了如图3所示的负磁矩态氢原子被聚焦和正磁矩态氢原子被散射的不同运动轨迹.
设氢原子从四极磁选态器前面中心轴上距离磁选态器l1的准直孔中泻流出来,初速为v0,并与中心轴有一小角度δ0,根据牛顿运动定律,氢原子在四极选态磁场中的运动方程为[1,6]
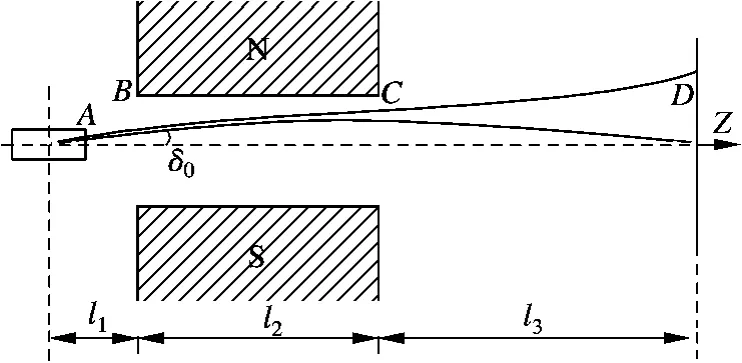
图3 氢原子在四极磁选态器中的运动轨迹图

式中,m为氢原子的质量;r为氢原子的横向(垂直于图3中 Z轴方向)位移;负磁矩态氢原子取“+”,正磁矩态氢原子取“-”,且原子在四极选态磁场内部运动的初始条件为

所以,氢原子在四极选态磁场中的横向速度和位移可表示为

式中,负磁矩态氢原子取“-”,正磁矩态氢原子取“+”.在四极选态磁场出口C处横向速度和位移为[6]
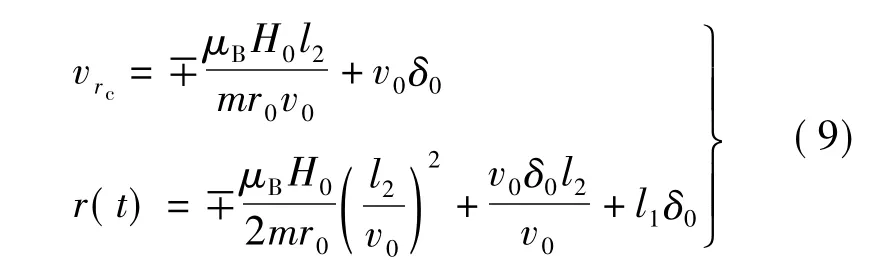
式中,l2为四极磁选态器长度.各个能态氢原子经过聚焦距离l3到达储存泡口所在的D处,在D处产生有效微波信号(1.420405751768 GHz)跃迁的高能态和相应的低能态氢原子的横向位移分别为

令式(8)中 vr(t)=0,r(t)=r0,且取“-”,可得高能态氢原子最大截获角为[1,6]
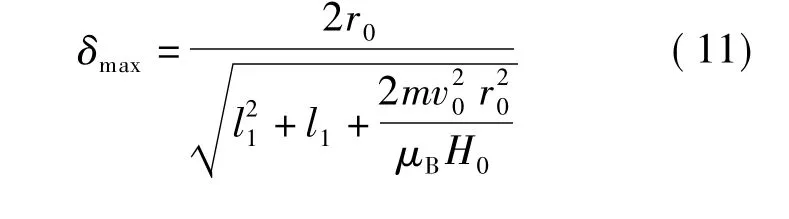
将系统的设计参数l1=9 mm,r0=1.2 mm,H0=0.9 T代入式(10),并且v0取T=300 K时的最可几速率,可得 δmax≈3°.
2 氢原子在储存泡口分布规律计算
以上计算了在一定出射速度v0和出射角δ0下产生有效微波信号跃迁的高能态和低能态氢原子在四极磁选态器中的偏转.但是,在一定温度下氢原子的出射速度v服从麦克斯韦速度分布[9]
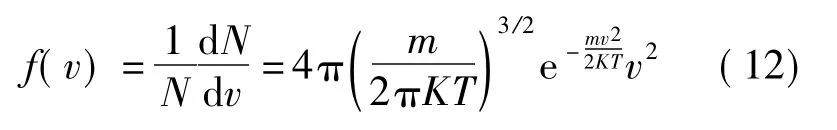
式中,K为玻尔兹曼常数;T为氢原子的温度.该分布如图4所示,且在最可几速率vp=处概率最大.

图4 氢原子的麦克斯韦分布(T=300 K)
除了氢原子出射速率服从麦克斯韦分布以外,文献[5]还给出了氢原子从不同的深径比L/a(L为准直孔深度,a为准直孔直径)准直孔泻流的出射角分布,如图5所示.可以看出,在深径比足够大(L/a>20)情况下氢原子从准直孔中泻流的出射角分布近似为均匀分布,所以本文将到达储存泡口平面D处的氢原子的出射速度近似处理为服从(0,δmax]均匀分布,计算中取 δmax=3°.

图5 出射角度分布[5]
氢原子出射速度服从麦克斯韦分布,出射角度服从均匀分布,将2个分布代入式(10),高能态和低能态氢原子在储存泡口D的横向位移rDH和rDL的分布规律将会变得较为复杂.本文采用一种数值计算方法得到其分布规律,计算过程如下.
1)研究出射原子的速度分布对原子在储存泡口分布概率的影响.将一定数目的氢原子按照速度的麦克斯韦分布进行分配,根据相应的速度分别计算式(10)中的横向位移以及相对应的速度[v,v+dv]的分布概率,由此得到一定出射角度下横向位移取值的分布规律.图6是氢原子在出射角为δ→0°和δ=3°时高能态和低能态氢原子横向位移取值分布.
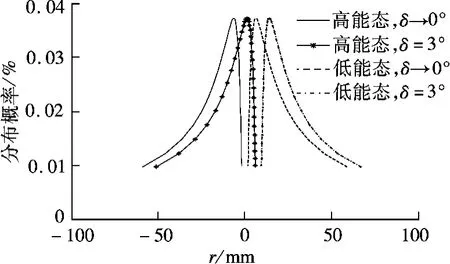
图6 一定出射角度下横向位移分布
2)研究出射原子的出射角度分布对原子在储存泡口分布概率的影响.因为出射角度服从(0°,3°]均匀分布,所以将一定数量的高能态或低能态氢原子按0.03°出射角步距分配成100份,每一份原子再按上述速度的麦克斯韦分布进行分配,并按步骤1)的计算过程得到每一个出射角度下横向位移取值的分布规律,并将均匀分布的各个出射角度下的分布概率进行叠加处理,最终得到高能态和低能态氢原子在泡口D处横向位移取值的总体分布规律,如图7所示.由式(2)和(3)可知,四极磁选态器中的磁场具有横向对称性,故高、低能态氢原子在每个纵向(平行于Z轴方向)截面上的运动轨迹和分布规律具有一致性.因此,可以由图7所示的一维分布规律旋转得到在储存泡口D平面内高能态和低能态氢原子的三维分布规律,图8为D平面内高能态和低能态氢原子的三维分布规律.图中,rx和ry分别为D平面内2个垂直方向上的横向位移.
由以上的计算与分析可得到如下结论:
1)高能态氢原子聚焦于储存泡口中心位置附近,且中心处分布概率最高,而低能态氢原子分布在高能态氢原子外围,且有部分叠加.
2) 在系统设计参数 H0,l1,l2,r0确定的情况下,聚焦距离l3越小,高能态和低能态原子的分布越向中心位置靠近,且分布概率模型的方差越小.
3)在中心轴处一个很小的范围内(见图7中rc),低能态原子分布概率为0,高能态原子概率最大.

图7 高、低能态氢原子D处横向位移总体分布
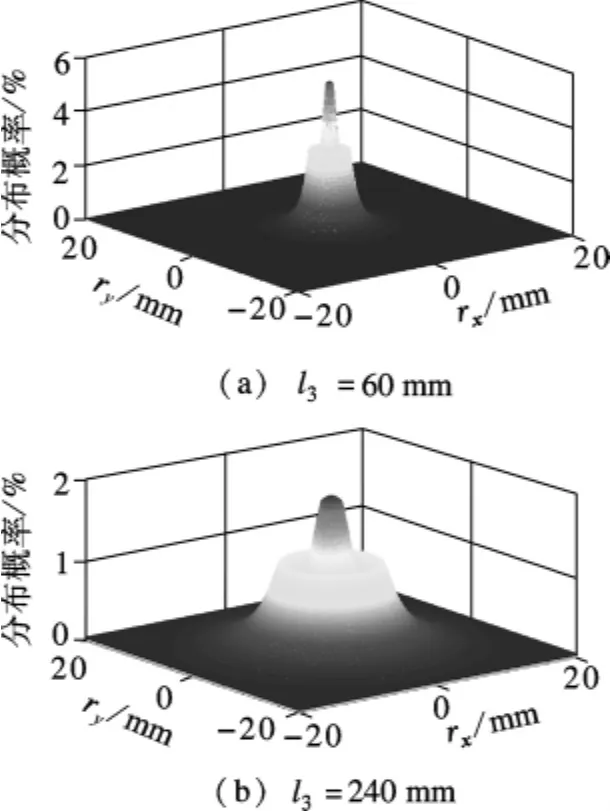
图8 高、低能态氢原子D平面内三维分布
3 聚焦距离和储存泡口直径的优化
储存泡是被动型氢原子钟的重要部件,它收集高能态氢原子,并使其较长时间停留在谐振腔内,与辐射场相互作用,有利于增加原子受激辐射的能量,提高谐振腔内跃迁信号强度[10].
聚焦距离l3和储存泡口的直径是系统设计的2个重要参数,其设计的原则是使更多产生有效信号跃迁所需要的高能态原子聚焦,而通过储存泡口进入泡内,使低能态氢原子尽量不进入储存泡而被真空系统抽走,从而优化系统性能,提高信号谱线的功率,优化弛豫时间.本节从统计学的观点出发,应用上一节计算得到的高、低能态氢原子经过四极磁选态器偏转后在泡口的数学分布模型来优化聚焦距离和泡口直径这2个参数.
由第2节中的结论3)可知,在半径rc范围内低能态氢原子分布概率为0,高能态氢原子分布概率最高,高、低能态原子分布无叠加,将高能态原子聚焦在半径rc以内,则高能态原子的利用率最高,而低能态原子不进入泡内,可使系统性能得到优化,故将此半径rc定义为泡口的优化半径.由第2节中的结论2)可知,泡口的优化半径随着聚焦距离的增大而增大.利用数值计算的方法,计算l3不同取值下的rc,可以得到图9所示聚焦距离和泡口优化半径之间的数量关系.
按图9所示的聚焦距离和储存泡口优化半径之间的数量关系曲线设计系统的聚焦距离和泡口直径,可使被动型氢原子钟的束光系统的性能得到优化,提高了储存泡对高能态氢原子的收集效率.
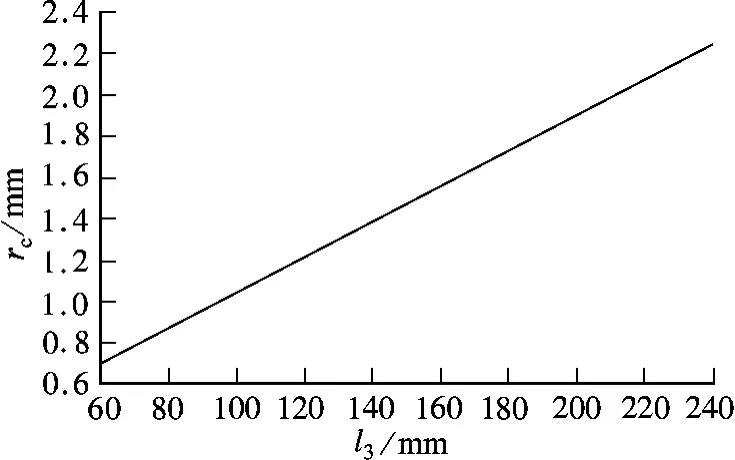
图9 聚焦距离和储存泡口优化半径的数量关系曲线
4 结论
1)经过四极磁选态器的偏转,高、低能态氢原子的横向偏移r的分布不仅和磁选态系统的设计参数有关,还和出射速度v和出射角δ的分布有关.
2)在一定温度且最大截获角δmax很小(小于5°)的情况下,氢原子的出射速度分布可以采用麦克斯韦分布模型,而出射角度分布可近似采用(0,δmax]均匀分布模型进行处理,采用数值计算的方法可得到高、低能态氢原子的横向偏移r的分布模型.
3)在距泡口中心处一个很小的范围rc内,低能态原子分布概率为0,而高能态原子概率最大,该半径是设计储存泡口的重要参数,即泡口优化半径.
4)聚焦距离l3越小,泡口优化半径rc越小,且优化半径和聚焦距离之间近似呈线性关系.
5)实际设计的聚焦距离越小,越有利于被动型氢原子钟的小型化.但是泡口加工的尺寸精度要求越高,增加了加工难度,所以应综合考虑聚焦距离和泡口直径,以及其对系统弛豫时间的影响,图9中的数量关系为设计提供了依据.
References)
[1]Vanier J,Audoin C.The quantum physics of atomic frequency standards [M]. Bristol, UK: Adam Hilger,1989.
[2]Busca G,Wang Q,Belloni M,et al.Cavity pulling in Galileo passive hydrogen maser[C]//IEEE Proceedings of International Frequency Control Symposium.Florida,USA,2003:86-89.
[3]Droz F,Mosset P,Wang Q,et al.Space passive hydrogen maser—performances and lifetime data[C]//IEEE Proceedings of International Frequency Control Symposium.Besancon,France,2009:393-398.
[4]Goldenberg H M,Kleppner D,Ramsey N F.Atomic hydrogen maser[J].Physical Review Letters,1960,5(8):361-362.
[5]Peters H E.Magnetic state selection in atomic frequency and time standards[C]//Proceedings of the 13th Annual Precise and the Time Interval Applications and Planning Meeting.Washington,DC,USA,1981:645-661.
[6]张为群,代克,张燕军.氢脉泽中四极磁态选择器的设计及其应用[J].量子电子学报,2008,25(1):38-42.Zhang Weiqun,Dai Ke,Zhang Yanjun.Design of 4-pole magnetic selector in hydrogen atom [J].Chinese Journal of Quantum Electronics,2008,25(1):38-42.(in Chinese)
[7]Mattison E M,Vessot R F C,Shen W.Single-state selection system for hydrogen masers[C]//Proceedings of the 40th Annual Frequency Control Symposium.Maryland,USA,1986:422-427.
[8]崔宏宾.原子物理学[M].合肥:中国科学技术大学出版社,2009.
[9]朱宏伟,陈江,张涤新,等.磁选态单束铯束管铯原子速率分布的模拟计算[J].宇航计测技术,2010,30(3):26-28.Zhu Hongwei,Chen Jiang,Zhang Dixin,et al.Simulative calculation about velocity distribution of cesium atom in magnetic state selecting cesium single beam tube[J].Journal of Astronautic Metrology and Measurement,2010,30(3):26-28.(in Chinese)
[10]Wang Q,Mosset P,Droz F.Verification and optimization of the physics parameters of the onboard Galileo passive hydrogen maser[C]//Proceedings of the IEEE 38th Annual Precise Time and Time Interval(PTTI)Meeting.Reston,USA,2006:81-94.

