基于RBF神经网络的快速伺服刀架迟滞特性建模

王晓慧 丁智 刘宝权 王军生 张岩

(1鞍钢股份技术中心，鞍山 114009)(2鞍钢集团自动化公司，鞍山 114009)

在追求产品小型化、集成化的今天，出现了以光学为理论基础，以微机械加工为手段制作的微光机电一体化系统，并被广泛应用于信息处理、空间技术、光纤通讯等诸多领域［1］.而具有微结构表面的光学元件由于其光学特性、摩擦性、耐磨损性等特定性能，已经成为微光机电产品的关键零部件［2-3］.由于传统机床很难满足微结构表面车削加工过程中对系统高频响、高分辨率、高次轨迹联动功能的要求，近年来，利用快速伺服刀架(FTS)作为精密微位移加工模块来车削加工微结构表面的方法已经成为微结构表面切削加工的一种主流技术［4-6］.压电陶瓷由于具有分辨率高、响应快、刚度大等优点，成为常用的FTS驱动元件，但是压电陶瓷本身所固有的迟滞、蠕变等非线性特点不但会降低FTS系统的控制精度，而且可能造成系统失稳［7］.为了减小迟滞非线性的影响，提高 FTS的跟踪控制精度，必须对其进行合理建模，从而设计相应的控制策略.近年来，针对精密制造系统中迟滞非线性系统的建模日益成为各国学者关注的焦点.文献［8］在经典Preisach模型的基础上建立了广义Preisach模型，大幅度提高了压电陶瓷的跟踪精度.文献［9-10］将神经网络引入到迟滞非线性的建模中，通过引入Preisach型迟滞算子的概念，利用神经网络来离散化Preisach模型，简化模型的辨识过程.但是由于Preisach模型属于静态模型，即迟滞输出仅仅受到输入极值的影响，而与输入信号的变化频率无关，即速率无关(rate-independent)，很难精确地对快速伺服刀架(FTS)的动态迟滞特性进行建模.因此，针对FTS的动态迟滞特性，本文建立了FTS迟滞系统的RBF神经网络模型.由于理论上神经网络不能辨识压电陶瓷驱动器的迟滞特性这类多值映射的非线性现象［11］，因此本文采用拓展输入空间的方法通过引入指数型迟滞算子，将迟滞算子的输出与FTS系统的输入一起作为RBF神经网络的输入向量，实现FTS迟滞系统由多值映射到单值映射的转换，进而利用神经网络对其进行建模.

1 快速伺服刀架动态迟滞特性

快速伺服刀架作为微结构表面车削加工的关键部件，其具体结构如图1所示.系统选用德国PI公司的P-841.20型压电陶瓷作为FTS的驱动元件，其最大伸长量为30 μm，分辨率可达0.3 nm，空载频响为14 kHz，采用德国PI公司的D-050型电容测微仪作为其实时位移检测装置，其量程为50.8 μm，测量分辨率为0.1 nm.

图1 快速伺服刀架结构示意图

快速伺服刀架的迟滞特性主要体现在其电压位移曲线.由图2可见，FTS在开环状态下其升压位移曲线与降压位移曲线并不一致，同样的输入电压因为加压历史的不同对应不同的输出位移，同样的输出位移对应不同的输入输出曲线，而且其迟滞曲线宽度随着输入电压幅值的增加而增大.

FTS的动态迟滞非线性特点体现在其驱动电压频率依赖性上，即速率相关(rate-dependent)性.改变输入信号频率，幅值60 V，输入频率分别为0.1，1.0，2.5，5 Hz，测试其输入输出特性，如图3所示，随着输入电压频率的改变，FTS迟滞曲线的形状和宽度也随之改变.随着输入电压信号频率的增加，其最大输出位移值也随之变小，频率为0.1 Hz输入信号的最大输出位移值比频率为5 Hz输入信号的最大输出位移值大0.2 μm左右；同时，随着输入信号频率的增加，其迟滞曲线的宽度也略有增加.

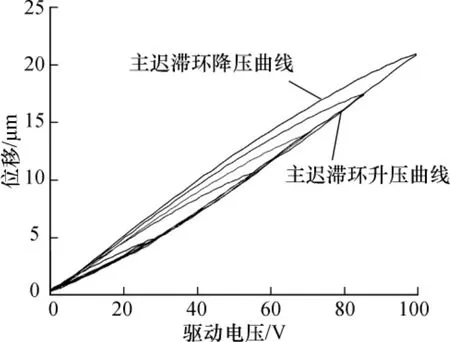
图2 FTS迟滞位移曲线

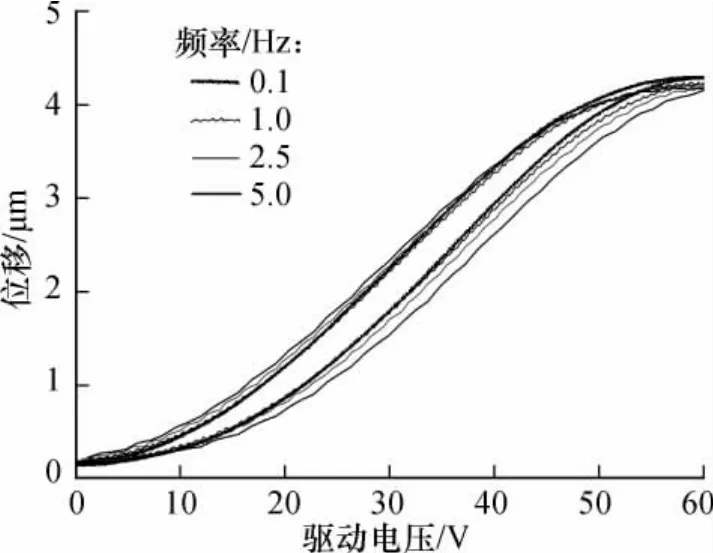
图3 FTS输出频率特性

由此可见，FTS的输出位移不仅与当前输入电压和历史输入电压有关，还与输入电压信号的频率有关，其动态迟滞特性是具有速率相关性的典型多对多非线性映射问题.因此，建立能够描述其动态迟滞特性，并具有常规逼近技术优点的迟滞模型是本文所做的研究工作.

2 基于RBF神经网络的FTS迟滞模型

2.1 拓展输入空间

FTS的迟滞特性是一个多值映射问题，假设输入输出信号分别满足u≤C1，y≤C2其中C1，C2为常数，多值迟滞映射定义如下:

定义1 y=f(u(t))为多值映射迟滞函数，如果满足以下条件:

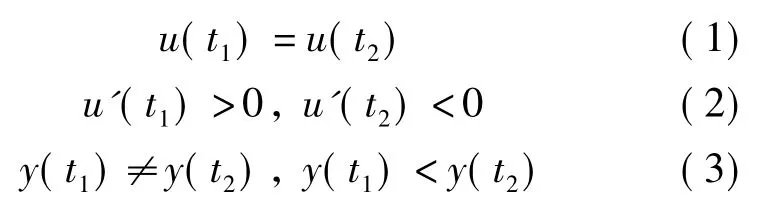
式中，t1，t2表示在输入值u大小相同时，正、逆程对应的时间；y(t1)表示输入为u(t1)时的y值.对于极值时对应的特殊点(见图4)满足:

t1=t2，u(t1)=u(t2)，y(t1)=y(t2)=y(t*)

图4 多值映射迟滞特性

通过分析FTS系统的迟滞位移曲线发现，虽然迟滞曲线的形状受到输入信号幅值及频率的影响，但是曲线上动点的运动规律却是非常的接近，在输入到达某一极值点的前后分别沿着类似的两条曲线运动.根据迟滞曲线的这一特点，可以用形状相似的数学曲线，即构造迟滞算子f(x)来描述系统的迟滞动态特性.这里利用指数函数来构造迟滞算子，其数学表达式为

式中，x为系统输入；f(x)为迟滞算子输出；x0为距离x最近的前一个输入极值；f(x0)为输入为x0时迟滞算子的输出.

为了更好地跟踪不同形状迟滞曲线的变化趋势，对迟滞算子进行了如下改进:

在式(4)中，由于σ的值恒为1，很难对不同形状的迟滞曲线都进行高精度的辨识，因此增加一个调整迟滞算子曲线形状的系数σ，以便于能够更精确的跟踪迟滞曲线的变化趋势.由式(5)可知

将FTS系统的输入x(t)与迟滞算子的输出f［x(t)］共同作为神经网络的输入向量，神经网络的输入空间就由原来的一维增加到了两维，称之为输入空间的拓展.这样，就可以在多维空间中唯一地确定迟滞特性的每一个状态，建立FTS的迟滞特性模型.

2.2 基于RBF神经网络的迟滞模型

由于径向基函数(RBF)神经网络具有计算量小、收敛速度快、无局部极小等优点，因此本文利用RBF神经网络作为迟滞非线性系统的建模工具.利用拓展输入空间法建立的FTS迟滞模型基本结构如图5所示，将FTS系统输入x(t)与迟滞算子输出f［x(t)］一同作为RBF神经网络的输入向量.

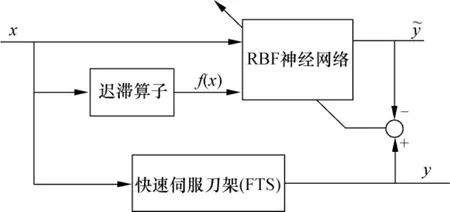
图5 拓展输入空间法建立FTS系统迟滞模型

3 模型的仿真研究

为了验证模型的有效性，对FTS系统施以频率为1 Hz，幅值为0～60 V的正弦周期激励，采样频率为1 kHz，采集2000个实测数据对，随机挑选其中的1500个数据对用来训练神经网络，其余500个数据对用来检验模型效果.由于采集的数据单位不一致且均为正值，因而在训练之前必须对数据进行归一化处理，归一化后的数据将分布在［0，1］区间内.利用拓展输入空间法进行系统辨识的结果如图6(a)所示.图6(b)为实测数据的辨识误差，模型的验证均方差MSE=5.1633×10－6.

图6 RBF神经网络模型的辨识结果及误差

4 结语

本文针对快速伺服刀架(FTS)的动态迟滞特性，通过引入指数型迟滞算子，采用拓展神经网络输入空间的方法成功实现了FTS迟滞系统由多值映射到单值映射的转换，并利用RBF神经网络对其进行建模.实验结果表明，该迟滞模型可以很好地预测快速伺服刀架的迟滞特性，模型的验证均方差MSE为5.1633×10－6.

References)

［1］王仕璠，朱自强.现代光学原理［M］.成都:电子科技大学出版社，1998:2-12.

［2］Asoh H，Oide A，Ono S.Formation of microstructured silicon surfaces by electrochemical etching using colloidal crystal as mask［J］.Electrochemistry Communications，2006，8(12):1817-1820.

［3］Huang Ying，Liu Ran，Lai Jianjun，et al.Design and fabrication of negative microlens array［J］.Optics＆Laser Technology，2008，40(8):1047-1050.

［4］Sze-Weia Gan，Han-Seok Lim，Rahman M，et al.A fine tool servo system for global position error compensation for a miniature ultra-precision lathe［J］.Machine Tools and Manufacture，2007，47(7/8):1302-1310.

［5］Gao W，Tano M，Takeshi A，et al.Measurement and compensation of error motions of a diamond turning machine［J］.Precision Engineering，2007，31(3):310-316.

［6］杨元华.基于FTS的微结构功能表面超精密切削加工关键技术［D］.哈尔滨:哈尔滨工业大学，2007.

［7］Li Chuntao，Tan Yonghong.A neural networks model for hysteresis nonlinearity［J］.Sensors and Actuators，2004，7112(3):49-54.

［8］Ge P，Jouaneh Musa.Generalized preisach model for hysteresis nonlinearity of piezoceramic actuators［J］.Precision Engineering，1997，20(2):99-111.

［9］Adly A A，Abd-El-Hafiz S K.Using neural networks in the identification of preisach-type hysteresis models［J］.IEEE Trans Magnetics，1998，34(3):629-635.

［10］Claudio S，Ciro V.Magnetic hysteresis modeling via feed-forward neural networks［J］.IEEE Trans Magnetics，1998，34(3):623-628.

［11］Wei J D，Sun C T.Constructing hysteretic memory in neural networks［J］.IEEE Trans Systems，Man and Cybernetics Part B:Cybernetics，2000，30(4):601-609.