基于对称扩展DFT变换的OFDM系统信道估计方法

巴特尔 江 彬 范晓俊 刘远龙 仲 文 高西奇

(东南大学移动通信国家重点实验室，南京 210096)

随着LTE协议标准的形成，LTE系统已经逐渐逼近商用，LTE下行链路采用正交频分复用(orthogonal frequency division multiplexing，OFDM)传输方案.OFDM技术具有高传输带宽、高传输效率以及能有效对抗多径衰落的特点［1］，已被多种无线传输标准采纳为关键链路技术.

OFDM系统的相干接收需要精准的信道信息.通过在OFDM符号的固定子载波上插入已知导频获得导频子载波上的信道响应，并通过后续插值获得非导频子载波上的信道响应，这种方法被称作导频辅助的信道估计方法［2-3］.在众多估计方法中，线性最小均方误差(linear minimum mean square error，LMMSE)信道估计方法由于其具有最优的MSE性能而受到广泛的关注.LMMSE估计使用了导频子载波上信道的自相关信息，在计算中涉及复杂的矩阵求逆和相乘，因此具有较高的实现复杂度.文献［4-5］提出在 DFT(discrete Fourier transformation)变换信道估计方法，利用信道时延扩展小于导频子载波数的特性，可以有效地降低实现复杂度.在实际传输系统中常为了避免在接收端的频谱混叠而引入虚载波，虚载波的存在使得DFT变换后的信道参数出现了“频谱泄漏”，严重恶化了边缘子载波的估计性能.使用DCT(discrete cosine transformation)变换信道估计方法［6-7］可以有效地缓解这一问题，但DCT变换本身也具有较高的计算复杂度.为此，本文对DFT变换信道估计方法进行改进，提出了一种基于对称扩展DFT变换的信道估计方法，可以用接近DFT变换信道估计方法的实现复杂度，逼近DCT变换信道估计方法的性能.

1 系统模型及DFT信道估计方法

1.1 OFDM系统模型

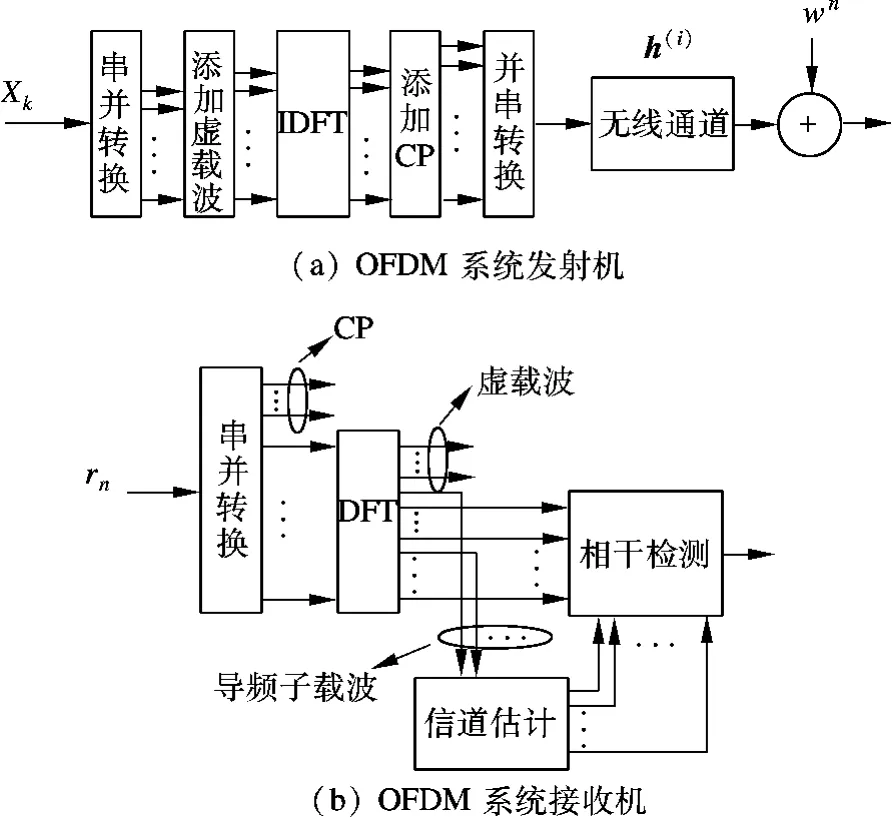
图1 OFDM系统原理框图

假设一包含N个子载波的OFDM传输系统，其发送端原理框图如图1(a)所示［3］，发送端有M(M≤N)个发送数据符号，经过串并转换和载波映射，形成长度为N的发送频域数据.为避免在接收端引起频谱混叠，频带边缘的N－M个子载波保留不用，这些不传输数据的子载波被称作虚载波(virtual subcarriers);频域发送数据再经过N点IDFT变换，添加循环保护前缀(cyclic prefix，CP)并作并串转换之后，被发送到无线信道中.CP的作用是消除由多径信道带来的符号间干扰(inter symbol interference，ISI)，因此 CP的长度应满足LCP＞LCH，即 CP的长度大于信道的时延扩展.OFDM系统接收机如图1(b)所示，假设接收端已获得准确的定时信息，接收数据在去除CP后被送至DFT模块进行OFDM解调.假设时域信道参数h(i)在一个OFDM符号间隔内保持不变，记为

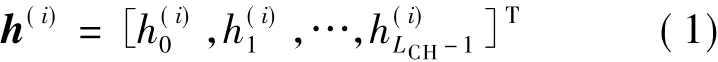
在OFDM解调之后第i个OFDM符号第k个子载波上的输出Y(i)k可以记为

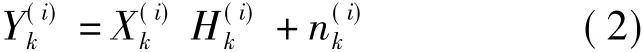
为简便起见，后文中忽略OFDM符号标识i.

相干接收需要精准的信道信息，假设在发送端已知导频符号被插入在数据符号中一起发送，导频数量为NP，并被等间隔地插入在固定载波{kn;0≤n≤NP－1}上，如图 2 所示.令 XP=［Xk0，Xk1，…，XkNP－1］T为发送导频符号组成的向量，YP=［Yk0，Yk1，…，YkNP－1］T为接收端 OFDM 解调之后导频子载波上输出频域信号所组成的向量，nP=［nk0，nk1，…，nkNP－1］T为导频子载波上频域噪声组成的向量，由式(2)和(3)可得

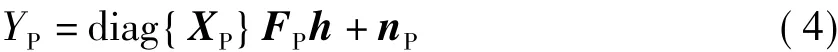
式中，FP是一个NP×LCH维矩阵，其元素可以表示为［3］

向量nP为零均值高斯分布，其自相关阵为

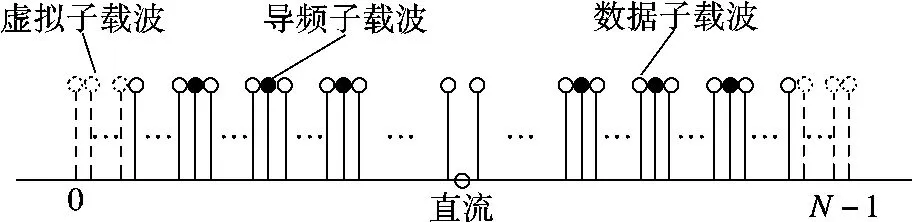
图2 OFDM系统载波映射

式中，INP表示NP维单位阵;diag{a}表示以向量a为对角元素的对角阵.令 HP=［Hk0，Hk1，…，HkNP－1］T为由导频子载波上的频域信道响应组成的向量，由式(3)可知

式中，Copt为一个NP×NP维滤波矩阵，其表达式为

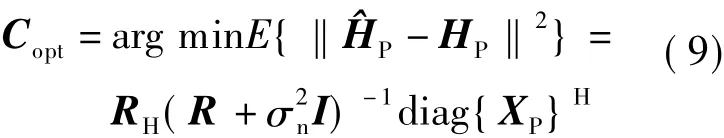
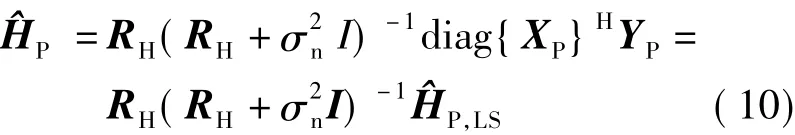
即式(10)为关于导频子载波的LMMSE信道估计的表达式.式中，为导频子载波上的最小二乘(LS)信道估计，记为

LMMSE估计的求解过程涉及一个Np×Np维矩阵的求逆，计算复杂度较高，因此有必要寻求简化方法以降低其计算复杂度.

1.2 传统DFT信道估计

通常情况下，信道时延扩展的长度小于导频子载波的个数，即LCH＜NP，因此如果将式(10)转换至时域进行，利用时域的能量集中特性以及FFT的高效实现，可以在保证估计性能的同时，有效地降低实现复杂度［4］.将导频子载波上的LS估计变换至时域，表示为

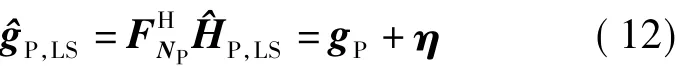
式中，FNP为Np×Np维的归一化DFT变换矩阵，H为其反变换;为导频子载波所对应的时域部分信道响应，为了与整个频带上的宽带时域信道h做区分，用g来表示;η=为变换后的噪声，正交变换不改变其统计特性.在时域对进行LMMSE滤波后再变换回频域，得到最终的估计结果，上述过程可以记为

式中，Γtd为时域滤波矩阵，结合式(10)和(11)，可以表示为

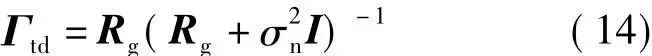
DFT变换信道估计的几种简化形式和性能见文献［4］.

观察gP中的元素，将其表示为

式中，α=M/N，表示有用子载波占总子载波数的比例;k0表示第1个导频子载波的序号.从式(16)可以看出，当虚载波不存在，即α=1时，时域部分信道响应 gP，n将仅在 n∈［0，L －1］区间内有值;当虚载波存在，即α≠1时，原本集中在L个抽头上的能量会“扩散”到gP，n所有的抽头上去，如图3所示，此时，噪声和扩散的能量将会混叠在一起变得不可分辨.因此，虚载波的存在导致频谱扩散问题，严重影响了DFT变换信道估计的性能.

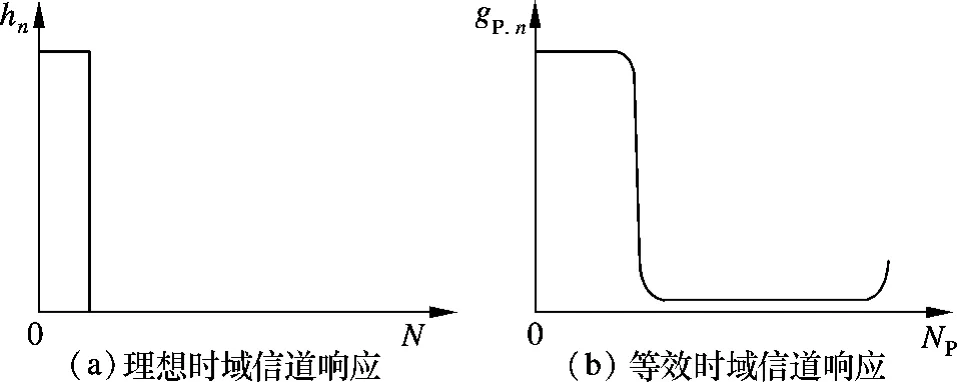
图3 虚载波的影响

文献［6-7］提出了基于DCT变换的信道估计方法，与DFT变换相比，DCT变换通过镜面扩展消除了边界上的不连续性，具有更好的能量集中特性和更低的频谱能量泄漏，此外DCT变换还有更好的解相关性能.因此，在有虚载波的OFDM系统中，DCT变换信道估计可获得更好的估计性能，但其实现复杂度要高于DFT信道估计方法.

2 基于对称扩展DFT变换的信道估计

2.1 SE-DFT信道估计

针对虚载波引起的频谱泄漏问题，本文提出一种基于对称扩展(symmetric extension，SE)DFT变换的信道估计方法，相比于传统DFT变换信道估计方法，本文方法可以在几乎不增加系统实现代价的同时，逼近DCT变换信道估计方法的性能.

对称扩展DFT变换信道估计的系统结构如图所示，在获得导频子载波上的LS信道估计之后，将LS估计值做对称扩展，表示为

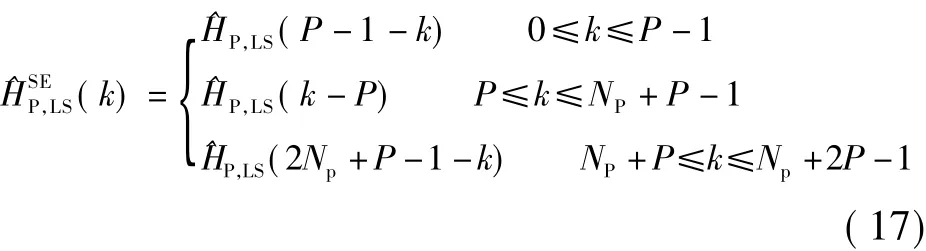
式中，P为单边扩展点数，式(17)也写为向量形式

式中，Θse=ΘPΘme，其中 Θme的具体形式为

式中，JNp表示反对角线上元素均为1、其余元素均为0的Np×Np维矩阵;ΘP的具体形式为

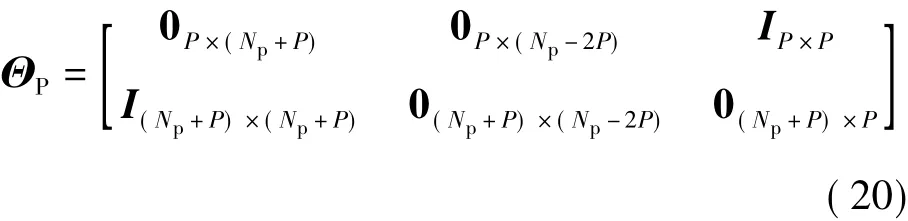
图4 对称扩展DFT变换信道估计原理框图

从式(20)可以看出，对称扩展过程可以分解为先将序列做镜面扩展(mirror extension，ME)，然后循环位移P点，最后加窗截短为NP+2P点.因此，对称扩展序列可以看作是镜面扩展序列［5］经过一个滤波器滤波之后的结果.通过文献［9］可知镜面扩展序列的DFT变换与原序列DCT变换之间存在等价关系，因此SE-DFT序列也可以看作为原序列的DCT变换滤波之后的结果.实际上，通过后续的仿真结果可以发现，当扩展点数P=Np/2时，SE-DFT信道估计与DCT信道估计具有相同的性能.

类似地，对扩展后的序列在SE-DFT变换后进行LMMSE滤波，以获得更为精准的估计结果，最后对滤波结果做反变换即可得到对称扩展的信道估计，该过程可以记为

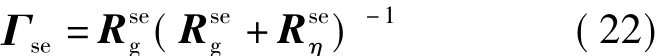
由于对称扩展的关系，在原来相互无关的序列上引入了相关性，不再是一个对角阵.

如前所述，为进一步降低计算复杂度，将Γse简化为一个对角阵，即

最后，在获得了关于导频子载波对称扩展DFT变换信道估计之后，可以简单地将扩展出来的点去除，随后通过插值即可获得其他数据子载波上的信道响应.插值也可以通过对称扩展IDFT来进行，然后将扩展出来的点去除.

2.2 复杂度分析

在式(21)所描述的SE-DFT信道估计方法中，如果采用式(24)所定义的变换滤波矩阵，其实现复杂度主要取决于DFT变换.快速傅里叶变换(FFT)使得 DFT变换广泛应用，Cooley等早在1964年提出应用于变换长度为2n情况下的基－2算法［10］，其后在此基础之上又发展出了混合基(mix-radix)算法和分裂基(split-radix)算法［11］，使得FFT算法可以应用在更一般的情况下.使用不同的实现算法，其计算复杂度也会有所不同，此外不同基的实现效率也有所不同.为便于比较，可以近似地将DFT算法的计算复杂度计为Nlog2N次复数乘法.对于SE-DFT而言，其计算复杂度为(N+2P)log2(N+2P)，当扩展的点数P较小时，由于扩展而带来的复杂度的增加是可以忽略不计的.实际上，由于不同基的实现效率并不相同，因此在某些特殊情况下，对称扩展反而可以提高实现效率.在实际应用中根据导频序列的长度灵活选择扩展点数，可以在提高性能的同时，保证较高的实现效率.

3 仿真结果

仿真基于LTE下行链路系统模型，系统参数如表1所示.信道模型采用抽头延时线模型，延时功率谱采用LTE协议中定义的EPA(extendedpedestrian A)信道模型.EPA信道模型是一个7径信道，每径所对应的时延和该径上的相对功率如表2所示.在本文中，只考虑导频子载波上的MSE性能，并使用归一化的MSE(NMSE)作为评价标准，NMSE的定义为

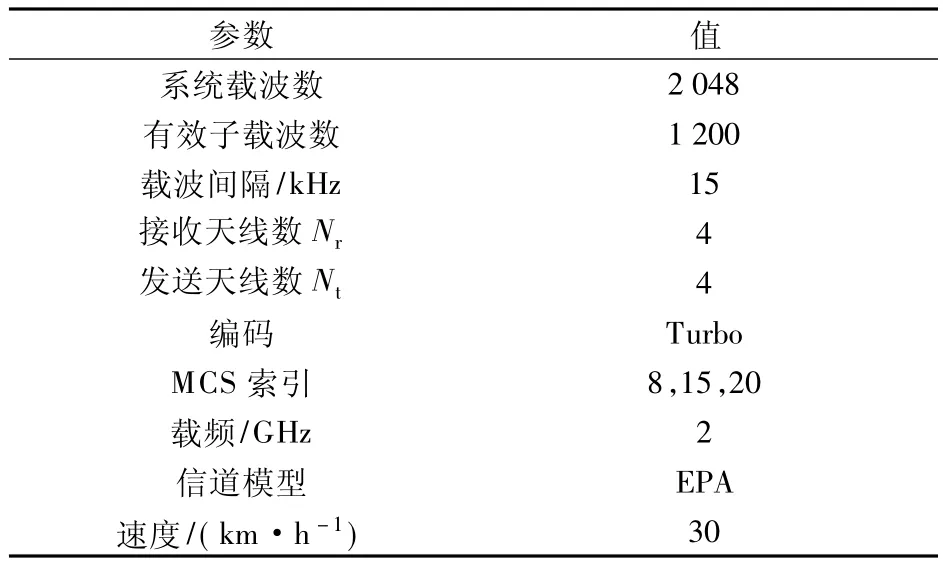
表 系统仿真参数

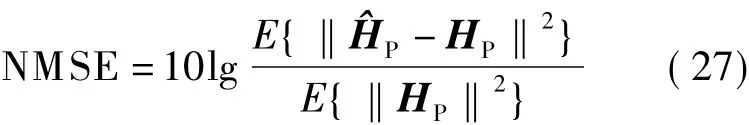
表2 EPA信道模型

3.1 不同子载波上的MSE性能

对于导频在频域等间隔分布的OFDM系统而言，虚载波的存在会使传统DFT变换信道估计方法的MSE性能在频带的边缘显著恶化，严重降低边缘子载波上传输的可靠性.通过对称扩展，可以有效地改善这一问题.图5给出了扩展点数为1，Np/4及Np/2三种情况下不同导频子载波上的MSE性能.图6给出了不同扩展点数与所有导频子载波上平均NMSE性能之间的关系.从图5中可以看到，即使扩展点数为1也可以显著地提高边缘子载波的MSE性能.从图6可以看到:① 不扩展时，其性能与 DFT变换信道估计方法相同;②只要扩展较少的点数，即可获得明显的性能增益;③随扩展点数的增加，其MSE性能逐渐提高，当P=Np/2时，其性能与DCT变换信道估计方法相同.

图5 不同子载波上的MSE性能(SNR=15 dB)

图6 不同扩展点数下的MSE性能(SNR=15 dB)

3.2 信道估计整体性能

图7比较了导频点上的LS、DFT变换、DCT变换以及SE-DFT变换等几种不同信道估计方法的性能，其中，LS信道估计采用式(11)进行计算，DFT变换信道估计采用式(13)，并将Γtd简化为对角阵，如式(15)所示.DCT变换信道估计的公式与式(13)类似，但其正交变换为DCT变换，可以表示为

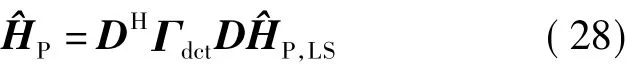
式中，D为归一化DCT-Ⅱ变换矩阵，DH为其反变换;Γdct为DCT滤波矩阵，也将其简化为对角阵的形式，即定义为

图7 不同信道估计方法的NMSE性能比较

通过图7可以看出，即使在扩展点数为1的情况下，所提SE-DFT信道估计方法也能获得2 dB左右的性能增益，此时的性能增益主要来自于对边缘子载波性能的改善.当扩展点数为Np/2时，其性能与DCT变换信道估计完全相同，这也与图5和图6中的仿真结果一致.

图8在LTE下行链路中评估了不同方法对接收机性能的影响，LTE下行链路的参数如表1所示，其导频数为200，假设扩展点数P=28，这样在经过SE扩展之后的序列长度为256，可以使用高效率的基4-FFT算法来实现;接收机使用LMMSE并行迭代软干扰抵消算法，迭代次数为4;为提高接收机性能，采用频域跳频以获得频率分集增益;分别仿真了MCS(modulation and coding scheme)=8，15和20三种情况，与之对应的调制方式分别为QPSK，16QAM 和64QAM，码率分别为0.58，0.60和0.55;发送层数为4，采用LTE协议中定义的开环方式进行传输;在获得了导频点上的信道估计之后，时间域采用线性插值，频率域采用样条插值来获得数据子载波上的信道响应.从仿真结果中可以看出，使用SE-DFT变换信道估计的接收机，在64QAM调制下其性能与使用DCT变换信道估计的接收机相差在0.3 dB以内;在 QPSK和16QAM调制方式下，其性能与使用DCT变换信道估计的接收机性能一致.

图8 使用对称扩展DFT变换信道估计器的接收机性能

4 结语

针对有虚载波的OFDM传输系统，提出了一种基于对称扩展DFT变换的信道估计方法.相对于传统的DFT变换信道估计方法，该方法可以在几乎不增加复杂度的情况下，有效解决由虚载波带来的边缘子载波性能恶化问题，提高信道估计的性能，只需扩展较少的点数，即可逼近DCT信道估计的性能.

References)

［1］ Bingham J A C.Multicarrier modulation for data transmission:an idea whose time has come［J］.IEEE Communications Magazine，1990，28(5):5-14.

［2］ Li Ye.Pilot-symbol-aided channel estimation for OFDM in wireless systems［J］.IEEE Trans on Veh Technol，2000，49(4):1207-1215.

［3］ Morelli M，Mengali U.A comparison of pilot-aided channel estimation methods for OFDM systems［J］.IEEE Trans on Signal Processing，2002，49(12):3065-3073.

［4］ Edfors O，Sandell M，van de Beek J J，et al.Analysis of DFT-based channel estimators for OFDM ［J］.Wireless Personal Communications，2000，12(1):55-70.

［5］ Wang Yi，Li Lihua，Zhang Ping，et al.DFT-based channel estimation with symmetric extension for OFDMA systems［J］.EURASIP Journal on Wireless Communications and Networking，2009，2009(1):647130.

［6］Yeh Y H，Chen S G.DCT-based channel estimation for OFDM systems［C］//IEEE International Conference on Communications.Paris，France，2004:2442-2446.

［7］Jiang B，Wang W，Wang H M，et al.Two dimensional DCT-based channel estimation for OFDM systems with virtual subcarriers in mobile wireless channels［C］//IEEE International ConferenceonCommunications.Beijing，China，2008:3801-3806.

［8］Kay S M.Fundamentals of statistical signal processing:estimation theory［M］.New Jersey，USA:Prentice Hall Press，1987.

［9］ Oppenheim A V，Schafer R W.Discrete-time signal processing［M］.3rd ed.New Jersey，USA:Prentice Hall Press，2009.

［10］Cooley J W，Tukey J W.An algorithm for the machine calculation of complex fourier series［J］.Math Comput，1964，19(90):297-301.

［11］ Singleton R.An algorithm for computing the mixed radix fast fourier transform ［J］.IEEE Trans on Audio and Electro Acoustics，1969，17(2):93-103.