酿酒葡萄与葡萄酒理化指标的联系分析

薛凌云 刘洋洋

（河南师范大学计算机与信息工程学院 河南 新乡 453007）

1 模型准备

1.1 主成分分析算法

主成分分析是一种通过降维技术把多个变量化为少数几个主成分（即综合变量）的多元统计方法，这些主成分能够反映原始变量的大部分信息，通常表示为原始变量的线性组合[1]主成分分析的基本原理为：

假定有样本，每个样本共有p个特征，构成一个n×p阶的数据矩阵：

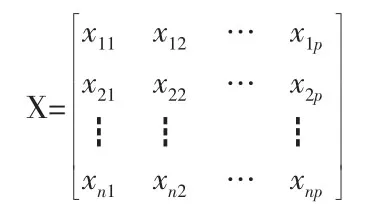
当p较大时，在p维空间中考察问题比较麻烦。为了克服这一困难，就需要进行降维处理，即用较少的几个综合指标代替原来较多的变量指标，而且使这些较少的综合指标既能尽量多地反映原来较多变量指标所反映的信息，同时它们之间又是彼此独立的。

记 x1，x2，…，xp为原变量指标，z1，z2，…，zm（m≤p）为新变量指标：

从以上的分析可以看出，主成分分析的实质就是确定原来变量xj（j=1，2，…，p）在诸主成分 zi（i=1，2，…，m）上的荷载 lij（i=1，2，…，m；j=1，2，…，p）。从数学上可以证明，它们分别是相关矩阵m个较大的特征值所对应的特征向量。主成分分析的步骤为：

步骤一：计算相关系数矩阵：

rij（i，j=1，2，…，p）为原变量 xi与 xj的相关系数，rij=rji，其计算公式为：

步骤二：计算特征值与特征向量：

分别求出对应于特征值 λi的特征向量 ei（i=1，2，…，p）i，要求‖ei‖=1，即，其中eij表示向量ei的第j个分量。

计算主成分贡献率及累计贡献率：

贡献率：

累计贡献率：

一般取累计贡献率达85%～95%的特征值 λ1，λ2，…，λm所对应的第 1、第 2、…、第 m（m≤p）个主成分。

计算主成分载荷：

各主成分的得分：

1.2 典型相关分析算法

典型相关分析就是利用综合变量对之间的相关关系来反映两组指标之间的整体相关性的多元统计分析方法。它能够揭示出两组变量之间的内在联系。

典型相关分析的基本思想和主成分分析非常相似。其目的是识别并量化两组变量之间的联系，将两组变量相关关系的分析化为一组变量的线性组合与另一组变量线性组合之间的相关关系分析。它的基本原理是：为了从总体上把握两组指标之间的相关关系，分别在两组变量中提取有代表性的两个综合变量，利用这两个综合变量之间的相关关系来反映两组指标之间的整体相关性。

首先在每组变量中找出变量的一个线性组合，使得两组的线性组合之间具有最大的相关系数。然后选取相关系数仅次于第一对线性组合并且与第一对线性组合不相关的第二对线性组合，依次类推下去，直到两组变量之间的相关性被提取完毕为止。被选出的线性组合配对称为典型变量，它们的相关系数称为典型相关系数。典型相关系数反映了这两组变量之间联系的强度。

设 X=[x，x，…，x]，Y＝[y，y，…，y]是两个相互关联的随机向量，分别在两组变量中选取若干有代表性的综合变量Mi，Ni使得每一个综合变量是原变量的线性组合。

在确保典型变量保持唯一性时，取方差为1的X、Y的线性函数a1X与b1Y，求使得它们相关系数达到最大的这一组。若存在常向量a1、b1，在a1X与b1Y的方差相等且为1情况下，使得相关系数ρ（a1X，b1Y）达到最大，则称a1X与b1Y是X与Y的第一对典型相关变量。求出第一对典型相关变量之后，可以类似的求出各对之间互不相关的第二对典型相关变量、第三对典型相关变量……。这些典型相关变量就反映了X、Y之间的线性相关情况。我们可以通过检验各对典型相关变量相关系数的显著性，来反映每一对综合变量的代表性，如果某一对的相关程度不显著，那么这对变量就不具有代表性，不具有代表性的变量就可以忽略。这样就可以通过对少数典型相关变量的研究，代替原来两组变量之间的相关关系的研究，从而容易找到问题的本质。

对于X（有p个分量）、Y(有q个分量）两组变量，假设p≤q。则

其中 V11＝Cov（X），V12＝V21＝Cov（X，Y），V22＝Cov（Y）即将总的样本协方差分为第一组变量X的协方差阵V11，两组变量之间的协方差阵V12和V21以及第二组变量Y的协方差阵V22。计算p×p阶矩阵和q×q阶矩阵可以证明，矩阵A和B具有相同的非零特征根，且非零特征根的个数r=rank（A）=rank（B）。

根据证明，矩阵A和B的特征值还具有以下的性质：

（1）矩阵A和B有相同的非零特征值，且相等的非零特征值的数目就等于r；

（2）矩阵A和B的特征值非负；

（3）矩阵A和B的全部特征值均在0和1之间。

1.3 模型的建立与求解

数据采用采用2012年全国数学建模竞赛中A题中数据，利用均值法对（附件2-理化指标）做数据处理，然后运用spass对各个样品葡萄作主成份分析。本操作是选择以特征根大于1为标准提取主成份，或按照累积方差的观点，提取大于80%的值。

对红葡萄主成份分析得到解释的总方差和成分矩阵。分析解释的总方差，此处以特征根大于1或按照累积方差大于80%为标准可以提取7个主成份；然后结合成份矩阵具体提取出花色苷、DPPH自由基、总酚、总糖、还原糖、可溶性固形物、干物质含量7个主成份，在建立典型相关分析模型时以这7种成份作为对红葡萄进行分析的依据。同样的方法，对白葡萄主成份分析得到解释的总方差和成分矩阵。提取出蛋白质、总酚、葡萄总黄酮、总糖、还原糖、可溶性固性物、可滴定酸、固酸比、干物质含量9个主成份，在建立典型相关分析模型时以这9种成份作为对白葡萄进行分析的依据。

对于红葡萄酒的主要成分，提取出附件2中的第一指标及附件3中其成分在各个样品总和相对较高者，得到花色苷、单宁、总酚、酒总黄酮、白藜芦醇、DPPH半抑制体积、辛酸乙酯7中主要成分。

同样的方法，对于白葡萄酒主要成分，提取出单宁、总酚、酒总黄酮、白藜芦醇、DPPH半抑制体积、辛酸乙酯、乙醇、己酸乙酯、癸酸乙酯9中主要成分

根据以上建立的模型，运用matlab[2]对酿红酒葡萄与红葡萄酒所处理过的数据进行求解，采用2012年全国数学建模竞赛中A题中数据，得到矩阵A和矩阵B的特征根及特征向量，由于矩阵A和矩阵B具有相等的特征根，因此可对X、Y两组变量进行典型相关分析，由matlab求解得到7对典型相关变量及典型变量系数和典型相关系数。

第一典型变量：

u1=(1.2549 0.1938-0.2710-0.1240-0.2158 0.2880 0.0489)T

v1=(0.9215 0.3301 0.1270 0.5590 0.1631-1.0091-0.0130)T典型相关系数为：0.9426

M1=1.2549x1+0.1938x2-0.2710x3-0.1240x4-0.2158x5+0.2880x6+0.0489x7

Ni=0.9215y1+0.3301y2+0.1270y3+0.5590y4+0.1631y5-1.0091y6-0.0130y7

第二典型变量：

u2=(-0.7322 0.1994 1.3059 0.1943 0.1144-0.1514 0.0455)T

v2=(-1.0678 0.4214 0.2154 0.3990 0.0236 0.4540 0.0756)T

典型相关系数为：0.8045

M2=-0.7322x1+0.1994x2+1.3059x3+0.1943x4+0.1144x5-0.1514x6+0.0455x7

N2=-1.0678y1+0.4214y2+0.2154y3+0.3990y4+0.0236y5+0.4540y6+0.0756y7

第三典型变量：

u3=(1.1224 0.7326-0.7681 0.1793 0.8618 1.3542-1.3394)T

v3=(0.4000 1.6146-3.2073 0.3965 0.3392 0.8332-0.5788)T

典型相关系数为：0.3604

M3=1.1224x1+0.7326x2-0.7681x3+0.1793x4+0.8618x5+1.3542x6-1.3394x7

N3=0.4000y1+1.6146y2-3.2073y3+0.3965y4+0.3392y5+0.8332y6-0.5788y7

第四典型变量：

u4=(-1.2778-0.8623 0.7279-1.8645 0.0907 1.2485 0.6194)T

v4=(-0.0917-0.5126-0.3531-1.4456-1.2907 2.9930 0.5890)T

典型相关系数为：0.2547

M4=-1.2778x1-0.8623x2+0.7279x3-1.8645x4+0.0907x5+1.2485x6+0.6194x8

N4=-0.0917y1-0.5126y2-0.3531y3-1.4456y4-1.2907y5+2.9930y6+0.5890y7

第五典型变量：

u5=(-0.4807 0.0188-0.1859-0.3014-1.5842-0.2575 2.1840)T

v5=(-0.7746 2.3376 1.4723-0.3571-0.0234-2.8456 0.3208)T

典型相关系数为：0.1163

M5=-0.4807x1+0.0188x2-0.1859x3-0.3014x4-1.5842x5-0.2575x6+2.1840x7

N5=-0.7746y1+2.3376y2+1.4723y3-0.3571y4-0.0234y5-2.8456y6+0.3208y7

第六典型变量：

u6=(-0.6032-0.5175 0.2491-0.0990 0.1455-1.2639 1.6532)T

v6(-0.1013-1.2236 1.8503-2.3064-0.2305 1.8953-0.5177)T

典型相关系数为：0.0973

M6=-0.6032x1-0.5175x2+0.2491x3-0.0990x4+0.1455x5-1.2639x6+1.6532x7

N6=-0.1013y1-1.2236y2+1.8503y3-2.3064y4-0.2305y5+1.8953y6+-0.5177y7

第七典型变量：

u7=(0.8068 1.0451-0.2899-1.4571 0.4521 0.4783 0.3645)T

v7=(-0.6729-0.7583 1.7646 0.8997-0.8239-1.0083-0.3921)T

典型相关系数为：0.0185

M7=0.8068x1+1.0451x2-0.2899x3-1.4571x4+0.4521x5+0.4783x6+0.3645x7

N7=-0.6729y1-0.7583y2+1.7646y3+0.8997y4-0.8239y5-1.0083y6-0.3921y7

由典型变量表达式可得原变量上的负载荷矩阵。

表1 综合变量M的福载荷矩阵

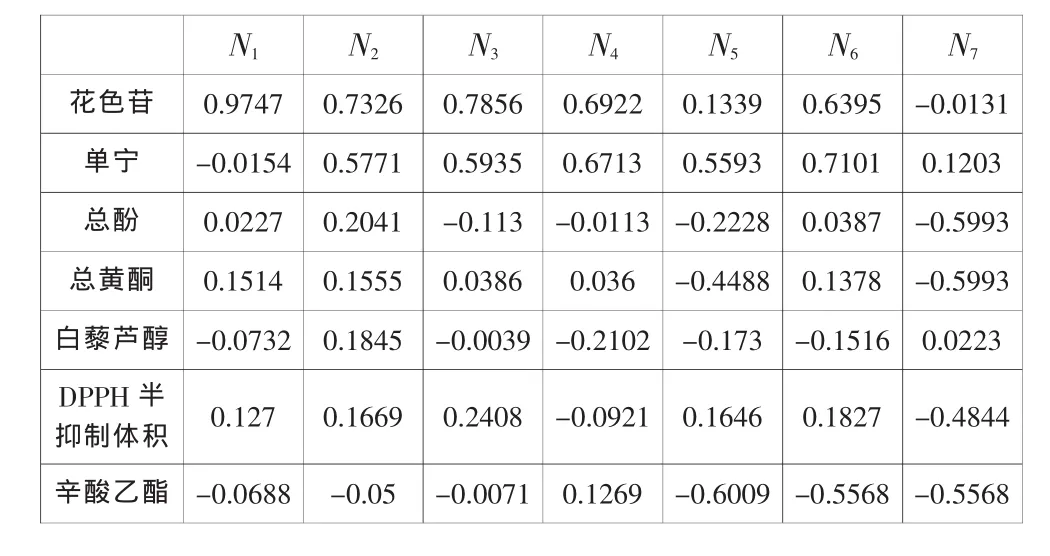
表2 综合变量N的福载荷矩阵

两组变量对的相关性如表3。

表3 红葡萄酒与酿酒葡萄变量对的相关性

由表可知，从第一组典型变量来看，酿酒葡萄理化指标中的花色苷与葡萄酒中花色苷具有极强的相关性；从第二组典型变量来看，酿酒葡萄中DPPH自由基的含量影响到葡萄酒中单宁的含量；第三组典型变量表示的是酿酒葡萄中的总酚与葡萄酒总酚之间的关系，因为相关系数仅为0.3604，相关关系相对较弱；第四组典型变量相关系数为0.2547；第五组典型变量相关系数为0.1163；第六组典型变量相关系数为0.0973，说明可溶性物质和DPPH半抑制体积之间无明显的相关关系；第七组典型变量相关系数为0.0185。典型相关系数逐渐减小，可以忽略后四组典型变量，主要考虑前四组变量中酿酒葡萄与葡萄酒理化指标之间的影响。

用同样的处理过程，对白葡萄酒与酿酒葡萄的理化指标进行典型变量相关分析，得到的结果如表4所示。

表4

从第一组典型相关变量对可看出酿酒葡萄的蛋白质与葡萄酒的单宁含量有很大的相关性；第二组典型相关变量对都为总酚的含量，表明葡萄酒中总酚的含量与所选酿酒葡萄总酚的含量呈比例关系；而后四组变量对典型相关系数均小于0.1，呈现出的相关性不是十分明显，因此可忽略其理化指标之间的影响。

2 结束语

本文将主成分分析与典型相关性分析相结合，将两种模型运用到酿酒葡萄与葡萄酒理化指标的联系分析中去。主成分分析可以将众多的理化指标综合到几个主成分中去，而典型相关性分析则可以分析两个样本的相关性。两种模型有效的结合，对于分析两种样本的联系性有重要的意义。

［1］谢金星，姜启源.数学模型[M].北京：高等教育出版社，2004.

［2］于义良，罗蕴玲，安建业.概率统计与spss应用[M].西安：西安交通大学出版社.