基于抛物线拟合的雷达网时间对准方法研究

李玉琴

（安徽水利水电职业技术学院 安徽 合肥 231603）

0 引言

雷达网中的各部雷达工作时，在时间上通常是不同步的，主要是由以下几个方面的原因造成的：每部雷达的开机时间是不一样的；它们可能有不同的脉冲重复周期和扫描周期，即有不同的采样率；在扫描过程中，来自不同雷达的观测数据通常不是在同一时刻得到的，存在着观测数据的时间差[1]。因此，在融合之前，必须将网内多部雷达的观测数据进行时间对准，即将多部雷达对同一目标不同步的观测数据同步到同一基准时标下。否则，将不同步的观测数据进行融合，融合结果将失去意义。

时间对准的一般做法是：先找出多传感器系统中采样周期最长的一个传感器，然后将该传感器的观测时间序列作为基准时标，将其它传感器的观测数据同步到该基准时标下。目前，时间对准常用的方法有两种：W.D.Blair教授等人提出的最小二乘准则配准法和王宝树教授提出的内插外推法[2]。内插外推法要求目标的运动模型为匀速（CV）模型；最小二乘准则配准法不但要求目标运动模型为匀速模型，而且要求进行对准的两传感器采样周期之比为整数。由此可见，这两种时间对准方法都有其局限性，当目标的运动模型不是匀速模型时，例如对于做机动运动的目标，采用这两种方法的效果往往很差[3]。针对这种情况，本文提出了一种基于抛物线拟合的时间对准方法，在目标做匀加速运动和匀速运动两种情况下，这种方法均可实现观测数据的时间对准，且使得对准后的观测数据更接近真实值。

1 基于抛物线拟合的时间对准方法

1.1 数学模型

给了平面离散点集 Δ={（xi，yi）｜i=0，1，2，…，n}，在某种简易函数类里寻求函数 y＝f（x），使为最小。 这里 y＝f（x）称拟合曲线。当拟合曲线为抛物线时，即 y＝f（x）＝ax2＋bx＋c 时，a，b，c 为下列方程组的解：

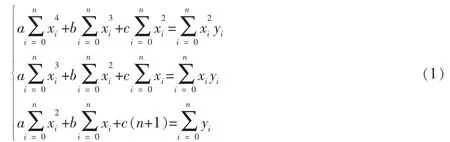
1.2 时间对准方法

为了讨论问题方便，假设雷达网中有A、B两部雷达，雷达A的扫描周期为Ta，雷达B的扫描周期为Tb，且Ta＜Tb，现将雷达A的观测数据对准到雷达B的观测时间序列上来，设雷达A在时刻tai（i＝1，2，…，n）的观测向量为 Zai=[xai，yai，zai]T（i＝1，2，…，n），现在将观测向量 Zai的分量 xai（i＝1，2，…，n）对准到雷达 B 的观测时间序列 tb1，tb2，…，tbn上来，构造拟合抛物线 y＝fx（t）＝axt2＋bxt＋cx，则 ax，bx，cx可由下面的方程组解得：

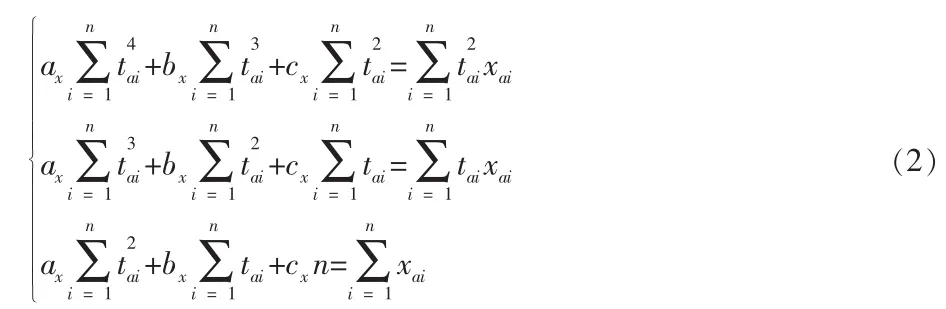
将 t＝tbi（i＝1，2，…，n）代入 y=fx（t）＝axt2＋bxt＋cx中，即可得到雷达 A在时刻tbi的观测向量的x分量的值，此时便完成了两雷达观测向量的x分量的时间对准，同理，可以对雷达A、B观测向量的y、z分量进行时间对准。

2 仿真分析

2.1 目标做匀加速运动的情况

假设雷达网中有A、B两部三坐标雷达，雷达A的采样周期为Ta=3s，距离、方位角和仰角观测误差标准差分别为0.1km、10mrad和10mrad；雷达B的采样周期为Tb=4s，距离、方位角和仰角观测误差标准差与雷达A相同。目标在监视空域内作匀加速直线运动。初始位置为[300km,200km,10km]，速度为[-0.1km/s,-0.1km/s,0km/s]，加速度为[-0.001km/s2,-0.001 km/s2,0 km/s2]。雷达A首次观测到目标的时刻为ta1=0s，雷达B首次观测到目标的时刻tb1=2s，两部雷达的观测结束时刻均为t=330s，故雷达A对目标观测得到111组数据，假设其对应的观测向量为 Za1，Za2，…，Za111，对应的观测时刻为 ta1，ta2，…，ta111；雷达B对目标观测得到83组数据，假设其对应的观测向量为Zb1，Zb2，…，Zb83，对应的观测时刻为tb1，tb2，…，tb83。由于两雷达首次观测到目标的时刻不同，且两雷达采样周期也不同，下面采用抛物线拟合的方法分别将雷达A观测向量序列的x分量序列、y分量序列、z分量序列拟合成一条抛物线，拟合抛物线及目标位置的真实轨迹如图1所示。

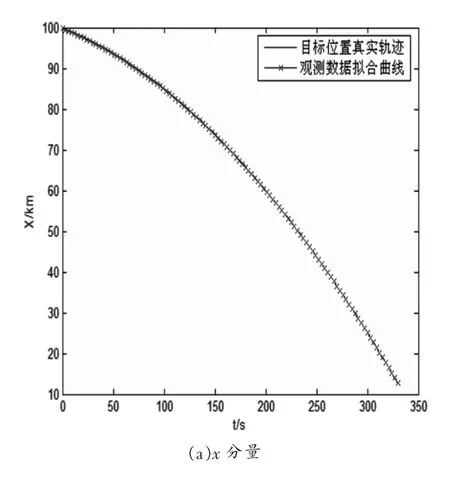
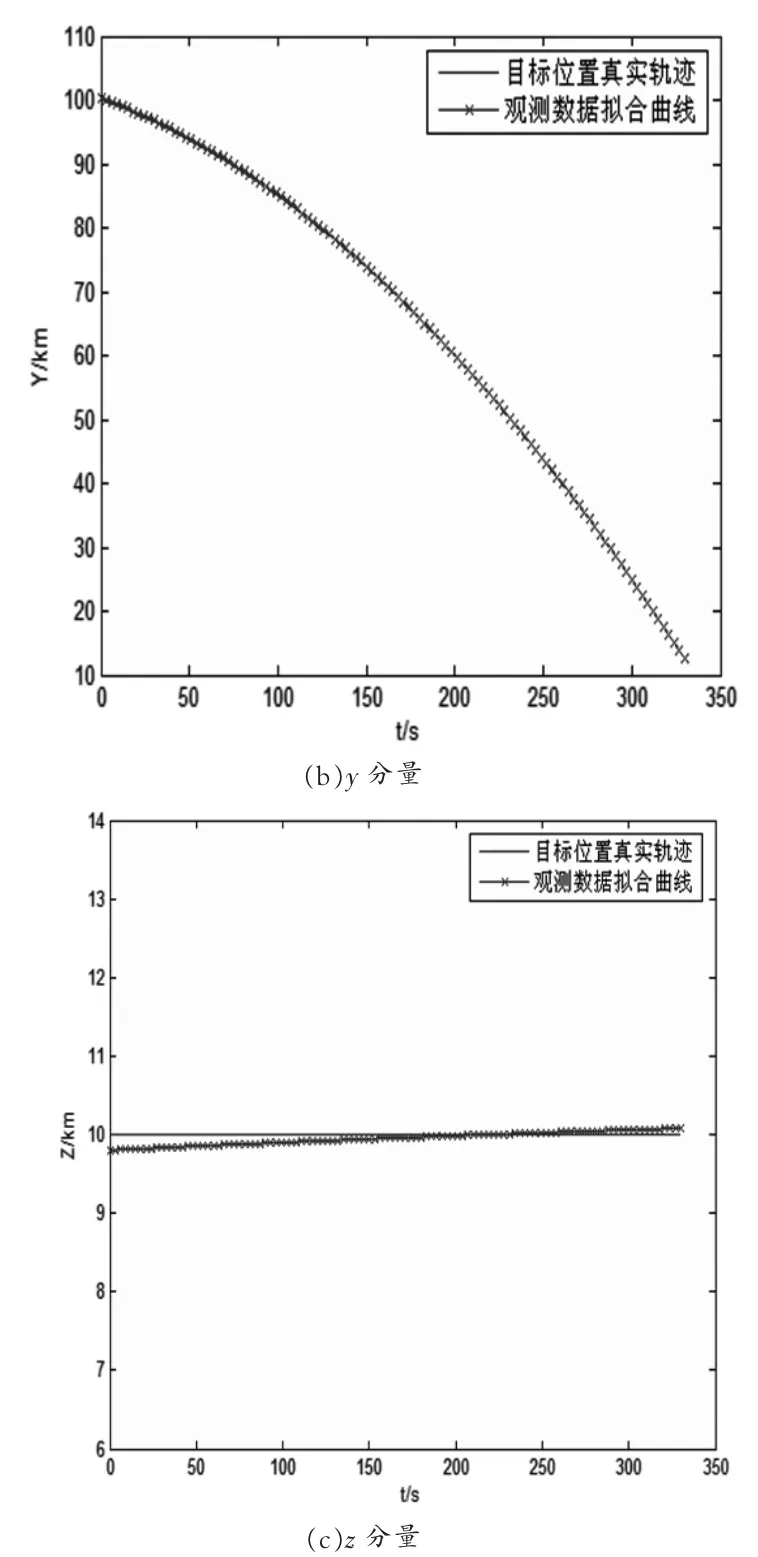
图1 观测数据拟合抛物线

将雷达B对应的观测时刻tb1，tb2，…，tb83代入雷达A观测数据的拟合抛物线所对应的方程中，即可得到与雷达B具有相同采样时刻的数据值，此时偏实现了A、B两雷达观测数据的时间对准。雷达A对雷达B时间对准后的观测数据及雷达B的观测数据如图2所示，可以看出：雷达A时间对准后的观测数据比雷达B的观测数据更接近目标位置的真实轨迹。由于雷达B与雷达A的观测精度相同，故可将雷达B的观测数据看成是雷达A按雷达B的观测时间序列采样得到的数据，所以雷达A时间对准后的观测数据在精度上得到了提高。

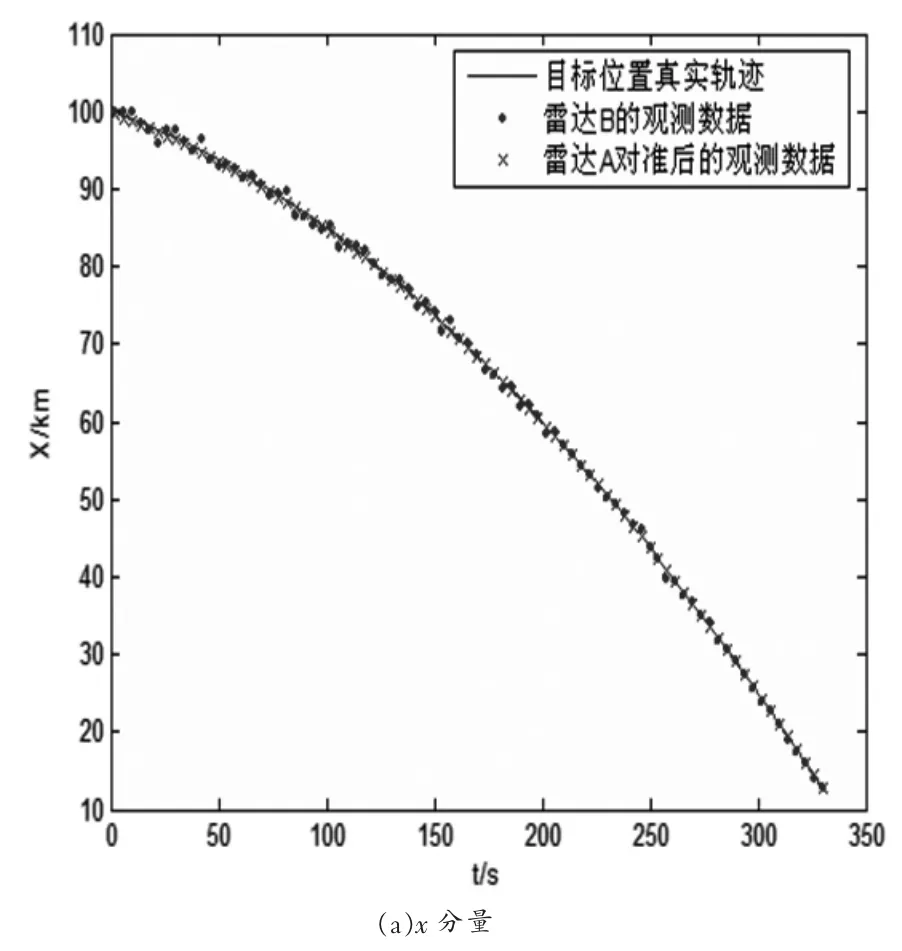
图2 对准后的观测数据

2.2 目标做匀速运动的情况

仿真条件与前面一节基本相同，所不同的是目标初始加速度为[0km/s2,0 km/s2,0 km/s2]。对准后的观测数据如图3所示，可以看出：对于目标做匀速运动的情况，基于抛物线拟合的时间对准方法同样能实现A、B两雷达观测数据的时间对准，且雷达A时间对准后的观测数据在精度上也得到了提高。

图3 对准后的观测数据

3 结论

从上面的仿真分析可以看出：对于雷达网内观测不同步的两部雷达，基于抛物线拟合的时间对准方法不仅适合于目标做匀加速运动的情况，而且适合于目标做匀速运动的情况。同时，该方法还使得对准后的观测数据更接近真实值，提高了观测数据的精度。

［1］杨万海.多传感器数据融合及其应用[M].西安：西安电子科技大学出版社,2004.

［2］王宝树,李芳社.基于数据融合技术的多目标跟踪算法研究[J].西安电子科技大学学报,1998,25(3)：269-272.

［3］韩崇昭,朱洪艳,段战胜,等.多源信息融合[M].北京：清华大学出版社,2006,4.