多维超几何分布协方差阵的简单求法①
2012-08-21 01:28:02吕宏啸
佳木斯大学学报(自然科学版) 2012年6期
吕宏啸
(吉林师范大学数学学院,吉林四平136000)
0 引言
在抽样调查中,经常遇到定性资料问题,设总体含有N个个体,考虑某一属性标志,共有A1,A2,…,Ak共K类属性,其中具有属性Ai的个体数为Mi,从总体中不放回地抽取容量为n的样本,若设具有各种属性的个体数分别为 X1,X2,…,Xk,则称(X1,X2,…,Xk)服从多维超几何分布,即
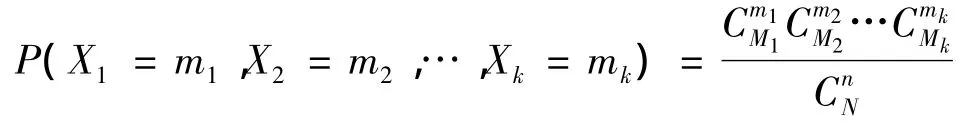
其中
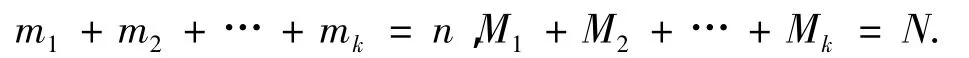
此时需要求出(X1,X2,…,Xk)的协方差阵,但以往的求法需要用到混合阶乘矩和有限差算子等不常用的概念和方法.本文利用初等的方法,非常简便地求出了多维超几何分布的协方差阵.
1 协方差阵的简单求法
引理1[1]若(X1,X2,…,Xk)是多维超几何分布,(Xi1,Xi2,…,Xik)是其中任意t(1≤t≤k)个分量,则(Xi1,Xi2,…,Xit)服从超几何分布.
引理2[2]Xi服从超几何分布,那么
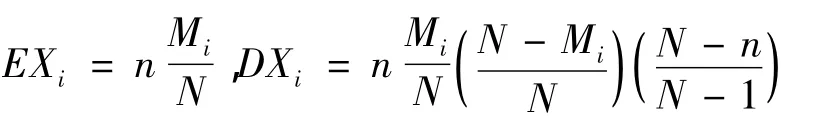
引理3 设随机向量(Xi,Xj)服从二维超几何分布,即
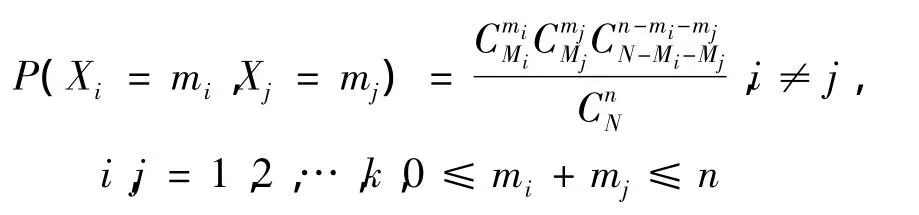
则
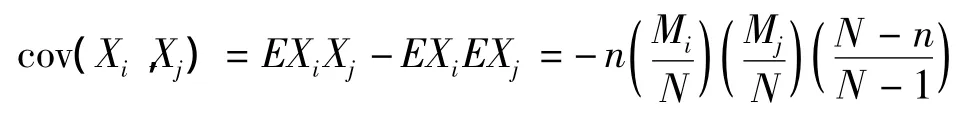
证明 不失一般性,取i=1,j=2,cov(X1,X2)EX1X2j-EX1EX2
其中
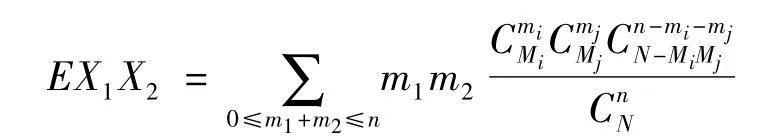
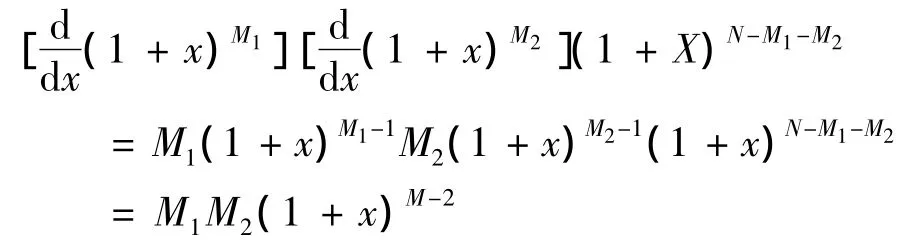
展开式中 Xn-2的系数,故从而
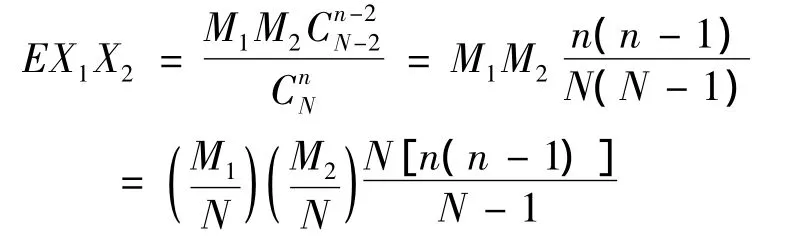
根据引理2,所以
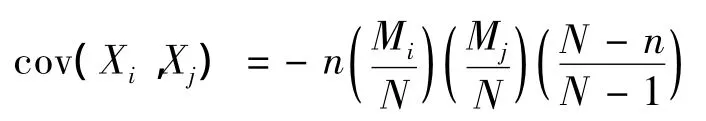
根据上述结论的引理2的证法,类似地可得到
定理1 多维超几何分布的协方差阵为
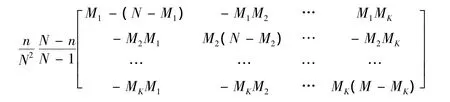
[1]方开泰,许建伦.统计分布[M].北京,科学出版社.1987:339-344.
[2]茆诗松,程依明,濮晓龙.概率论与数理统计教程(第二版)[M].北京:高等教育出版社,2011:101-102.
猜你喜欢
中学数学研究(2024年3期)2024-04-05 16:02:32
中学生数理化·高一版(2021年2期)2021-03-19 08:32:00
今日农业(2020年23期)2020-12-15 03:48:26
天府数学(2020年3期)2020-09-10 19:53:46
河北理科教学研究(2020年1期)2020-07-24 08:14:34
中国外汇(2019年6期)2019-07-13 05:44:06
中学生数理化·高一版(2017年2期)2017-04-25 13:22:36
数学学习与研究(2016年1期)2016-07-04 13:18:37
自动化学报(2016年8期)2016-04-16 03:38:55
无线电通信技术(2015年3期)2015-12-23 11:37:00

