贝塞尔函数在求解变系数微分方程的应用①
赵忠奎, 曹丽霞
(东北石油大学数学科学与技术学院,黑龙江大庆163318)
1 问题提出
在常微分方程中,关于二阶常系数线性微分方程的可解性及解的结构,有着详尽的讨论.而对于变系数的情形,除了几种特殊类型的方程以外,关于其解法的讨论尚不多见.现在,在常微分方程的研究中,虽然已经出现了许多引人注目的专题,但对于方程的解法的探讨,仍是十分重要的课题[1].
本文给出了一类二阶变系数线性微分方程,利用未知函数的线性变换转化虚宗量的贝塞尔方程来求解,其通解用虚宗量的贝塞尔函数表达式表示出来.
考虑如下二阶变系数线性微分方程
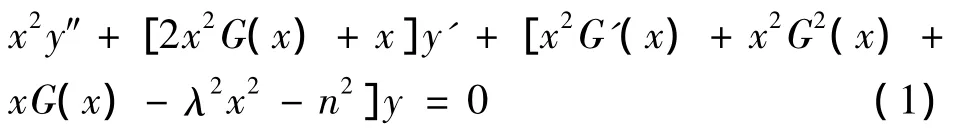
其中G(x)是已知可微函数,n为实数,λ为不等于零的实数.
2 方程求解
来求解方程(1),经适当未知函数的线性变换能化为虚宗量的贝塞尔方程.事实上,作变换[2]
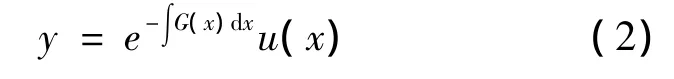
将函数y换成u
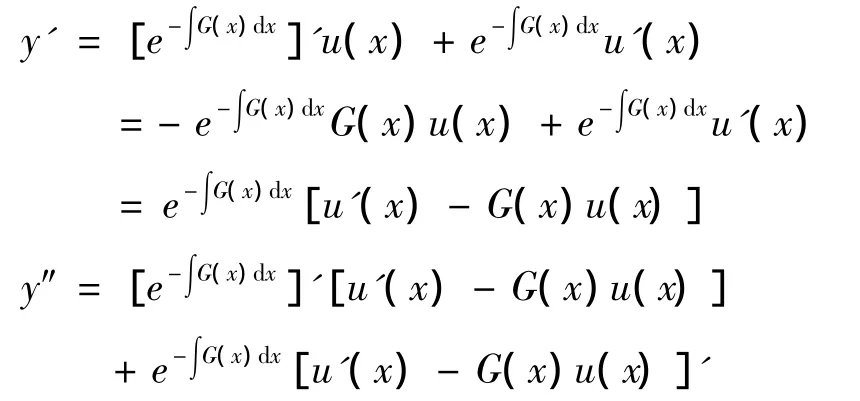
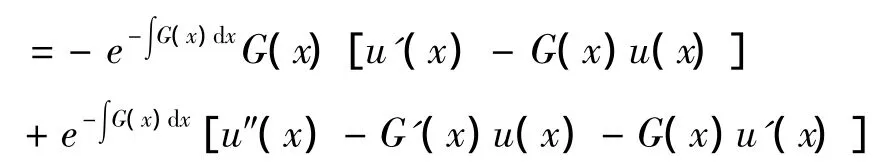
把它代入方程(1),便得到以u为未知函数二阶线性微分方程
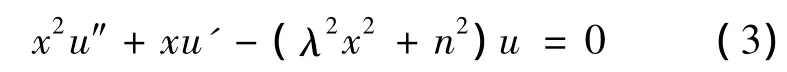
再作变换
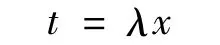
并记
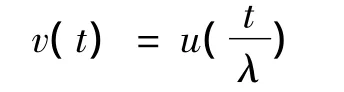
则得到

方程(4)是以v为未知函数虚宗量的贝塞尔方程[3]
从而,得到方程(4)的通解为
当n不为整数时,
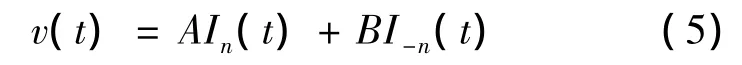
当n为整数时,
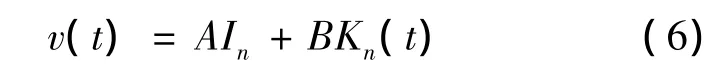
这里,In(t),I-n(t)为第一类虚宗量的贝塞尔函数,Kn(t)为第二类虚宗量的贝塞尔函数[4]
其中
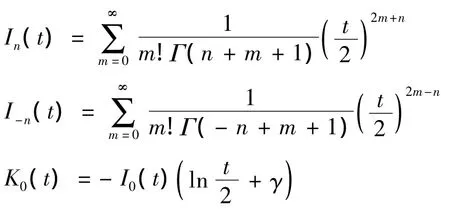
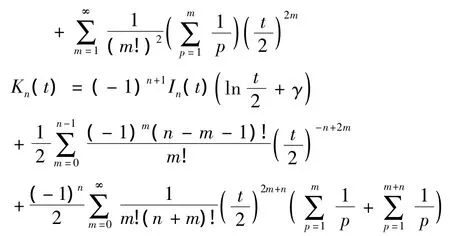
(n=1,2,3,…γ 为欧拉常数)
由(5)(6)式可得方程(3)的通解为
当n不为整数时
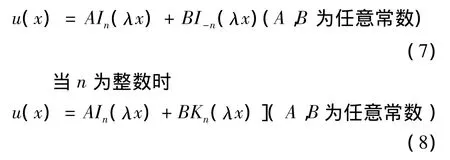
将(7)(8)式分别代入(2)式便得到微分方程(1)的通解为
当n不为整数时
当n为整数时
3 举例应用
下面举两个例子说明这种可解类型的应用
例1 解方程,
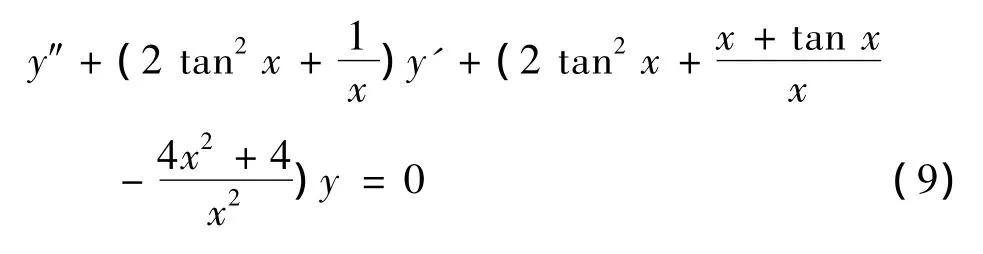
解 将方程变形成为
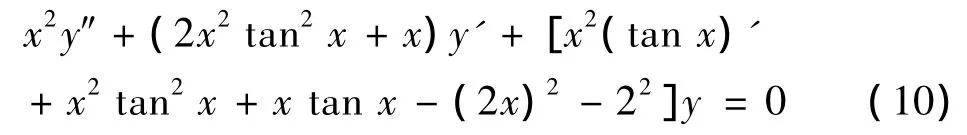
方程(10)便是方程(1)的类型,于是作变换
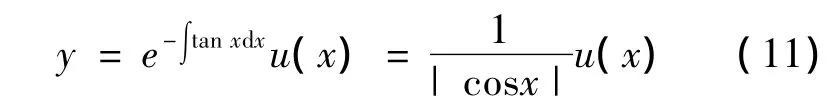
代入方程(10),得到
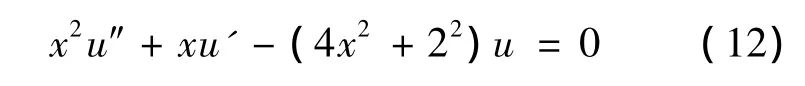
则得到
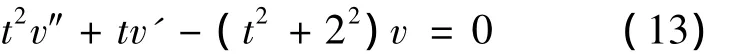
由于n=2为整数,根据(5)式得到方程(13)的通解为
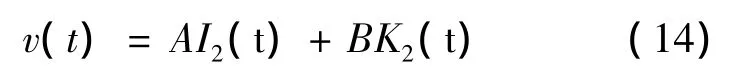
由(14)式得到方程(12)的通解
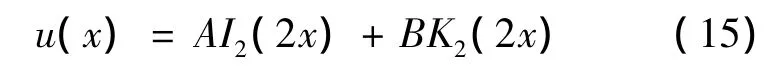
将(15)式代入(11)化简整理便得到原方程(9)的通解为
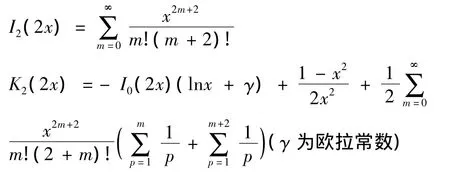
例2 解方程
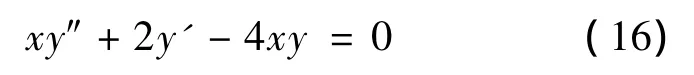
解 将方程变形为
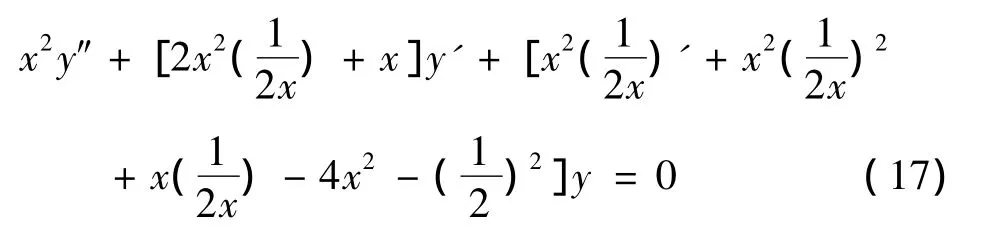
方程(17)便是方程(1)的类型,于是作变换
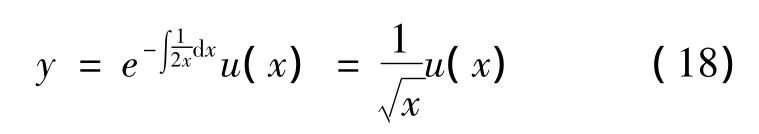
代入方程(17),得到
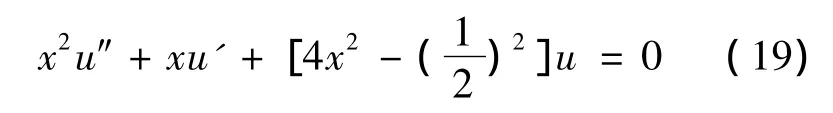
则得到
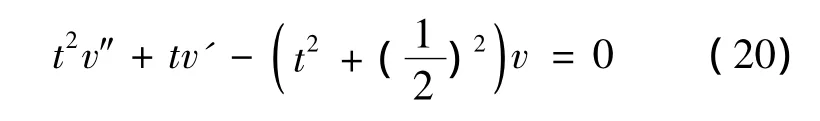
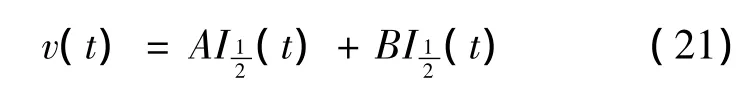
其中
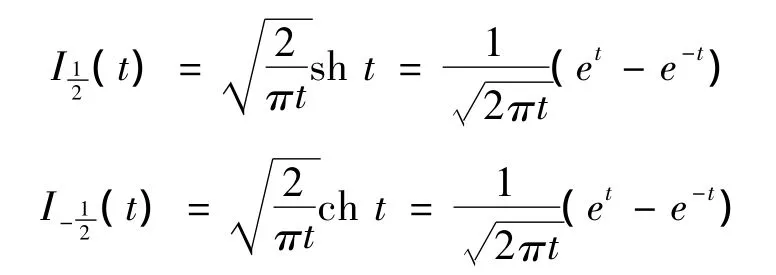
由(21)式得到方程(19)的通解
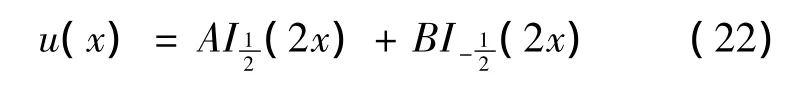
将(22)式代入(18)式化简整理后便得到原方程的通解为
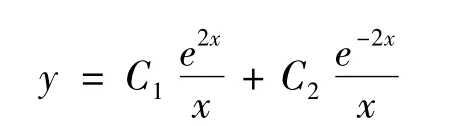
4 结束语
从上面的讨论和应用可以看出,根据虚宗量的贝塞尔函数的性质,当n为半奇数时,方程(1)的解为初等函数;当n不为半奇数时,方程(1)的解为用虚宗量的贝塞尔函数表达式表示出来的级数形式.
[1]王守田 关于二阶变系数线性常微分方程的转化问题[J].齐齐哈尔师范学院学报(自然科学版),2012,17(5):7-10.
[2]姬志飞 浅析二阶齐次线性变系数微分方程一个可积类型[J].应用数学与计算数学学报2006,20(1):125 -128.
[3]王元明.数学物理方程与特殊函数[M].北京:高等教育出版社,2004.1:130 -145.
[4]何淑芷.数学物理方法[M].广州:华南理式大学出版社,1994.8:251 -265.

