一类具有时滞和领导者的二阶离散多智能体系统一致性①
孟亚伟
(重庆师范大学数学学院,重庆401331)
0 引言
近年来,由于多智能体系统具有灵活性、鲁棒性和可扩展性,多智能体系统引起了专家学者广泛的关注,并已应用于多智能体编队控制[1]、传感器网络[2]等领域.“一致性”表示多个智能体状态达成一致,而这个达成一致依赖于所有智能体的状态.一致性是多智能体系统研究的一个重要研究部分.
多智能体系统离散时间一致性的研究目前结果不多.Vicsek等[3]提出了一种离散时间分布式模型,证明了该模型在群体密度足够大且噪声较小的情况下可以使多智能体达到一致.文献[4]中研究了一阶离散状态多智能体系统的一致性问题,得出了每个单智能体的状态趋于一致需要满足的必要或充分条件.Olfati等[5]提出并解决了一阶多智能体系统的一致性问题,并且研究了具有时滞的条件下一致性.文献[6]研究了一阶离散多智能体系统的一致性,给出了系统达到一致的矩阵不等式.文献[7]研究了在固定拓扑网络中一类多智能体系统的一致;文献[8]研究了在文献[7]中的控制下的系统在离散时间的一致性.
现实中大多工作关注多智能体系统无领导者或没有考虑时滞因素,在文献[8]中的控制协议基础上添加了时滞,本文针对具有领导者的二阶多智能体系统,研究了系统在离散时间一致性协议控制下的一致性.利用离散系统的稳定性理论分析系统的一致性,得到矩阵不等式,使得研究的系统达到一致性.
1 模型描述及预备知识
考虑n+1个智能体,其中智能体r被称之为领导者,其余的智能体作为跟随者跟随领导者运动即每个跟随者的行为都受领导者的状态影响,智能体可以描述为1,2,…,n.领导者是独立的,其它的智能体之间有一定的联系,位置和速度的变换相互影响.假设每个智能体都是有向图G的一个节点.因此可以用图G来描述智能体之间的信息交互关系.有向图G=(V,E,A)由一个有限结点集合 V={1,2,…,n},一个有向边的集合和E⊆V×V权重矩阵A所构成.eij=(i,j)∈E叫做边,i称为边的起点,j称为边的终点,边的方向从i指向j,连接权值矩阵为 A= [aij],对于 ∀i∈ I,aii=0,当 i≠ j,aij= eij> 0.D = diag{deg(1),deg(2),…,deg(n)},D称为G的度矩阵.
对于二阶离散时间的多智能体一致性系统可表示为
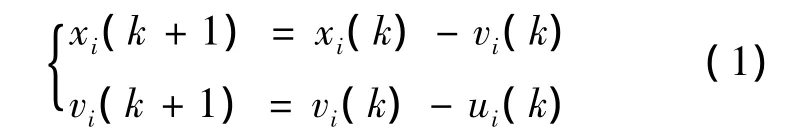
其中k=1,2,…,n,xi(k)表示第i个智能体在时刻k的位置;vi(t)表示是第i个智能体在时刻k的速度;ui表示系统的控制输入.
对于领导者的动力系统为
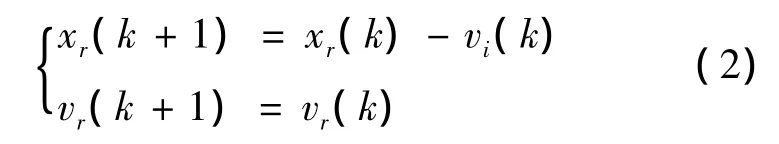
智能体之间的系统控制可以描述为
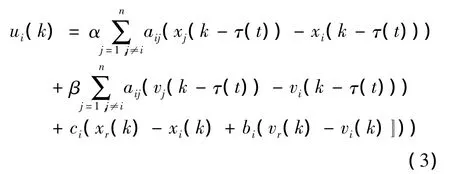
式中:α > 0,β > 0,0≤ τ(t)≤ τ,τ是一个非负的常数.τ(t)是时变时延,智能体与领导者之间的连接元素ci(i∈I),ci=air(i∈I).如果智能体与领导者没有获得相关信息,那么,ci=0若智能体与领导者之间有信息的传递则ci>0.
定义 假定带有领导者的多智能体系统,对于智能体的状态 xi,vi,当,则多智能体系统达到一致.
2 主要结果
对于在控制(2)下的多智能体系统(1)可以重写为
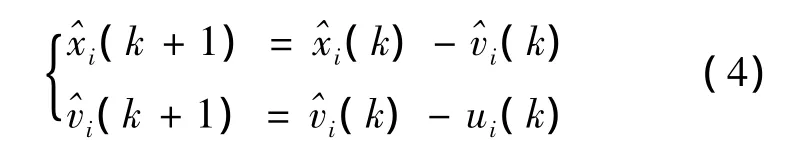
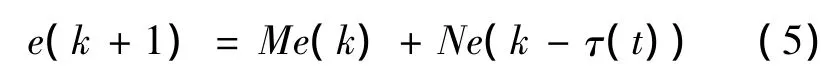
在固定拓扑网络中,系统(1)在控制(3)的情况下,
定理1 多智能体系统(1)达到一致的充分条件是对于矩阵
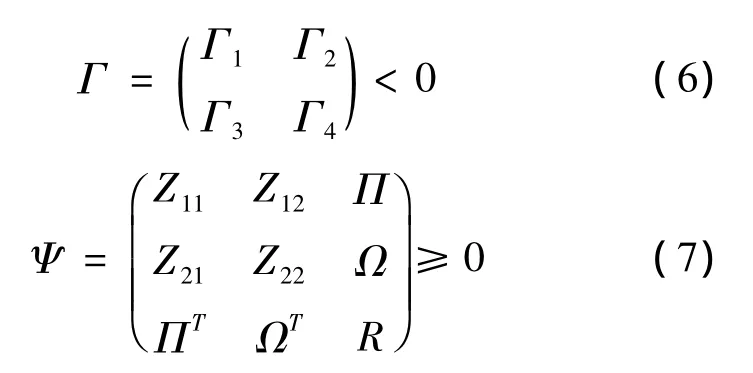
式中,
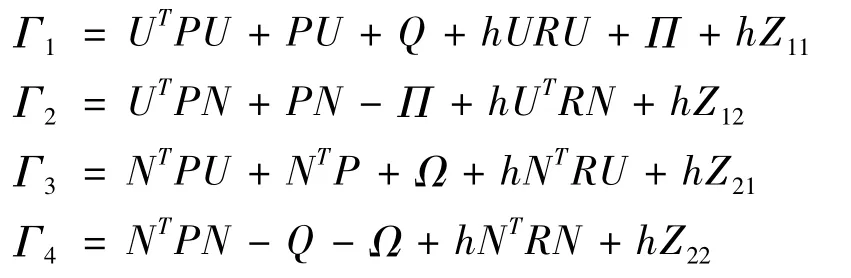
证明构造Lyapuouov函数
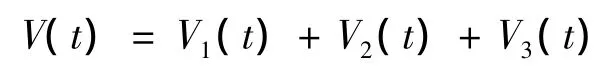
其中V1(t)=eT(t)Pe(t)
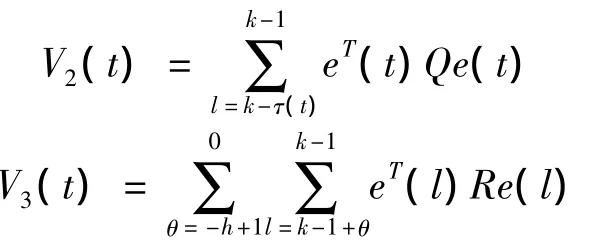
定义差分方程
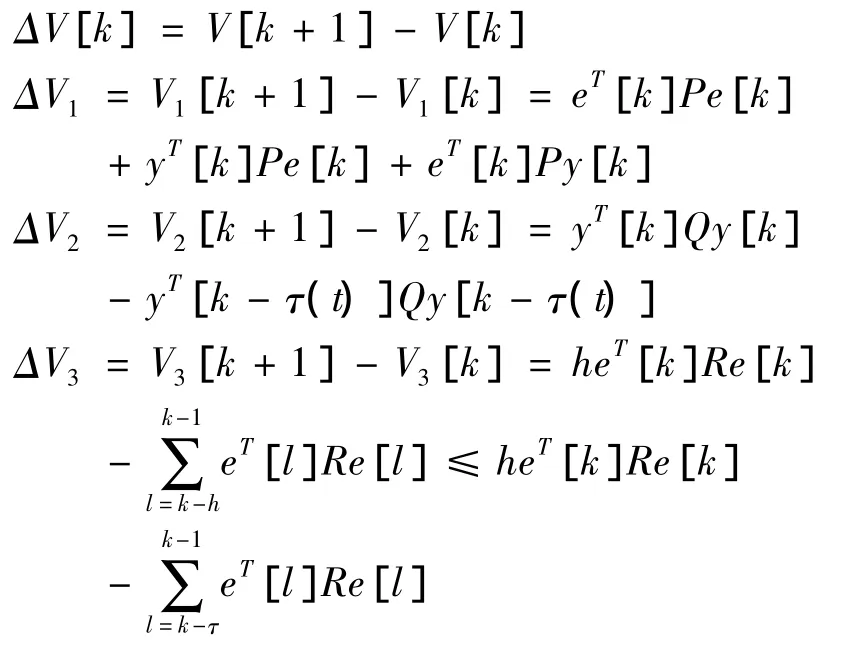
其中 e[k]=y[k]- y[k - 1]
则有
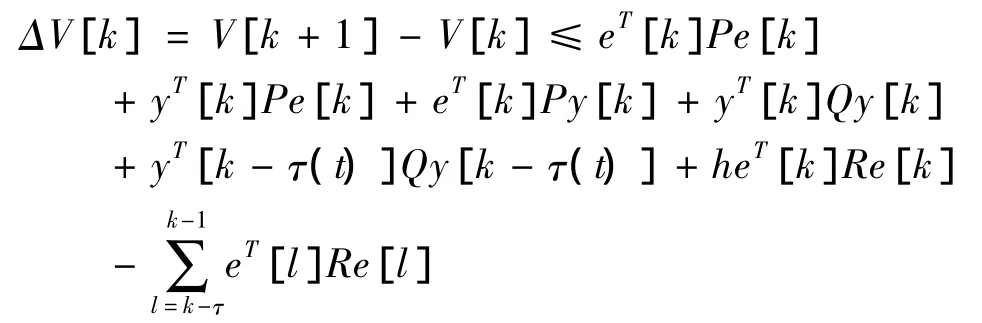
上式可以变换为
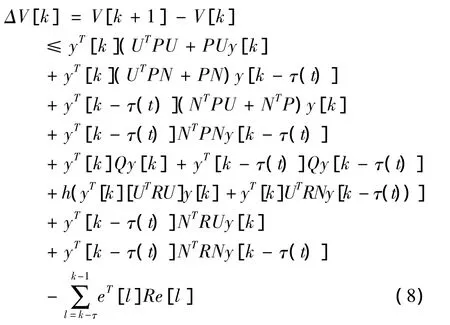
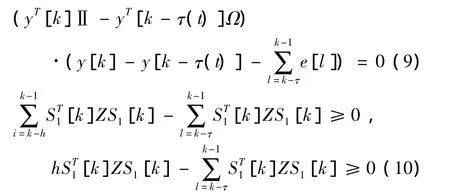
将式(9)和(10)加入式(8)中得到
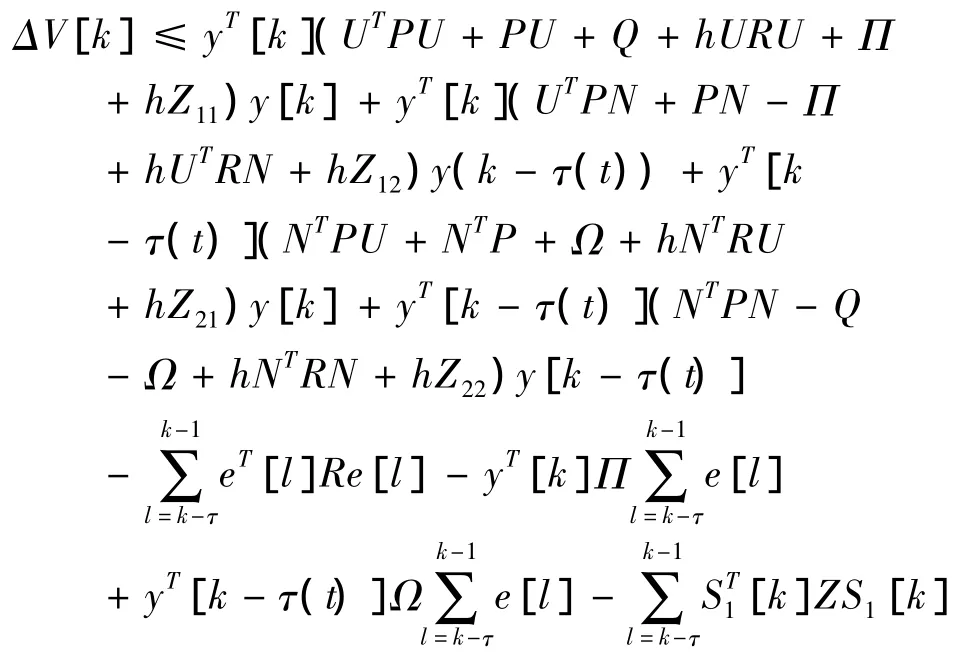
当系统(1)满足矩阵不等式(6),(7)时,V是正定的,ΔV是负定的,根据Lyapunov稳定性定理,系统(1)是渐近稳定的,多智能体系统(1)达到一致.
3 结论
本文主要运用矩阵不等式得到具有时滞和领导者的二阶离散多智能体系统(1)最终达到一致的充分条件,得到的结果有待于进一步简化,系统考虑的时滞是相同的,对于当系统中每个智能体所考虑不同时滞的研究还需要进一步研究.
[1]俞辉,王勇骥,程磊.稳定的有领航者的多移动agengt群集运动控制[J].华中科技大学学报:自然科学版,2005,33(8):56-58.
[2]StankovicSS,Stankovic M S,Stipanovic DM.Consensus based over Lapping Decentralized Estimation with Missing Observations and Communication Faults[C].Proceedings of the World Congress and The International Federation of Automatic Control,Seoul:Springer,2008:9338 - 934.
[3]Vicsek T,,Czirok A,Schochet O.Novel Type of Phase Transitions in a System of Self - Driven Particles[J].Phys.Rev.Lett.,1995,75:1226 -1229.
[4]Moreau L.Stability of Multi-Agent Systemswith Time Dependent Communication Links[J].IEEE Transactions on Automatic Control,2005,50(2):169 -182.
[5]杨亚桥,吴晓峰,林茜.多智能体离散时间一致性跟踪研究[J].华中科技大学学报:自然科学版,2011,39(10):69 -72.
[6]Jadbabaie,A,Lin,J,Morse S.A.Cooedination of Groups of Mobile Agents Using Nearest ighborrules[J].IEEE Transactions on Automatic Control,2003,48(6):988 -1001.
[7]W.Yu,G.Chen,M.Cao,etc.Second-order Consensus for Multi-Agent Systems with Directed Topologies and Nonlinear Dynamics[J].IEEE Trans.SystMan Cybern.Part B,2010,40(3):881-891.
[8]DongmeiXie,ShaokunWang.Consensus of Second - Order Discrete-Time Multi- Agent Systems with Fixed Topology[J].Journal of Mathematical Analysis and Applications,2012(387):8-16.

