基于MFC和OpenGL的地质模拟①

赵 坡， 白 林， 刘大宁， 杨永乐

(成都理工大学信息管理学院数学地质四川省重点实验室，四川成都610059)

0 引言

随着现代社会的发展，特别是城市的快速发展，使得人类对城市的依赖程度愈来愈大，在城市建设过程中，所要考虑的问题也越来越多样化、细致化，诸如城市地下水排水系统、电缆铺设管道总体布局等也越来越复杂化.如何使施工成本降低，避免不必要的施工事故，预测施工效果，已成为城市建设的重点，这就要求我们可以通过城市三维地质建模的方法，构造城市地下分布结构模型.本文以城市三维地层模拟为研究点，主要介绍了基于MFC和OpenGL的有关城市地质模拟的应用，重点介绍了反距离权重插值原理，并用它进行了具体实现.

1 MFC和OpenGL的技术结合

OpenGL主要应用于三维图形显示，是一种开放的软件包，具有很好的可移植性，可以十分方便地在各平台移植［1－2］.而 Visual C++ 可以与OpenGL紧密结合，再加上其良好的封装性，可以保证算法的准确性和可靠性.

MFC作为Visual C++的基本类型库，包含了强大的基于Windows的应用框架，并且包含了大量的窗口和事件函数，日益成为了比较流行的工作平台.在三维建模方面，OpenGL和MFC相结合已逐渐成为一种主流趋势.

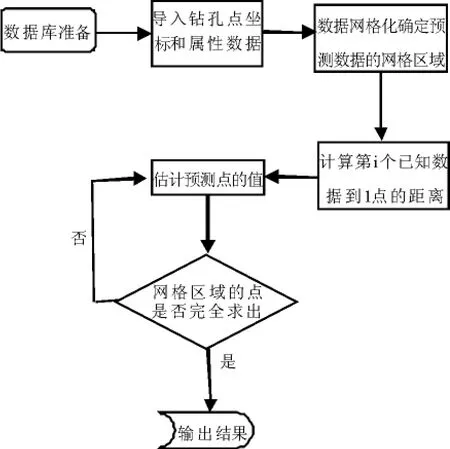
图1 反距离权重插值流程图

2 反距离权重插值流程

如表所示，首先就是导入钻孔点的坐标和属性数据，通过利用网格化确定所研究范围，计算第个已知点数据到1点的距离，利用IDW插值算法根据数据属性的相关性继而估算出预测点的数据信息，在这一过程中可能有些点没有求出，要做一个判断，是否所有点都已求出，如果否，则重复上一步，否则输出结果.

3 反距离权重(IDW)插值原理

IDW插值算法是基于Tobler定理提出的插值方法.主要是根据空间中越靠近的事物其现象或属性就越接近，由待测点周围的各点的测量值的加权平均数进行插值，距离待测点越近，其权系数就越大.所以，IDW在附近范围内插值，对其周围空间位置有着较强的依赖性.

图2 OpenGL显示效果图

图3 地层的OpenGL 3D效果显示图

一般表达式为:

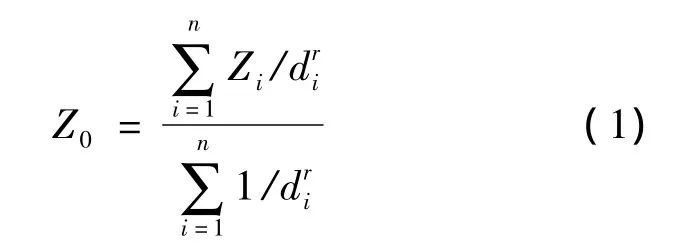
式中，Z0为0点的估计值;Zi为控制点i的Z值;di为控制点i与点0间的距离;n为在估算中用到的控制点数目，r为指定点的幂数.

对于公式(1)，取r=1进行分析，将1/dr作为离散型的取值，则

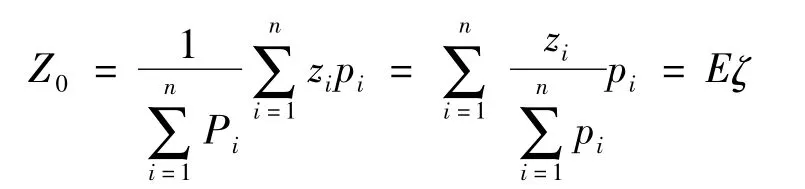
可见加权平均就是期望，此时Z0取值的概率为加权平均的方差为:

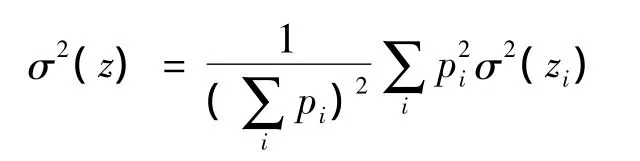
由 piσ2(zi)= σ2得:

根据pi权与标准差σi的关系式:

标准差越小，权越大.如果标准差平方σ2的测量权p=1，则标准差平方为的测量的权pi为:

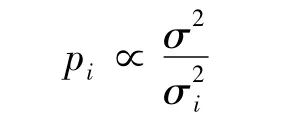
从而可以看出标准差的大小，直接由权值影响，所以决定了插值整体精度情况，对插值结果影响很大.

4 利用反距离权重插值原理实现有关三维地质建模中的实际应用

4.1 数据来源

所选数据是某城市钻井数据，包括29个钻井，表1是其中的部分数据，横坐标、纵坐标分别是经过处理过后的钻井坐标，顶深1、顶深2、顶深3、顶深4、顶深5分别是根据地层岩性进行的分层，所代表的数值是相对海平面的值，所选区域具有代表性.可以体现三维城市建模的实际意义.图2是钻孔的OpenGL显示效果图.

表2是原始数据经过变换的反距离权重插值原理(IDW)插值后的部分分层网格点坐标数据，第一列和第二列分别代表x、y坐标，第三列各代表岩层相对海平面位置，在这里都经过了处理，方便以后OpenGL显示效果更加明显.

4.2 效果显示

图3是地层的OpenGL 3D效果显示图，由已知数据的岩性知道该数据能分成5层，在这里分别用不同的颜色区分，可以直观地看出钻井的实际分层情况，该图地层分布基本符合该区地层实际状况，从而，通过利用反距离权重原理进行数据处理，再利用OpenGL在三维显示方面的优势，两者的有机结合，能够在地质模拟方面达到满意的三维图形 显示效果.

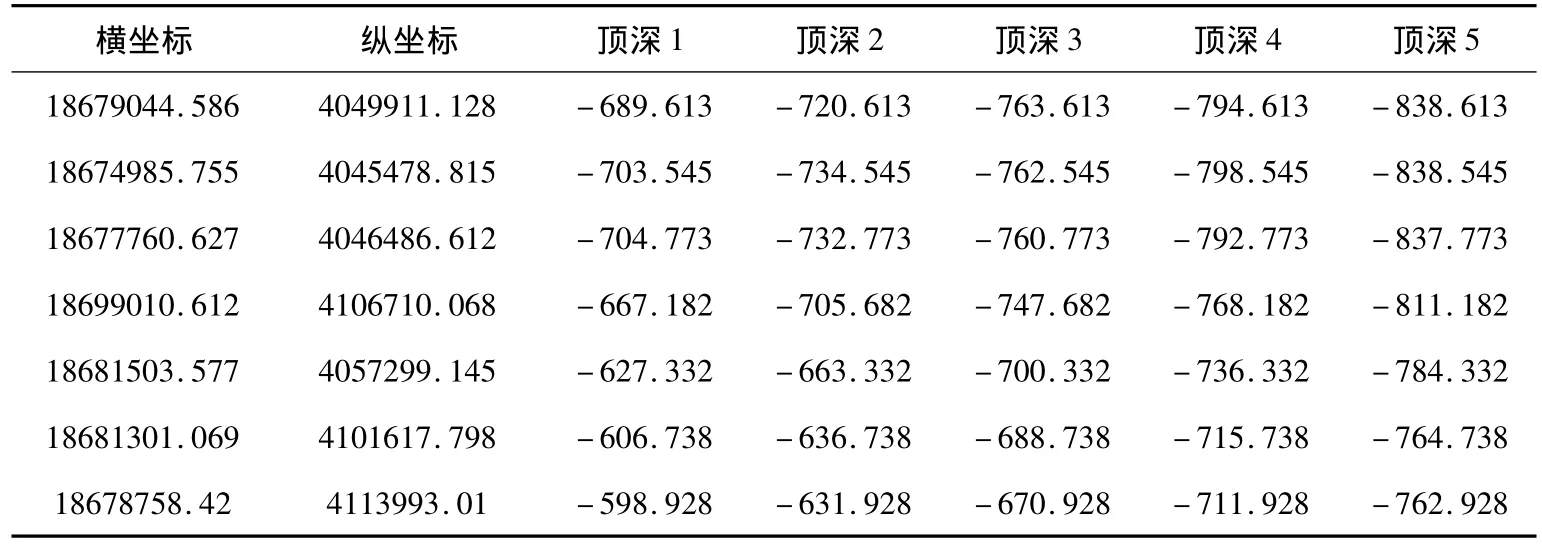
表1 钻孔数据(单位:m)

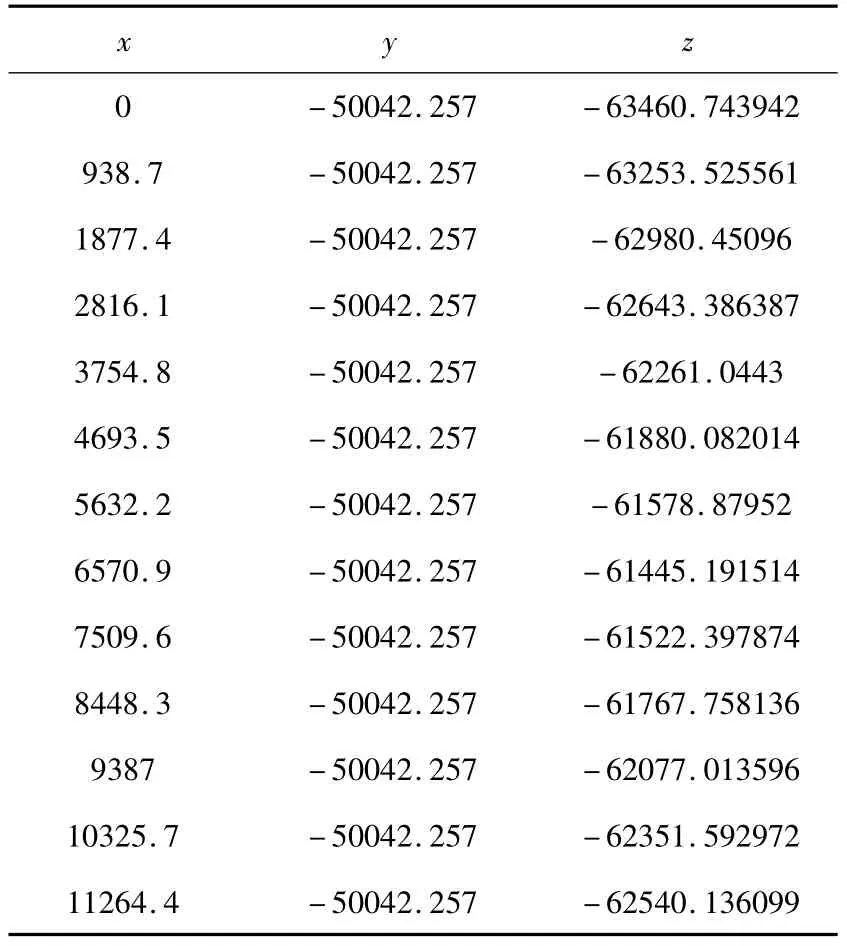
表2 IDW插值结果(单位:m)

5 结束语

本文着重介绍了基于MFC和OpenGL的地质模拟，其中详细介绍了反距离权重插值原理，并用其对已知数据进行了插值演算，得到了对应的网格坐标，并利用OpenGL对其进行了三维显示，所得结果基本与实际情况符合，能直观地反映该地区地层分布状况，从而达到了预期效果.

［1］李军，徐波，等译.OpenGL Programming Guide［M］.北京:机械工业出版社2010.3.

［2］候俊杰.深入浅出MFC第二版［M］.武汉:华中科技大学出版社 2010.4.

［3］孙鑫，余安萍.Visual C++深入详解［M］.北京:电子工业出版社 2006.06.

［4］和平鸽工作室编著.OpenGL高级编程与可视化系统开发高级编程篇［M］.北京:中国水利水电出版社2006.

［5］Zhu William.Relationship among Basic Concepts in Coveringbased Rough Sets［J］.In － formation Sciences，2009，179:2478－2486.