人工冻土解冻温度场数值分析
龚 旭
(镇江新区建设工程质量中心,江苏镇江 212000)
0 引言
随着社会经济的发展,国内许多大中城市出现了地面交通拥堵及城市用地的危机。地铁作为一种快捷便利的地下交通运输工具在解决交通拥堵问题的过程中具有重要作用。然而地铁在建造过程中也存在着一定的风险,主要是在盾构到达过程中洞门后土体稳定的问题。因此需对盾构到达或始发区域内洞门土体作一定的加固。冻结法作为一种形式灵活、适应性强、施工无污染、对环境影响小的土体加固方法在盾构进出洞施工应用中具有广阔的发展前景。关于冻结地层加固技术在城市隧道建设中的应用已经获得了一些有益的施工经验[1-6]。
本文根据某车站盾构到达人工水平冻结加固工程为例,运用数值计算对此展开理论研究,并据此为类似工程提供借鉴。
1 工程概况
1.1 工程、水文地质
根据详勘报告,盾构到达施工场地内工程、水文地质较为复杂,且地下水具有承压性,地下水与秦淮河及长江均存在水力联系。
场地内土层自上而下依次为:杂填土(①-1)、粉质粘土()、淤泥质粉质粘土)、粉砂()、粉土()以及粉砂)。
1.2 盾构到达加固方案
盾构机外径为6.34 m,为保证盾构机到达过程中洞门范围内土层的稳定性和周边建筑物、管线的安全,采用三圈冻结管的加固方案,最终形成水平杯状冻结壁,防止盾构到达过程中水土涌入车站北端头的盾构井内,如图1所示。
2 自然解冻数值分析
2.1 计算模型
盾构到达后,仅留下最外层1.8 m厚冻土帷幕,其自然解冻数学模型如图2所示。

图1 冻结管布置图
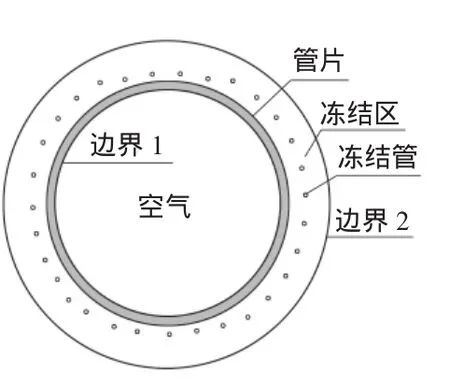
图2 数学模型图
边界2存在着未冻土与冻土间的三维热传导,其数学表达式:

其中,Ti为冻土中温度,i=s时为冻结区温度,i=l时为未冻区温度;αi为导温系数,i=s,l。
边界1存在着隧道内的空气与混凝土管片之间的热对流:

其中,q为热流密度,W/m;h为表面对流换热系数,W/(m·K);ts为边界温度;tf为温度在边界面上的给定值。
管片内热传导方程同式(1),当通过热传导后管片与冻土壁交界面处温度达到解冻温度后,相变就开始自边界1以环状向四周扩展,在相变界面上有:

其中,X(t)为相界面位置;Tf为冻结温度;L为相变潜热;Ks,Kl分别为固相区和液相区导热系数;Ts,Tl分别为固相区和液相区温度。
2.2 计算参数
计算参数见表1。

表1 材料参数表
2.3 有限元模型
三维有限元模型采用8结点单元,对洞门附近进行网格细分处理,冻结过程计算60 d,自然解冻计算120 d。三维有限元模型见图3。
3 计算结果分析
由冻结计算结果可以看出,盾构达到后在洞门上方形成了3 m长的水平冻土帷幕,在洞门下方形成了6 m长的水平冻土帷幕,如图4所示。将该温度场作为自然解冻温度场初始条件进行进一步分析。
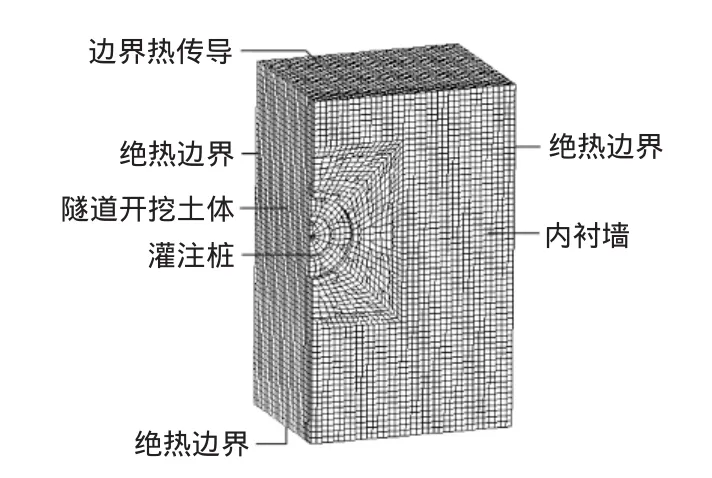
图3 盾构到达水平冻结加固有限元模型
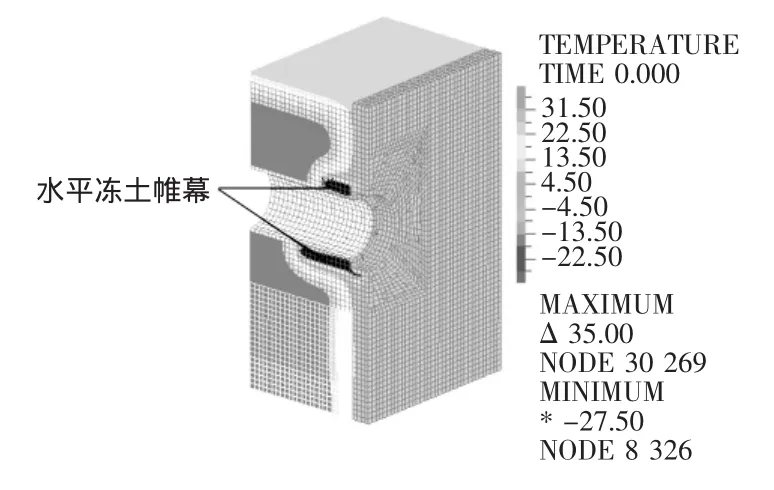
图4 盾构到达后水平冻结温度场
3.1 与实测数据对比
为确保工程的安全性,在进行数值计算的同时,笔者也对洞门处冻结与自然解冻温度场进行了全场监控量测,将处于相同位置的实测与计算结果进行对比,如图5所示,两者基本吻合。说明所提出的数学模型和采用的数值计算模型是合理可行的。

图5 计算值与实测值对比曲线图
3.2 冻土帷幕自然解冻时间分析
根据自然解冻0℃等值线图判断,3 m长的水平冻土帷幕自然解冻时间为40 d左右,6 m长的水平冻土帷幕自然解冻时间为60 d左右。
3.3 冻土帷幕自然解冻速率分析
自然解冻过程中相变界面位置及解冻锋面推进速率曲线如图6,图7所示。
由图6,图7可以看出,随着停止冻结后自然解冻时间的延长,解冻速率逐渐减缓。这主要是由于解冻前期,冻土壁内温度梯度较大导致热传导较为迅速,而解冻后期随着冻土壁内温度梯度的减小,热量传导也随之减缓引起的。

图6 相界面距离轴面随时间关系曲线

图7 解冻速率随时间关系曲线
4 结语
通过对有限元数值计算结果的分析和与实测结果的对比,得到以下几点结论:
1)盾构到达水平冻结加固形成的冻土帷幕自然解冻时间约为60 d。
2)人工冻结壁自然解冻速率随着解冻时间的增加而减慢。
3)影响盾构达到人工水平冻土帷幕自然解冻的主要因素为隧道空气散热及未冻土的热传导。
[1]Ping Yang,Jie-ming Ke,J.G.Wang,et al.Numerical simulation of frost heave with coupled water freezing,temperature and stress fields in tunnel excavation[J].Computers and Geotechnics,2006(33):6-7.
[2]翁家杰.井巷特殊施工[M].北京:煤炭工业出版社,1991.
[3]白 楠.人工冻土强制解冻融沉控制研究[D].上海:同济大学土木工程学院,2008.
[4]Kunieda T,Sato T,Ido S.Numerical case studies of ground freezing for the construction of drain pump chambers[J].Ground Freezing91.Rotterdam:Balkema,1991(13):97-99.
[5]李述训,吴通华.冻土温度状况研究方法和应用分析[J].冰川冻土,2004,26(4):112-113.
[6]纳斯诺夫,苏普力克.立井冻结壁形成规律[M].陈文豹,伍期建,梁惠生,译.北京:煤炭工业出版社,1981.

