FSAE赛车弯道竞赛动态转向特性研究

倪 俊

(北京理工大学机械与车辆学院，北京 100081)

国内关于赛车动力学的研究还处于起步阶段[1]，数据积累和理论分析都很匮乏.所以，有必要对赛车动力学进行基础研究[2-3].

对于民用车而言，其瞬态响应及稳态响应特性往往是在恒定车速的条件下进行评价的.但对于赛车而言，为了提高赛车的圈速往往在入弯前减速、出弯时加速，由于纵向加速度的变化会造成前、后轴载荷的转移，从而影响到前、后轮的侧偏刚度，进而影响赛车的转向特性.以此为依据，通过对比赛中所采集的加速度数据进行分析，在瞬态和稳态响应的分析中综合考虑了轴荷分配对轮胎侧偏刚度的影响.

1 二自由度模型与传递函数

在汽车操纵特性的分析中，主要应用的是角输入二自由度、考虑侧倾的三自由度等模型，虽然随着虚拟样机和数值仿真技术的发展，更高自由度的汽车模型已经得到广泛应用，但低自由度模型反映了汽车最基本的运动和操纵特性，并且由于赛车侧倾并不明显，所以采用二自由度角输入模型对其进行操纵特性分析，其示意图如图1所示，公式具体推导过程可见文献 [4].

图1 二自由度汽车模型

二自由度汽车运动微分方程如下

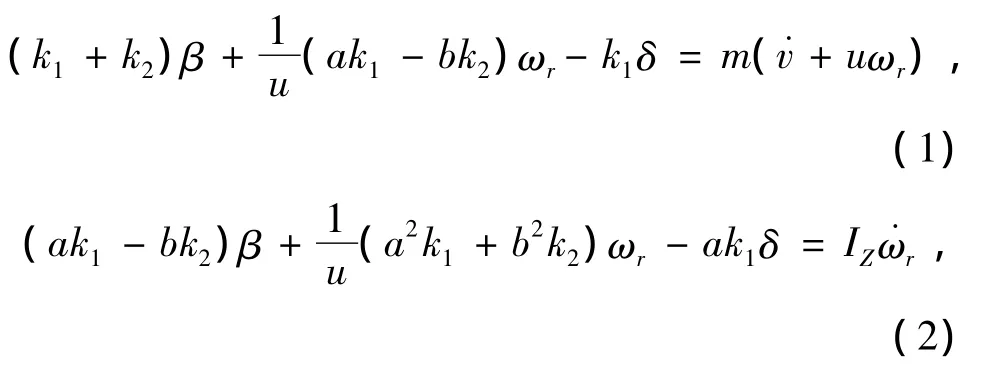
式中:k1、k2为前后轮侧偏刚度;a、b为质心距前、后轮的距离;m为整车质量;u为沿纵轴速度;v为沿横轴速度;β为质心处侧偏角;δ为前轮转角;ωr为横摆角速度;α1、α2为前后轮侧偏角;F1、F2为前后轮侧向力;L为汽车轴距.

考虑前轮角阶跃输入，经计算及简化后可得与单自由度强迫振动微分方程形式相同的运动方程

式中:ω0称为固有圆频率;ζ称为阻尼比;B0为与结构参数有关的常数.其具体表达式如下

同时在文献[4]中定义了所谓稳定性因数用于表征汽车稳态响应

当K=0时为中性转向;K＞0时为不足转向;K＜0时为过度转向.

对式 (1)进行拉氏变换，可得

以前轮转角作为输入，横摆角速度为输出，可得二者间传递函数

2 轴荷转移对轮胎侧偏刚度的影响

2.1 入弯和出弯时的纵向加速度

因为赛车质心较低且悬架侧倾角刚度较大，所以只考虑赛车纵向轴荷的转移.从车载信息系统中截取某单圈赛车纵向加速度和速度的变化曲线，如图2和图3所示.所统计的赛车在各弯道时的车速和加速度变化如表1所示.

图2 某单圈纵向加速度曲线

图3 某单圈速度曲线

表1 赛道弯道数据统计

2.2 轴荷转移

以赛车具有负的纵向加速度为例，其轴荷转移如图4所示.

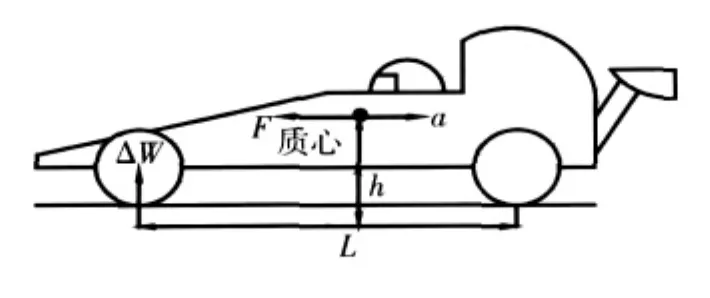
图4 轴荷转移示意图

图4中，h为质心距地面距离;L为赛车轴距;a为纵向加速度;F为加速度产生的惯性力;ΔW为前轮产生的附加轴荷.研究中，以第5弯道为例.

通过对后轮的力矩平衡关系，即可求出此时前轮附加轴荷.如式 (10)所示

当赛车具有正的纵向加速度时，后轮附加轴荷的求法与此相同.

由2.1节可知，在第5弯道入弯时，加速度为－0.5 g，出弯时加速度为0.7 g，赛车的主要结构参数如表2所示.

根据公式 (10)可计算得赛车入弯时的前、后轴负荷分别为1 327 N、1 173 N，出弯时的前、后轴负荷分别为765 N、1 735 N.

根据赛车所采用18×6－10型Hoosier轮胎试验数据可推算知赛车入弯和出弯时的轮胎侧偏刚度，如表3所示.同时，当赛车不存在轴荷转移时，前后轮侧偏刚度分别为16 000 N/rad，17 900 N/rad.

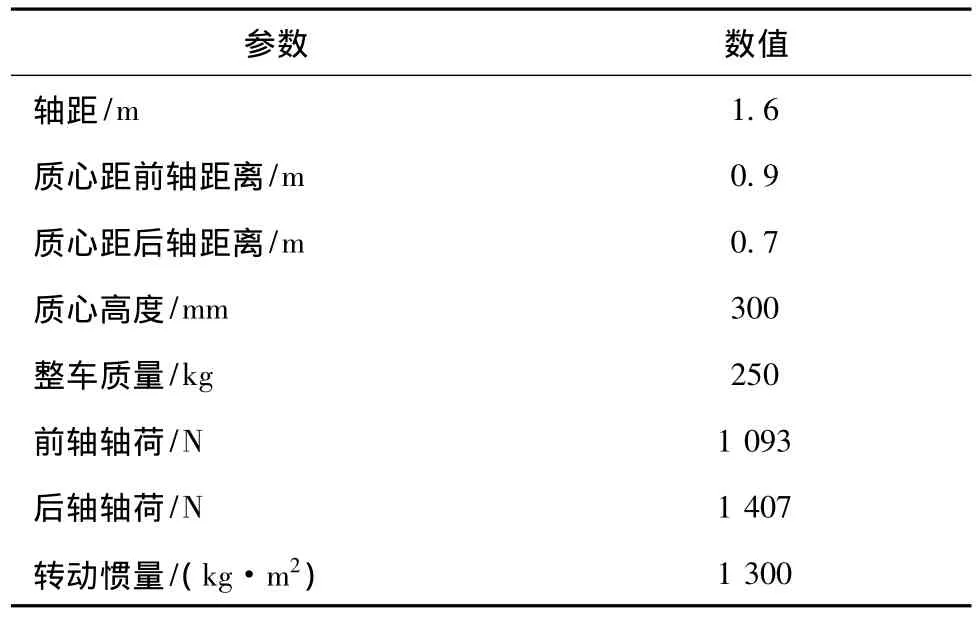
表2 赛车主要参数

表3 赛车入弯、出弯时轮胎侧偏刚度

3 赛车瞬态和稳态响应分析

3.1 不计入轴荷转移赛车入弯及出弯

假设赛车在入弯及出弯时，不发生轴荷转移，在第5弯道入弯速度为45 km/h，出弯速度为60 km/h，转向盘输入阶跃信号后赛车的横摆角速度响应如图5所示 (注:计入轴荷转移简称“计”，不计入轴荷转移简称“不计”).

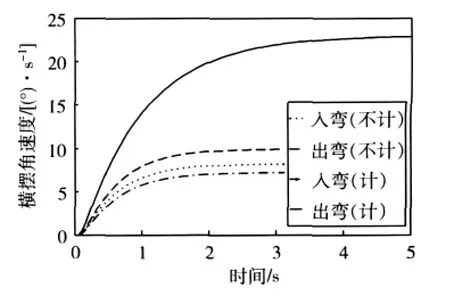
图5 赛车入弯与出弯时横摆角速度响应

同时由公式 (7)可知，此时赛车转向稳定性因数K=6.4×10－4，赛车接近中性转向.不计入轴荷转移时，赛车入弯时的横摆角速度增益约为7.5，出弯时横摆角速度增益约为9.赛车为阻尼比大于1的无超调系统.

3.2 计入轴荷转移赛车入弯

计入轴荷转移.将表2与表3的数据代入公式 (9)中，可得赛车入弯时横摆角速度与前轮转角间传递函数，入弯时速度为45 km/h，令转向盘输入阶跃信号，横摆角速度时域响应如图5所示.

此时赛车固有圆频率ω0为3.67 rad/s，阻尼比ζ为1.41，可见，此时赛车仍为一个阻尼比大于1的无超调系统，此时横摆角速度增益约为7.与不计入轴荷转移相比，入弯时的轴荷转移造成了赛车的横摆角速度增益减小.

由计算可知赛车入弯时K=0.001 2 s2/m2为明显不足转向.

3.3 计入轴荷转移赛车出弯

出弯时速度为60 km/h.令转向盘输入阶跃信号，横摆角速度响应如图5所示.

根据公式 (7)可知，赛车出弯时 K=－0.001 2 s2/m2，即为过度转向.此时赛车固有频率ω0为1.84 rad/s，阻尼比ζ为2.23，此时赛车仍为一个阻尼比大于1的无超调系统，由系统理论知[5]，当二阶过阻尼系统的阻尼比增大的时候，其调节时间增大，响应速度减慢.此时横摆角速度增益约为22.8，且响应时间增大.

可见，出弯时的轴荷转移使赛车从接近中性转向变为了过度转向.

4 其他主要结构参数的影响

4.1 轴距的影响

在赛车设计时，轴距是可以在规则限定的范围内自由制定的.赛车原轴距为1.6 m，分别将轴距增大和减小为1.8 m和1.4 m.并假设赛车的其他结构参数不变.轴距变化后赛车在入弯时的横摆角速度响应如图6所示.

图6 入弯时不同轴距横摆角速度响应对比

赛车轴距为1.8 m时，ω0为3.18 rad/s，阻尼比ζ为1.24.赛车轴距为1.4 m时，ω0为2.88 rad/s，阻尼比ζ为1.58.

由图6可见，若将轴距增大为1.8 m，横摆角速度增益减小，则增大了入弯时的不足转向，若将轴距减小为1.4 m，则减小了不足转向.

轴距变化后赛车在出弯时的横摆角速度响应如图7所示.

图7 出弯时不同轴距横摆角速度响应对比

由公式 (10)知，改变轴距后，赛车出弯时仍为过度转向.

赛车轴距为 1.8 m时，固有圆频率 ω0为2.42 rad/s，阻尼比ζ为1.82.赛车轴距为1.4 m时，ω0为1.38 rad/s，阻尼比ζ为2.77.

由图7可见，若将轴距增大为1.8 m，横摆角速度增益减小，则减弱了出弯时的过度转向，若将轴距减小为1.4 m，则增大了过度转向.

4.2 转动惯量的影响

在赛车设计之初，通常根据赛车的三维装配模型粗略估计赛车绕垂直于地面轴线的转动惯量，所以，有必要对赛车转动惯量的变化对操纵特性的影响进行分析.

赛车原转动惯量为1 300 kg·m2，分别将其增大和减小为1 600 kg·m2和1 000 kg·m2.并假设其他结构参数不变.则赛车入弯时横摆角速度响应如图8所示.

图8 入弯时横摆角速度响应对比

赛车转动惯量为1 600 kg·m2时，固有频率为ω0为2.9 rad/s，阻尼比ζ为1.50.赛车转动惯量为1 000 kg·m2，固有频率为ω0为3.29 rad/s，阻尼比ζ为1.25.由图8可见，增大或减小转动惯量对转向特性的影响很小.减小转动惯量可以小程度提高响应速度，但效果并不显著.

赛车出弯时不同转动惯量的横摆角速度响应如图9所示.

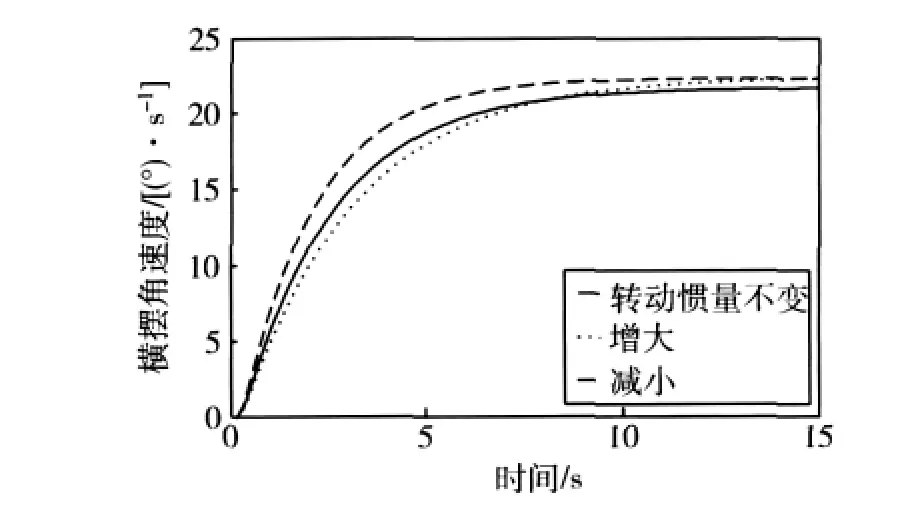
图9 出弯时横摆角速度响应对比

转动惯量改变后，赛车仍然为过度转向.

赛车转动惯量为1 600 kg·m2时，固有频率为ω0为1.9 rad/s，阻尼比ζ为2.36.赛车转动惯量为1 000 kg·m2，固有频率ω0为2.09 rad/s，阻尼比ζ为1.98.由图9可见，增大或减小转动惯量对转向特性的影响很小.但是，减小转动惯量可以较大程度提高出弯时的响应速度.

5 结论

1)赛车无轴荷转移时为接近中性转向.入弯时减速造成的轴荷转移使赛车趋于不足转向，出弯时加速造成的轴荷转移使赛车趋于过度转向.

2)为了减少入弯时的不足转向，使赛车能够更快的进入弯道应适当较小轴距，但同时会增大出弯时的转向过度.而转动惯量的减小对赛车的入弯性能影响并不明显，但可较大程度提高赛车出弯时的响应速度.

[1] 倪 俊，徐 彬.方程式赛车尾翼作用的仿真研究[C].2011年中国汽车工程学会年会论文集，SAEC2011C027.北京:机械工业出版社.

[2] 倪 俊，徐 彬.基于ADAMS的FSAE赛车建模与操纵稳定性仿真 [J].工程设计学报，2011，18(5):354-358.

[3] 倪 俊，徐 彬.FSAE赛车双横臂前悬架运动学仿真及优化 [J].车辆与动力技术，2011，4:51-54.

[4] 余志生.汽车理论 [M].北京:机械工业出版社，2000.

[5] 郭孔辉.汽车操纵动力学[M].吉林:吉林科学出版社，1993.