三体船操纵与横摇耦合运动试验与分析
马天宇,崔 健,杨松林
(江苏科技大学船舶与海洋工程学院,江苏 镇江 212003)
0 引言
高速船操纵性在船舶的所有水动力性能中,是研究的最不成熟的,因此也是最值得研究的问题之一。近年来,造船界对船舶操纵性研究十分重视,在船舶操纵运动数学模型、船舶操纵运动水动力、船舶操纵运动模拟仿真和船舶操纵控制方面都取得了显著的进展。国内外对三体船的研究已广泛展开,但在三体船的操纵性方面研究比较少。意大利CETENA船舶研究所改进了常规单体运输船操纵性仿真程序SIMUP,使其适用于三体船的操纵性预报,并计算分析得到不同侧体纵向位置对三体船航向稳定性和回转能力的影响[1]。卢晓平等采用一阶KT响应方程的数学模型对某三体船操纵性进行预报,计算得到三体船相关的操纵性参数,并与单体船的操纵性做了比较分析,为三体船操纵性精确预报、操纵性模型试验研究以及操纵性改进等后续研究创造了条件[2]。
横摇是船舶在波浪中最容易发生的运动形式,而且在各种摇荡运动中幅值最大[3]。三体船横摇运动的纯理论计算比较困难,因此目前预报三体船横摇运动较为可靠的方法仍是模型试验[4]。当三体船横摇时,侧体将发生升沉与横摇的耦合运动。但是侧体的升沉阻尼比横摇阻尼大得多,忽略侧体的横摇运动而将其简化为只做升沉运动,这种简化与高速三体船实际的横摇运动比较接近[5]。Francesccuto采用主、附体皆为wigley船型的模型对三体船的横摇运动进行了数值仿真和实验研究,该文基于以下2个理论模型假设:①横摇过程中主船体做类似单体船的横摇运动;②两侧体的运动简化为伴随主体做升沉运动。从物理概念上说,这种理论模型与高速三体船实际的横摇运动较为接近,其理论计算结果与模型试验结果的比较亦在一定程度上验证了该理论模型的有效性[6]。李培勇等通过三体船模型横摇试验中变化的侧体横向位置,并对侧体安装舭龙骨进行对比试验,研究侧体布置和舭龙骨对三体船横摇运动的影响[7]。
本文基于Visual Basic 6.0编写了一套遗传算法系统辨识程序。该程序可通过限定约束条件对水面三体船模操纵和横摇的试验数据进行辨识。最后对结果进行分析,验证该方法的可行性。
1 辨识方法
在本文对三体船模运动的辨识中,首先通过船舶操纵性与船舶横摇相关知识推导出船舶操纵性与船舶横摇相关的待辨识数学模型,并确定待辨识模型参数。在对模型待估参数的辨识过程中笔者利用VB平台编写了数学模型程序,选择遗传算法,通过选择、交叉、变异来寻求最优解。
1.1 三体船操纵运动回转数学模型
试验变量为回转速度和舵角,因此可以将回转直径表达成回转速度和舵角的表达式,即:D=F(V,δ),由试验数据可以看出,回转直径与速度成正相关,与舵角成反相关,故选取

式中:D为船模回转直径;V为回转速度;δ为舵角。
目标函数选取:
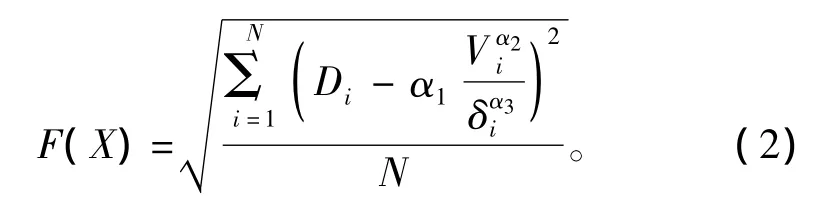
式中:α1,α2和 α3为待辨识参数;N为试验记录的次数。
1.2 三体船横摇运动数学模型
三体船自由横摇运动方程式为
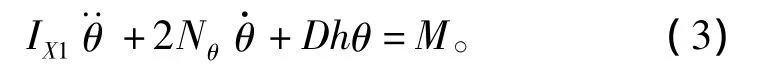
式中:D为排水量;IX1为总惯性矩由船体惯性矩和附加惯性矩2部分组成;Nθ为线性阻尼系数;h为初稳性高;θ,,分别为横摇角、横摇角速度及横摇角加速度,其中θ,为必要状态参量;M为外界力矩为控制参量。
将式(3)变形后,得到
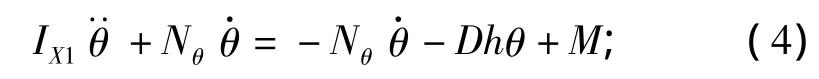
将式(4)写成矩阵形式:
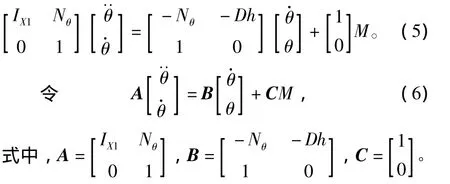
将式(6)等号左边进行离散,得
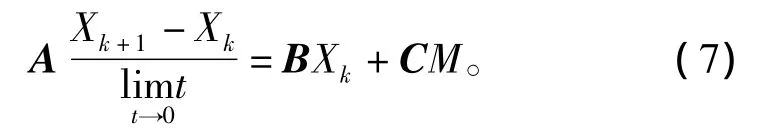
式中:Xk为横摇过程中第k时刻的输入参数的采样值;t为采样周期。
把式(7)中行矩阵变形,得
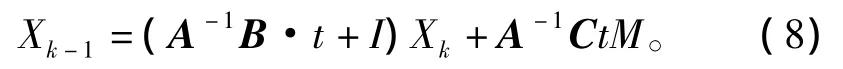
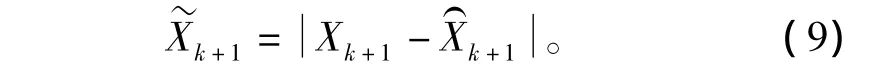
由线性代数的知识可解得
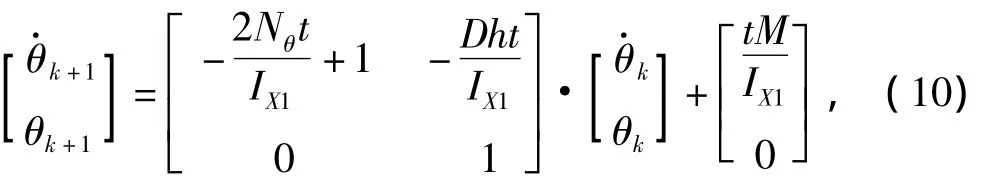
则有k+1时刻下的误差估计准则:
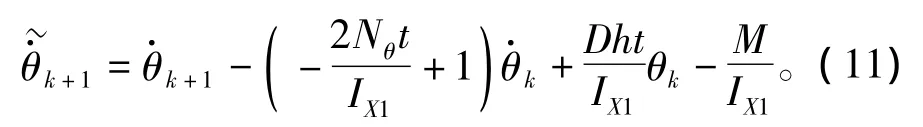
由此得到k+1时刻下最优状态估计基本公式(损失函数)为
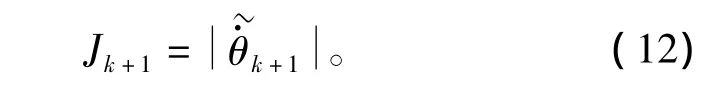
由于外力矩不易得到,故推导得到i时刻的误差估计准则:
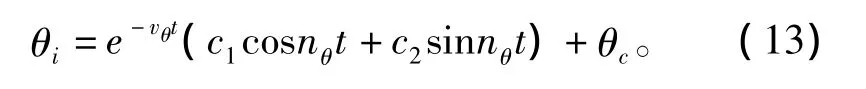
式中:θi为第i时刻的横摇角;nθ为船舶横摇固有圆频率。
得到新的优化函数为
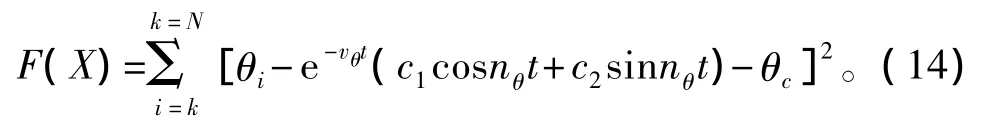
选定 vθ,c1,nθ,c2,θc为设计变量,并对其进行优化;N为采样数据的个数。
2 试验分析
2.1 试验方案
选用某三体船模在江苏科技大学游泳池进行回转试验。

图1 三体船模做回转运动Fig.1 The trimaran model rotation test

表1 回转试验条件Tab.1 Rotation test conditions
三体船模的侧体横距和侧体纵距如图2所示,其中b为附体横距,l为附体纵距。
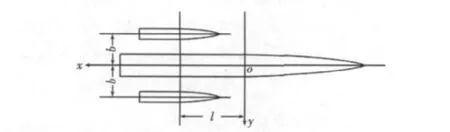
图2 三体船模侧体横纵距示意图Fig.2 The outriggers of trimaran model vertical and horizontal distance schematic diagram
试验数据分为2组记录,第1组的电压分别为1.8,2.0和2.2 V,舵角 (左舵)分别为30°,35°和40°。第2组为电压1.8 V时,侧体状态分别为竖直,向外侧倾20°,向内侧倾斜20°时的组合试验数据,如表2所示。
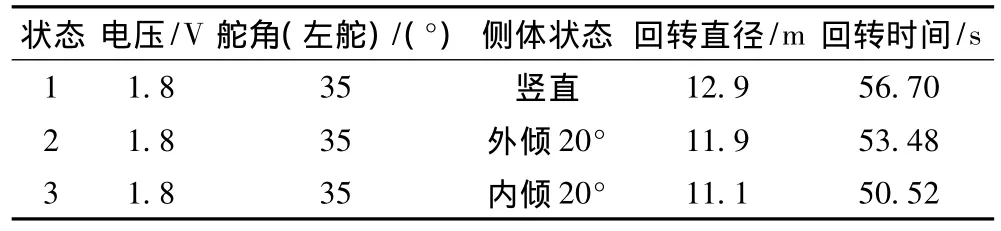
表2 回转试验数据Tab.2 Rotation test data
2.2 操纵运动辨识结果
图3为操纵运动辨识程序界面。

图3 操纵性系统辨识程序界面Fig.3 Maneuverability system identification program interface
选取回转试验中得到的15组数据进行辨识计算,其中设计变量上下限为a1∈[215,220],a2∈[0.03,0.05],a3∈[0.5,1],取交叉概率为0.8,变异概率为0.1,种群20个,遗传代数100代进行系统辨识。辨识结果为:a1=216.1729,a2=0.0349,a3=0.7174,得到回转直径方程为

系统辨识数据和试验数据列于表3。由表3可以看出,大部分辨识得到的直径与原始回转直径的相对误差保持在10%以内,只有状态5和状态6的相对误差偏大,原因可能因为试验时起风在水面产生了波浪,对三体船的回转运动造成一定影响。总体来讲,辨识结果与原始数据拟合度较好,辨识结果比较满意。
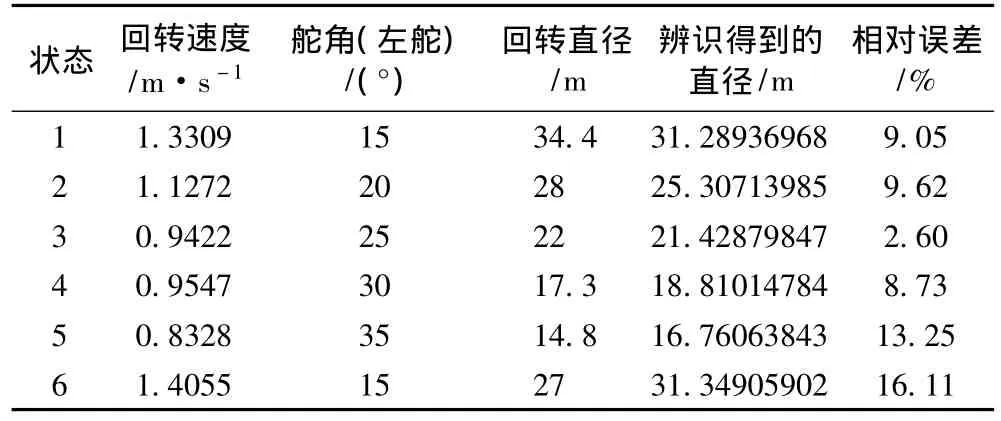
表3 辨识数据与试验数据对比Tab.3 The identification data and the experimental data comparison
2.3 横摇运动辨识结果
图4为横摇运动辨识程序界面。
考虑到三体船模在回转过程中的横摇角随时间变化的曲线“毛刺”较多,故表2所示3种状态下笔者仅选取了其中的6 s、4 s和3 s时间下的横摇角变化进行系统辨识,其中设计变量上下限为vθ∈[0.05,0.1],c1∈[-1,-0.1],nθ∈[4.5,5.5],c2∈[-1,-0.1],θc∈[-3,-2],取交叉概率为0.8,变异概率为0.1,种群30个,遗传代数200代。辨识数据与试验数据的对比如图5~图7所示。
当侧体为竖直状态时,辨识结果为:vθ=0.081,c1= -0.258,nθ=4.946,c2= -0.308,θc= -2.481,此时的横摇角方程为

当侧体为外倾20°状态时,辨识结果为:vθ=0.057,c1= - 0.344,nθ=5.416,c2= - 0.101,θc=-2.807,此时的横摇角方程为
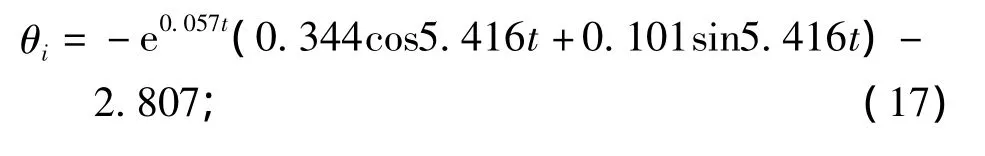
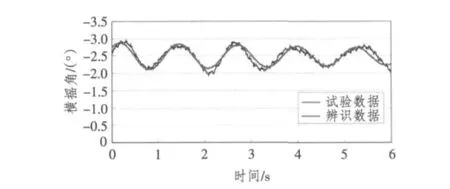
图5 侧体竖直状态下辨识数据与试验数据的对比Fig.5 The identification data and the experimental data comparison in the state of vertical outriggers
当侧体为外倾20°状态时,辨识结果为:vθ=0.053,c1= -0.161,nθ=5.236,c2= -0.427,θc= -2.218,此时的横摇角方程为
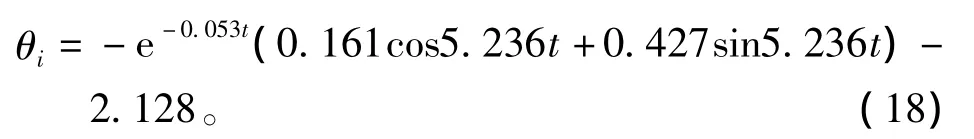
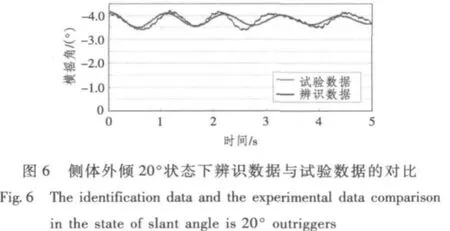
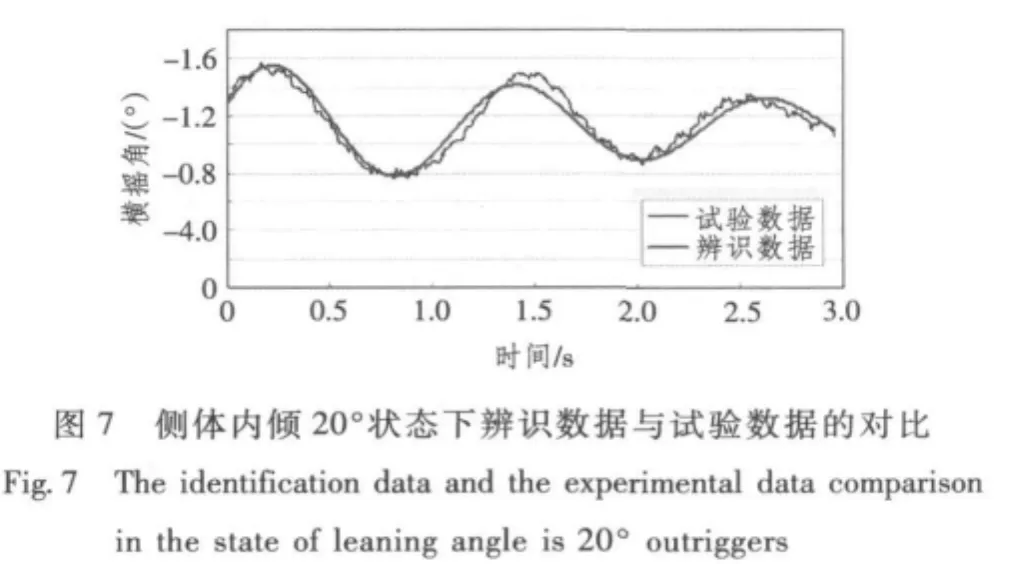
从3种侧体状态下辨识数据与试验数据的对比可看出,辨识得到的横摇角曲线与试验得到的横摇角曲线变化趋势保持一致,拟合度也比较好。对于个别区间出现的误差,如图5中2.8~3.2 s,5.4~6.0 s,图6中2.2~3.0 s,4.4~5.0 s和图7中 1.4~1.6 s,其原因可能有以下两方面:一方面是回转试验过程中风和水面波浪等其他环境因素的干扰,另一方面是所选横摇数学模型自身的局限。
3 结语
本文通过三体船模回转试验,获得了15组不同状态下回转直径的试验数据以及同一电压下不同侧体状态的三体船模横摇角变化数据,然后用基于VB语言改编的遗传算法程序分别对三体船模回转直径和横摇角进行了系统辨识,得到了较好的辨识结果,验证了该系统辨识程序的可行性。
[1]LUCA S,ROBERTA D,MICHELE V,et al.Design project of a tramaran multipurpose frigate:Study of the hydrodynamic aspects[C]//Proc.of the 7th International Conference on Fast Sea Transportation FAST 2003.Napies:FAST 2003,2003.
[2]卢晓平,姚迪,王波.三体船操纵性计算与特性分析[J].海军工程大学学报,2009,21(1):47 -53.LU Xiao-ping,YAO Di,WANG Bo.Trimaran maneuverability prediction and its feature analysis[J].Journal of Naval University of Engineering,2009,21(1):47 -53.
[3]李积德.船舶耐波性[M].哈尔滨:哈尔滨工程大学出版社,2007.
[4]刘宇辰,任毅,蔡新功,等.三体船横摇运动试验研究[J].船舶,2011,22(2):20 -23.LIU Yu-chen,REN Yi,CAI Xin-gong,et al.Experimental research on trimaran rolling[J].Ship & Boat,2011,22(2):20-23.
[5]赵连恩,谢永和.高性能船舶原理与设计[M].北京:国防工业出版社,2009.
[6]FRANCESCUTTO A.On the roll motion of a trimaran in beam waves[A].The 11th International Offshore and Polar Engineering Conference(ISOPE 2001)(V01.1.III)[C].Stavanger,2001.
[7]李培勇,冯铁城,裘泳铭.三体船横摇运动[J].中国造船,2003,44(1):24 -30.LI Pei-yong,FENG Tie-cheng,QIU Yong-ming.Investigation of trimaran roll motion characteristics[J].Shipbuilding of China,2003,44(1):24 -30.
[8]王勇,杨松林,范凯.五体船横摇运动模式分析方法研究[A].2008年船舶水动力学学术会议暨中国船舶学术界进入ITTC 30周年纪念会,杭州,2008.

