管路支架谐波响应特性分析及简化模型的建立
王永胜,张京伟,吴崇健,吴声敏
(中国舰船研究设计中心,湖北 武汉 430064)
0 引言
管路支架是船舶管路系统的一个重要组成部分。在1艘船舶中,管路支架的数量较大且种类较多。在对管路系统进行动力学分析时,如果对管路支架进行实体建模,会使计算成本过大。Lennart G.Jansson和LING Fu-zeng在文献 [3]中指出,在以往的工程经验中,对支架的建模和计算往往占据了整个管道系统分析预算的1/3。由此可以看出,建立合适的管路支架模型对于实际工程的重要意义。文中还总结了目前常用到的3种支架模型尝试:①把支架总体看成刚性约束;②把支架看成弹性约束;③在满足某种标准时看成刚性约束,而其他情况下就要考虑其弹性因素。其中把支架看成弹性约束时,往往是采用单自由度弹簧和阻尼来代替,而忽视了支架本身质量的影响。本文将首先对船舶中较常见的管路支架进行频域分析,然后在此基础上提出二自由度简化模型。
1 管路支架的频域特性分析
1.1 研究对象
由于管路支架的种类较多,这里选用1种船舶中较常见的管道之间为55 mm的马脚型管路支架作为研究对象。这种管路支架根据橡胶材料和卡箍的关系又可分为2类:一类是橡胶与卡箍相互独立;另一类即橡胶与卡箍黏接在一起或卡箍包裹在橡胶里面,参见图1。

图1 2种类型的马脚型管路支架结构Fig.1 Schematic diagram of two kinds of piping supports
图1中的2种管路支架有个共同点,即由多个构件组成,构件与构件之间存在着接触关系,整个结构通过螺栓预紧来实现紧固。
1.2 频域分析
利用Ansys软件中的谐响应分析模块对管路支架进行频域特性分析。这里选用图1中第2种管路支架作为计算对象,这种管路支架又叫硫化马脚,其卡箍由钢片和包裹在外面的硫化橡胶组成。Ansys提供了3种谐响应分析方法[2]:完全法、缩减法和模态叠加法。3种方法各有优劣,本文选用模态叠加法进行分析。这是因为研究对象是一个多构件结构,包含接触非线性 (在小变形情况下可忽略材料非线性),不同构件通过螺栓预应力紧固在一起。这一过程可通过预应力计算来实现,而模态叠加法支持预应力效果,然后在此基础上进行含预应力的谐响应分析。
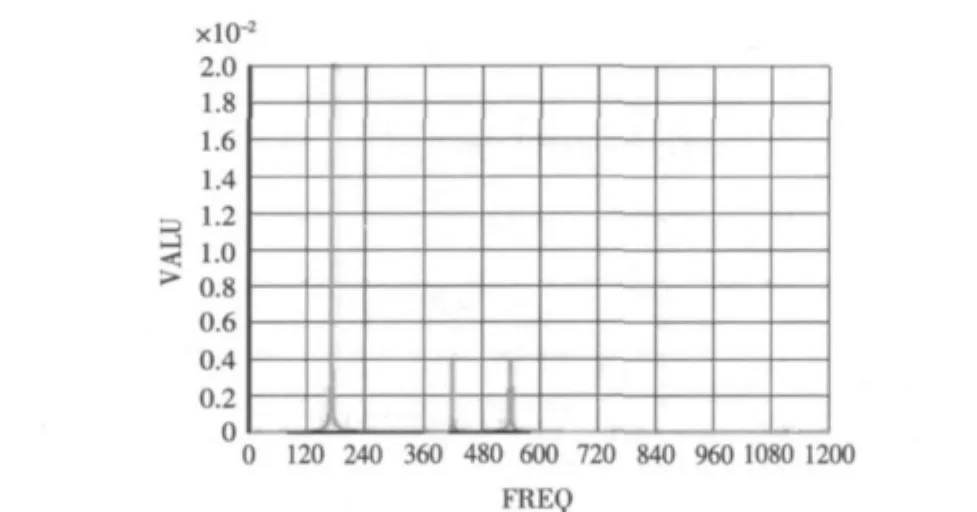
图2 无阻尼时管的垂向位移响应曲线Fig.2 Displacement response curve of pipe in the vertical direction without damping
先不考虑阻尼,为减小计算成本,管长取0.1 m,结构用体单元模拟,管道端面设置对称约束,在管道两端分别加载幅值为100 N,频率范围0~2000 Hz的垂向或横向载荷进行计算。加载垂向载荷时,计算得到频域内管的垂向位移响应曲线如图2所示。
由图2可知,在频率0~1200 Hz范围内,管道有三阶模态被激发,分别对应的频率为170.19,420.15,539.52 Hz,选取被激发的前二阶模态,列出其振型如图3所示。

图3 垂向被激发的前二阶模态振型Fig.3 The first two excited modal shapes in the vertical direction
管道除了受到垂向激励的作用外,还可能受横向激励的作用。在加载横向激励作用下管道的横向位移曲线如图4所示。
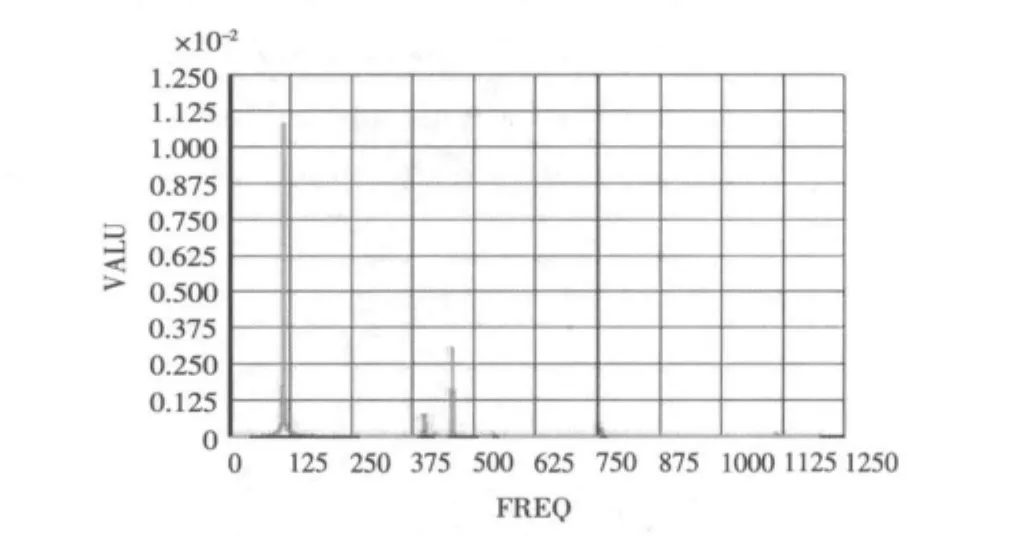
图4 无阻尼时管的横向位移响应曲线Fig.4 Displacement response curve of pipe in the horizontal direction without damping
图4中被激发的前三阶模态对应的频率分别为110.81,398.58,456.08 Hz,其中第一和第三阶被激发的响应比较明显,列出这二阶对应的振型如图5所示。
由上面的分析可知,管道的垂向和横向位移响应除由主振型被激发产生的主峰值外,还有由橡胶卡箍固有振型被激发产生的从属峰值,这也说明卡箍与支座的固有特性会对管道响应产生影响,在建立简化模型时必需要考虑到这点。

图5 横向被激发的二阶模态振型Fig.5 The first two excited modal shapes in the horizontal direction
实际上,由于管路支架包含橡胶材料,因此在分析中应该考虑阻尼的影响,通过设置一定的材料阻尼计算得到的管道垂向和横向位移响应如图6所示。
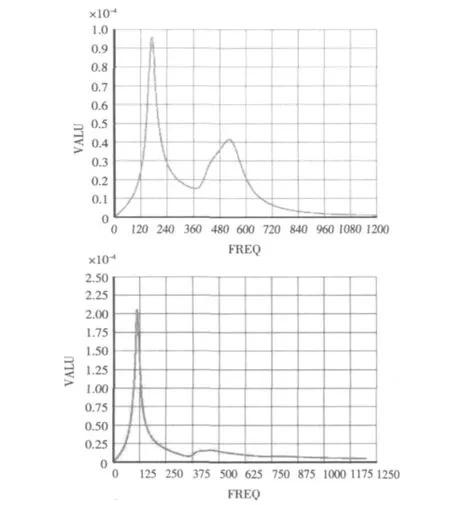
图6 含阻尼时管道的垂向和横向位移曲线Fig.6 Displacement response curves of pipe in both directions with damping
与前面无阻尼时管的位移响应曲线相比,由于阻尼对振动的衰减作用,有阻尼位移响应曲线的各个峰值明显降低。另外,与无阻尼响应曲线相比,图6中曲线的共振峰个数减少了,特别是无阻尼响应曲线中的第2和第3个共振峰在有阻尼的情况下合成了1个共振峰,这是因为二者对应频率相近,峰值还来不及衰减就进入了下1个共振峰。因此在对硫化马脚建立简化模型时不能简单地用单自由度模型代替,应至少包含2个自由度。
2 管路支架简化模型的建立
在以往对管路系统的分析中,一般都是用单自由度的弹簧—阻尼系统来模拟管路支架[4]。这样的处理方式在一定程度上可以满足工程分析的要求,但它忽视了支架本身固有特性的影响。由前面的分析可知,不考虑阻尼时,管道在垂向和横向2个方向上的响应在低频范围内存在多个共振峰。由于影响管道响应的主要是低阶模态,因此在建立简化模型时可以只取前面几个共振峰而忽略掉高阶共振峰的影响,这里取2个共振峰,如果第2和第3个峰值比较接近,则将二者合并,组成1个共振峰。这样含2个共振峰的响应曲线与二自由度系统的响应曲线相似,因此可以考虑在2个方向分别用二自由度质量-弹簧-阻尼系统来简化管路支架,具体模型如图7所示。

图7 二自由度简化模型图Fig.7 Two-degree-of-freedom modals
不考虑阻尼时,上面的二自由度系统包含M1,K1,M2,K2共4个参数。M1已知,为0.1 m长管的质量,这里等于0.386 kg;M2是中间质量块的质量,它并不是简单地等于管路支架的质量。因此,4个参数中有3个未知,欲得到这3个未知参数,则必须要有3个方程。二自由度系统具有二阶固有频率,若要用它来模拟实际的管路支架,则必须使这二阶固有频率等于前面无阻尼谐响应分析中被激发的前二阶模态对应的频率,据此可以得到2个方程。据振动理论,无阻尼二自由度系统的运动微分方程为
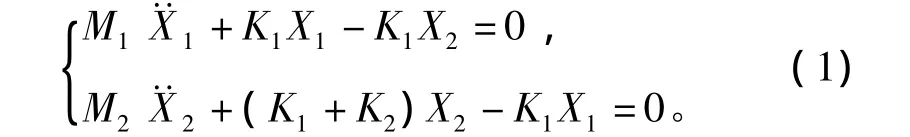
求解特征方程可得到系统的固有频率
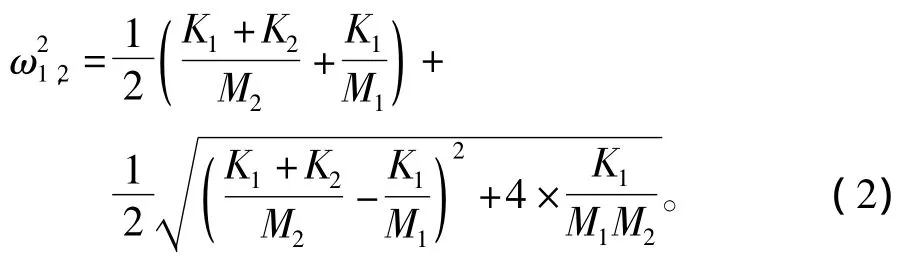
已知ω1和ω2,这样就得到了2个方程,另外还需1个方程就可以求得3个未知参数。第3个方程可以通过2种方式来建立,一种是通过模态振型来确定,对于上面的两自由度系统,当它按某一固有频率作简谐同步运动时,M1和M2运动的振幅之比是一个确定的量,由系统本身的物理性质所决定[1],这个比值为

式中:u1和u2分别为M1和M2的运动幅值,右上角括号内的数字代表阶数;r1,2分别为M1和M2在第一阶固有频率和第二阶固有频率时的振幅之比,这个比值可以从前面管路支架无阻尼谐响应分析的结果中得到。假设u1为管路第一阶的运动幅值,u2也取支架上某一点的第一阶的运动幅值,这样就构成了第3个方程。
另一种方法根据模态质量的性质来建立第3个方程。模态质量可以理解为结构实际参与某一阶模态运动的质量,因为在结构中各部分参与模态运动的程度是不一样的,所以模态质量一般不是已知的结构质量。在Ansys提供的模态分析中能够通过归一化处理提取任一阶模态质量,因此也可以提取本文关心的某一个被激发的振型对应频率的模态质量 M'(r),然后代入式(4)得到第3个方程。
对于一个多自由度度系统,其模态质量M(r)可由下式得到:

式中:{u(r)}为模态矢量矩阵;[M]为系统质量矩阵,将它进行归一化处理可得到M'(r)。对于本文关心的二自由度系统,可取第一阶模态质量,它对应于实体模型中第1个被激发的固有模态对应的模态质量M'(1),可得到以下方程:

式中,r为二自由度系统第一阶模态振型的幅值之比,可由式(3)得到。M'(1)由软件计算给出,这样就确立了第3个方程,由这3个方程就可以求得3个未知参数了。下面根据前面的分析分别确定2种管路支架简化模型的各个参数。
在确定硫化马脚型支架简化模型的参数时,这里采用第2个方法即提取模态质量来建立第3个方程。考虑到图2中管道垂向被激发的三阶频率中第二、三阶频率比较接近并且与第一阶相距较远,故可将二者合并成1个频率,取中间某个值,这样得到简化模型的前二阶频率为170.19,456 Hz,频率为170.19时从Ansys计算中提取的模态质量为0.4684 kg,这样代入3个方程解得垂向模型的K1,M2,K2分别为9.21e5,0.3037,1.2e6(国际单位制);另外,由图4位移响应的特点,取第一和第三阶被激发的频率110.81,456.08 Hz作为简化模型的二阶频率,第一阶频率对应的模态质量为0.525 kg,将它们代入3个方程解得横向模型的K1,M2,K2分别为9.7451e5,0.2114,3.2842e5。
以上建立了该类型支架的简化模型。
3 简化模型的验证
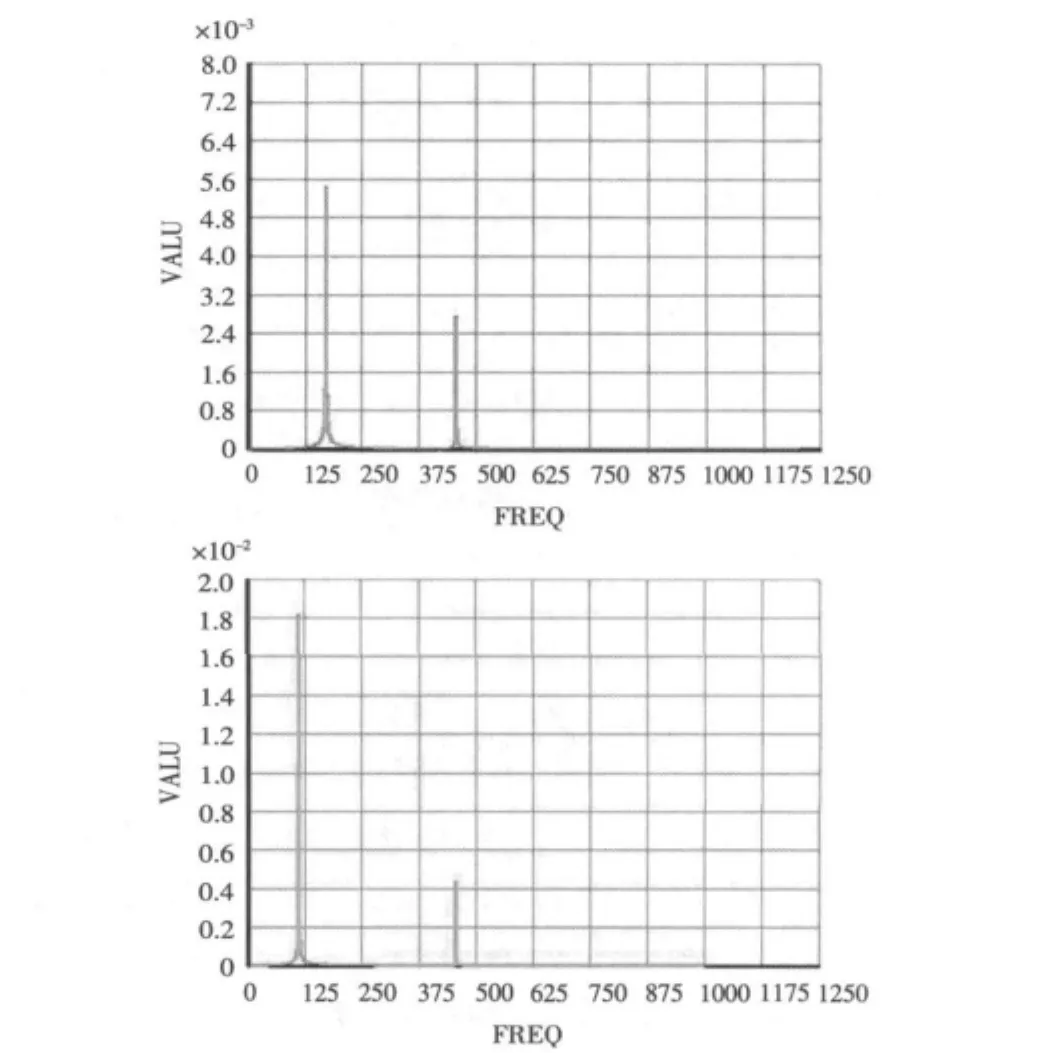
图8 支架简化模型管的垂向和横向位移曲线Fig.8 Displacement response curves of pipe in both directions of simplified model
为验证简化模型的可靠性,利用Ansys软件对该简化模型分别进行检验计算。其中管道用梁单元beam188,截面尺寸和长度与前面的实体模型相同,管路支架用2组弹簧阻尼单元combin14和质点单元模拟,施加相同的激励和约束条件。不考虑阻尼时,计算得到支架简化模型中管道的垂向和横向位移曲线,如图8所示。

将图8与图6对比,支架简化模型中管道在2个方向的位移响应被激发的频率与实体模型相近,只是响应的幅值有差别,但这可以通过调整阻尼来消除。假设支架固定在一块厚2 cm,边长为2 m的简支钢板上,通过设置合适的单元阻尼和材料阻尼,进一步求得支架简化模型中管道响应曲线如图9所示。
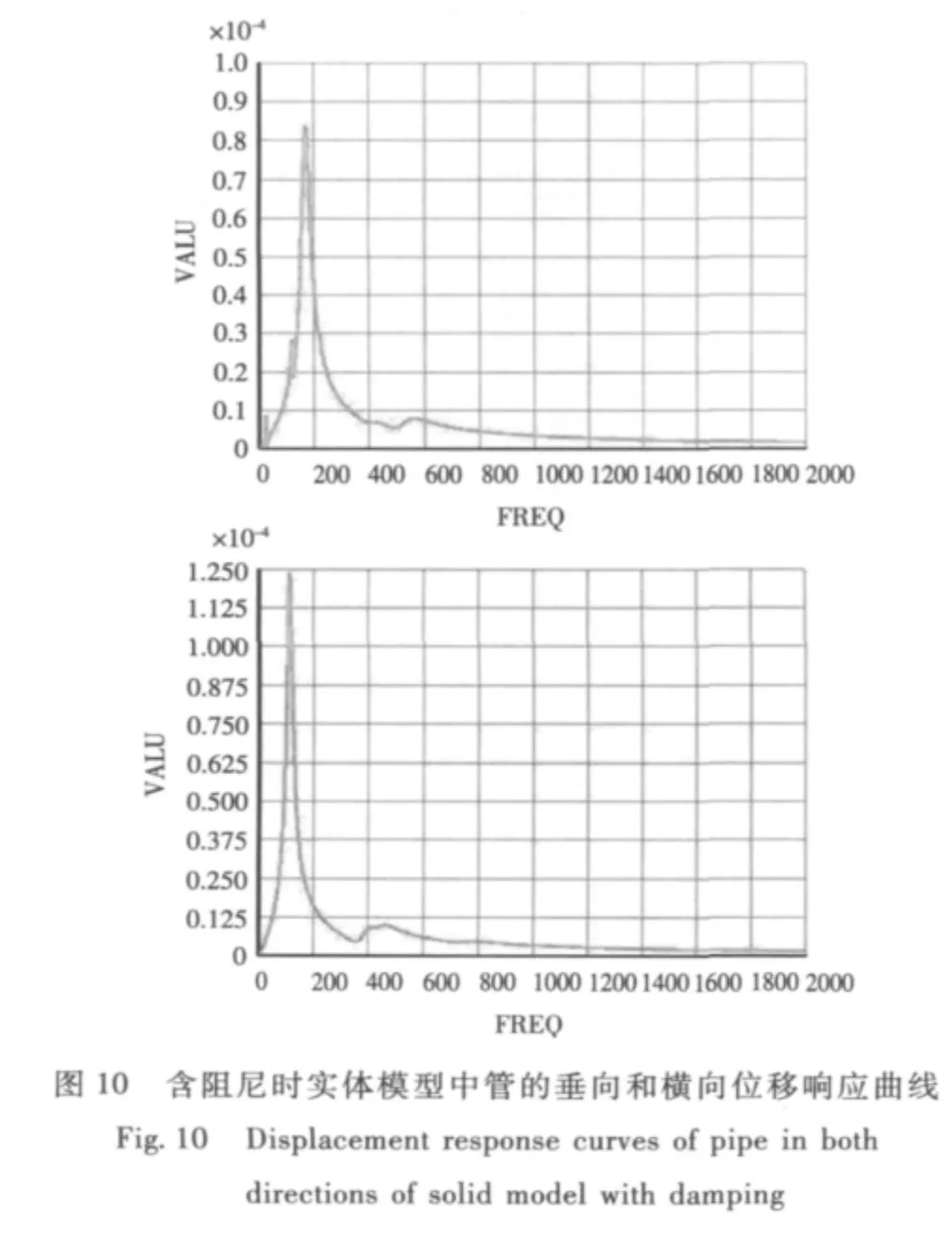
在相同条件下得到管路支架实体模型中管道的响应曲线如图10所示。
图9与图10相比,2种情况下曲线共振峰的位置和峰值大小几乎是一样的。因此,从这一点可以看出,简化模型在设置合适阻尼的情况下是能比较准确地模拟管道位移响应的。
4 结语
本文通过对管路支架实体模型进行含预应力的谐响应分析,了解支架的频域特性,并在此基础上建立了垂向和横向2个方向的二自由度简化模型。这种简化模型不同于以往单自由度模型,它充分考虑了管路支架本身质量对其动力学特性的影响。经过验算,这种简化模型在设置合适的阻尼情况下能很好地模拟管路支架在频域内的力学行为。另外要指出的是,这种模型没有考虑管路支架在多个方向存在耦合的特性,这虽然会对分析的结果带来一定的改变,但对整体结论的影响很小。因此,用这样的简化模型模拟管路支架在管路系统中动力学行为是合适的,这将在保证精度的基础上大大简化对管路系统的振动研究。
[1]师汉民,谌刚,吴雅.机械振动系统―分析……测试·建模·对策[M].武汉:华中理工大学出版社,1992.
[2]陈精一,蔡国忠.电脑辅助工程分析ANSYS使用指南[M].中国铁道出版社,2001.
[3]JANSSON G,ZENG Ling-fu.On modeling piping supports in dynamic analysis of nuclear-power piping system[C].Proceedingsofthe 16th InternationalConference on Nuclear Engineering,2008.
[4]蒋学武,朱石坚.船舶管道橡胶减振器的应用[J].海军工程大学学报,2000,(4):90 -91.JIANG Xue-wu,ZHU Shi-jian.The application of pipe rubber vibration isolators on warships[J].Journal of Naval University of Engineering,2000,(4):90 -91.

