基于二阶锥规划的平面阵近场等旁瓣波束优化

王华奎，王二庆

(1.水声对抗技术重点实验室，广东 湛江 524022;2.91388部队，广东 湛江 524022)

0 引言

矩形平面阵的远场和近场波束图均可以表示成2条相互垂直的线列阵波束图乘积的形式［1］。因此对平面阵的进行加权可以简化为计算2条相互垂直的线列阵的加权值，再用向量直积的方式来计算平面阵的加权向量。对于近场目标而言，由于目标距离阵列的距离不再是等差数列，因此在计算这2条相互垂直的线列阵的加权值时，常规的ChebyShev等方法将不再适用。本文提出使用二阶锥规划(Second order cone programming，SOCP)方法来计算这2条线列阵的近场加权值［2］，再通过向量直积来计算矩形平面阵的加权值，成功得到了平面阵在近场下的等旁瓣波束图。

1 平面阵波束图

如图1所示，该平面阵为矩形阵，阵元个数为N×M=NM，其中沿x轴和y轴的阵元个数分别为N和M，阵元间距均为λ/2，其中λ为窄带信号中心频率对应的波长。

设平面阵的近场扫描点到坐标原点的距离为Rp，其俯仰角和方位角分别为θp和φp。则第p个扫描点的坐标为

图1 三维坐标系和平面阵Fig.1 Three-dimensional coordinate system and planar array

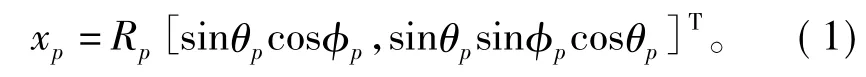
第(n，m)个阵元的坐标为

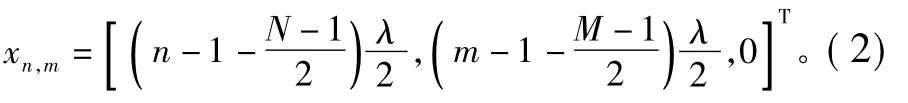
其中，n=1，2，…，N;m=1，2，…，M。

该扫描点到第(n，m)个阵元的时延可表示为2个坐标之差所得向量的二范数:

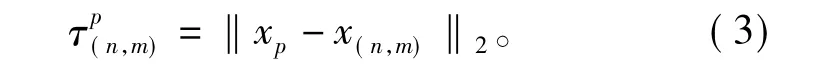
根据式(3)，平面阵的阵列流形可写为

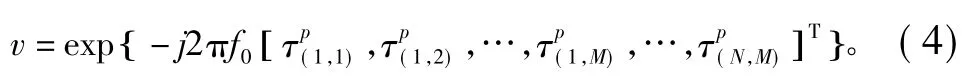
若平面阵的近场聚焦点到坐标原点的距离为R0，对应的角度分别为θ0和φ0，则该聚焦点到第(n，m)个阵元的时延可表示为

其中 x0=R0［sinθ0cosφ0，sinθ0sinφ0，cosθ0］T为聚焦点坐标。由式(5)可知，对应的加权向量为

式中:e表示向量点积;

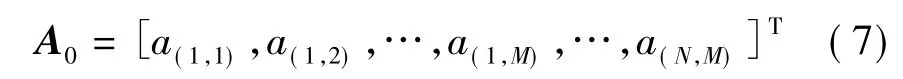
为幅度加权;

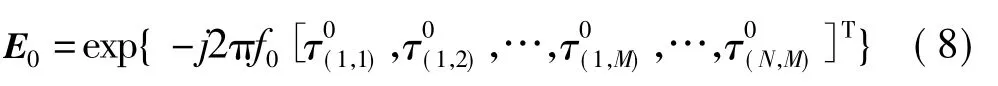
为相位加权。

平面阵的近场波束图可表示为

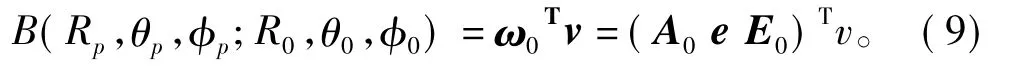
近场情况下，由于矩形阵的波束图可以表示为2个相互垂直的线列阵的波束图乘积，即式(9)可以重新写为

其中:Bx(Rp，θp，φp;R0，θ0，φ0)和 By(Rp，θp，φp;R0，θ0，φ0)分别为沿x轴和y轴的均匀线列阵的近场波束图，其表达式分别为

式中⊗为向量直积。

根据式(10)～式(15)，对1个矩形平面阵的波束形成可以分解为对2个线列阵进行波束形成。先计算出2个线列阵的加权向量，再通过向量直积就可以得到该平面阵的加权向量。

2 二阶锥规划下的平面阵近场波束图

由于阵列工作在近场，因此一般用于远场的等旁瓣加权方法如Chebyshev加权方法将不再适用。为了获得等旁瓣的波束图，本文使用二阶锥规划方法(Second order cone programming)。

SeDuMi［2］是由Sturm开发，用来处理对称锥优化问题的MATLAB工具箱。该工具箱可以用来求解二阶锥和线性约束下的凸优化问题。将其用于处理波束优化问题，可以达到寻优方法规范、精确性高的目的，并且具有计算量小和计算精确等优点。对于优化问题无解的情况也能自动判别，以便修正参数继续计算。

文中的等旁瓣问题可以转化为SeDuMi中的最低旁瓣约束问题。该问题可以描述为:保证主瓣波束与期望波束的误差小于某值，计算出一组加权值，使得波束旁瓣最低［3］。

式中，B(θs)为旁瓣区域的波束;Bd(θm)和 B(θm)分别为期望主瓣和设计主瓣的波束;ΘML为主瓣区域。

3 波束图仿真

仿真中，矩形阵位于xoy平面，几何中心坐标为(0，0，0)m，其沿x轴和y轴的间距均为1 kHz声波对应的波长的一半。阵元个数为12×12=144，其中N=12，M=12。近场聚焦点的俯仰角和方位角分别为(θp，φp)=(0°，0°)，该点坐标为(0，0，10)m。矩形阵及聚焦点的关系如图2所示，近场中使用Chebyshev和SOCP法获得的波束图如图3所示 (旁瓣级控制为-30 dB)。

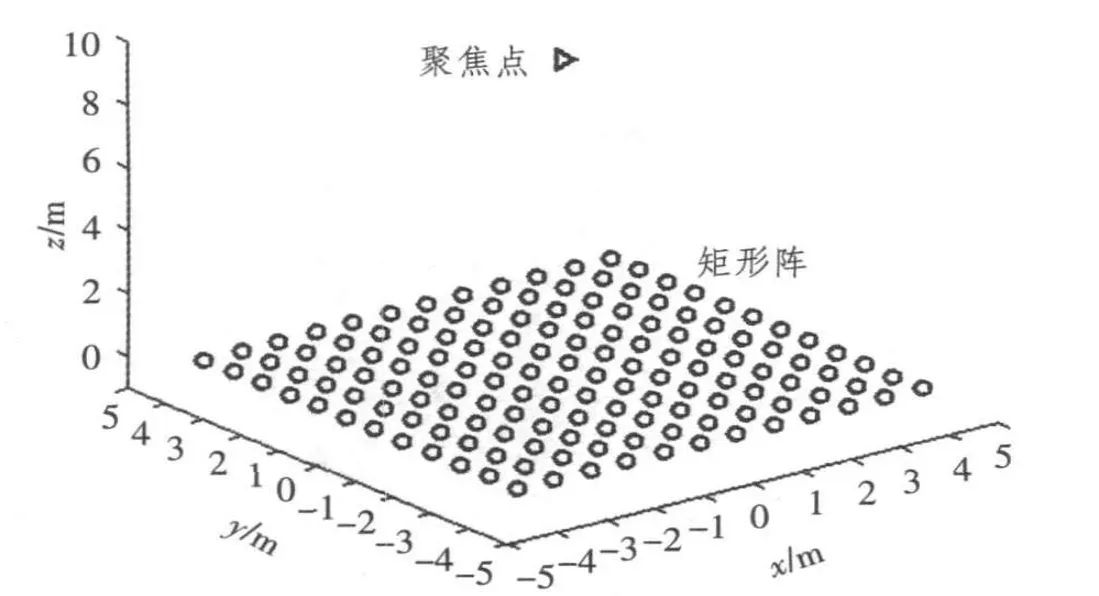
图2 矩形平面阵以及聚焦点示意图Fig.2 Sketch map of rectangular planar array and focal point

由图3(c)和图3(d)可知，在近场下，常规的Chebyshev方法获得的波束图第一旁瓣较高，并没有获得等旁瓣的效果。而SOCP方法可以获得近场下的等旁瓣波束图。图3中，ux=sin(θp)cos(φp)，uy=sin(θp)sin(θφp)。

为了考虑更实际的情况，设定矩形阵的阵元位置具有随机误差。该随机值服从均值为0，方差为1/15的高斯分布。分别利用Chebyshev加权和SOCP法来进行波束优化，所得结果如图4所示。

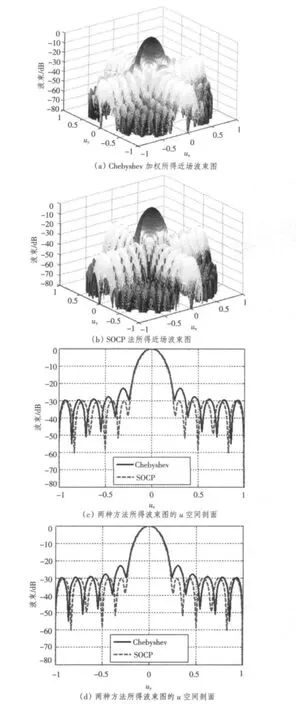
图3 近场下，分别使用Chebyshev和SOCP两种方法所得波束图Fig.3 Beam scheme in near field with Chebyshev and SOCP method respectively

图4 阵元位置存在随机误差时，分别使用Chebyshev和SOCP两种方法所得矩形平面阵的近场波束图Fig.4 Beam scheme in near field for rectangular planar array with Chebyshev and SOCP method respectively when there are random errors of array element position

由图4可知，当阵元位置存在误差时，利用Chebyshev获得的波束图的旁瓣太高，有的甚至超过了－20 dB。利用SOCP法获得的波束图，其旁瓣有轻微的抬高 (约为－28 dB)，但是波束图仍保持等旁瓣特性，其结果是可以接受的。

4 结语

本文研究了近场情况下矩形平面阵的波束优化。将矩形阵的波束图等效为2个相互垂直的线列阵的波束图乘积，通过计算这2个线列阵的加权并通过向量直积的形式来获得矩形阵的加权值。仿真结果表明，近场情况下，常规的Chebyshev方法已无法获得等旁瓣波束图，而SOCP法可以获得等旁瓣波束图。当阵元位置存在误差时，常规Chebyshev法的波束图发生严重畸变，而SOCP法获得的波束图，除了旁瓣级略微抬升2 dB外，其仍然是等旁瓣波束图。这些说明近场情况下，SOCP法比Chebyshev法更稳健。

［1］VAN TREES H L.Optimum array processing:part 4 of detection，estimation，and modulation theory［M］.Hoboken:John Wiley＆ Sons Inc.，2002.

［2］STURM J F.Using SeDuMi l.02，a MATLAB toolbox for optimization over symmetric cones［J］.Optim.Meth.Softw.，1999，11(12):625 －653

［3］鄢社锋，马远良.基于二阶锥规划的任意传感器阵列时域恒定束宽波束形成［J］.声学学报，2005;30(4):309－316.