基于神经网络的GPS水准方法的研究与分析★
王宇亮 汪金花 张志敏
(河北联合大学,河北 唐山 063009)
0 引言
GPS测量经平差后的高程是以WGS-84椭球为基准的大地高HGPS,工程上经常使用的是以似大地水准面上为基准的正常高H0,两者之差通常称为高程异常。高程异常求解的精度取决于数学模型的准确性。求取高程异常拟合的方法多,常用的有多项式拟合法、Shepard曲面拟合法、多面函数法、样条函数法等。人工神经网络因其强大的自学习、自组织和自适应能力在非线性系统的预测中得到了广泛的应用。基于BP人工神经网络的GPS高程转换方法是一种自适应的映射方法,该方法没作假设,能够减少模型误差,但是存在着收敛速度慢、训练时间长、神经元个数难确定等问题。径向基函数(RBF)神经网络结构简单,有较强的非线性映射能力,适合于多变量函数的逼近,非常适合于空间散乱数据的拟合。本文分别将BP网络和RBF神经网络应用于GPS水准高程拟合研究,在此基础上,选择某一地区的GPS水准实测数据进行了高程拟合实验,并将得到的最后精度进行了比较分析。
1 神经网络进行高程拟合的原理
人工神经网络的输入与输出关系是一种高度非线性映射关系,如果输入结点数为n,输出结点数为m,则网络是从n维空间到m维空间的映射。由于GPS高程拟合的实质是求一个从二维平面坐标或者大地坐标到GPS点的高程异常的映射。对于样本集合X和输出Y,可认为存在某一映射G使:

即高程拟合是求出映射G,使得在某种意义下,G是函数模型的最佳逼近。
1.1 BP网络的基本原理
经典的BP神经网络结构是三层结构:输入层、隐含层和输出层。因此比较理想的BP神经网络结构应该是A×M×B的结构,又因GPS高程拟合的数学模型可以表达为:

即高程异常ζ和点位坐标(X,Y)有关,若输入层取2(即坐标X,Y),输出层取1(即高程异常ζ),则模型2×M×1为最佳选择。
1.2 RBF网络的基本原理
径向基函数网络(Radial Basis Function,简称RBF)是一种两层前向型神经网络,包含一个具有径向基函数神经元的隐含层和一个具有线性神经元的输出层。
输入信号传递到隐含层,隐含层有S1个神经元,节点函数为高斯函数;输出层有S2个神经元,节点函数通常是简单的线性函数。隐含层节点(基函数中心)以径向基函数为核函数,其对输入矢量产生局部响应,输出节点对隐含层节点的输出进行线性加权,从而实现输入空间到输出空间的映射,使整个网络达到函数逼近的目的。在构建网络的过程中,通过反复调整散布常数的数值来确定最好的拟合效果,最终完成高程内插的运算。
2 实例分析与研究
本文针对大范围内GPS高程拟合,选取试验数据为某市D级GPS网(平坦地区,区域面积约为300 km2)中40个GPS点进行了三等GPS水准联测,其部分数据情况如表1所示。

表1 已知数据情况(部分)
2.1 BP网络的应用实例
在三层网络的拟合中,适当地选择网络结构就可以实现任意精度逼近连续函数,使用BP网络解决实际问题,其网络结构的优化决定了网络特性的提高,成为拟合成功与否的关键。对于三层BP网络,输入层和输出层神经元数量都是由实际问题本身决定的。
BP网络的创建代码如下所示:
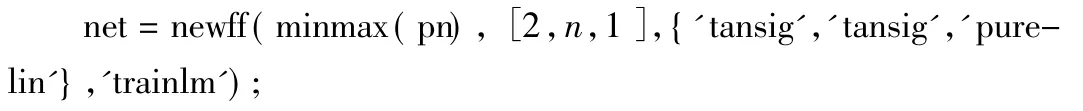
%创建BP神经网络,
%2表示输入层有两个输入,n表示隐含层神经元个数,1表示输出层数目,
%tansig,purelin为传递函数,trainlm为学习函数。

图1 GPS水准点联测平面示意图
确定网络结构,实际上就是确定隐含层神经元数目的多少,不同的网络结构在获得最佳的拟合效果时的隐含层神经元数目也是不同的。随着逼近函数的波动性增加,隐含层单元数应适当增加;随着学习样本数目增加,隐含层单元数目也应该适当调整。经过多次反复实验,最终确定学习样本为35,测试样本为5时的测试误差可以达到最小。图1表示了这40个均匀分布的已知点点位分布情况。
在网络的学习训练过程中可以看出,当隐含层神经元数目为6时的网络拟合精度最高,训练样本的最大误差最小,只有0.84 cm。因此,选用训练样本为35,测试样本为5,隐含层神经元数为6来构建网络结构,其训练后得到的测试样本的误差和其平均的中误差结果如表2所示。

表2 测试样本为5时的误差情况(一) mm
2.2 RBF网络的应用实例
用径向基函数网络实现函数逼近时,newrb()函数可以自动调整网络隐含层神经元数目,直到均方差满足精度或者神经元数目达到最大为止。其调用格式如下:
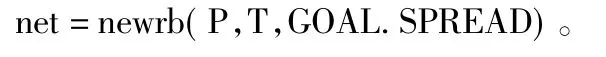
其中,P为输入向量;T为目标输出向量。
SPREAD为径向基层的散布常数,缺省值为1。
GOAL为训练精度。
在网络的设计中散布常数是一个非常重要的参数,下面我们就来看一下散布常数的选择对网络精度的影响。在下面的试验中我们已知数据中的35个已知点作为学习样本,其余的5个样本作为测试集,通过调整散布常数的不同数值来确定网络的最佳结构,在学习样本为35,测试样本为5,散布常数SPREAD=1.5时测试集的训练误差如表3所示。

表3 测试样本为5时的误差情况(二) mm
由以上实验可以看出,散布常数的确定对网络的拟合精度有很大的影响。散布函数需要足够大时才能覆盖所有的输入区间,但是如果其数值太大,则每个神经元的响应区域又会交叉过多,反而会使得精度有所降低。
因而,在此次的径向基函数网络设计中将散布常数SPREAD的值选为1.5,使得训练样本的最大误差值为0.84 cm,同时也保证了此时的拟合精度最高。
3 两种结构精度对比
1)随着学习样本的增加、测试样本的减少,测试样本的最大误差变得越来越小,因而,在设计网络的时候应该尽可能的选择较多的训练样本,从而保证利用训练后的神经网络得到的待定点的高程精度是最好的。
2)随着隐含层神经元数目的增加,网络的收敛次数逐渐增加,但是测试数据的最大误差在改变。通过实验发现,当隐含层神经元的数目为6的时候,网络的仿真误差最小,也就是说此时网络的拟合效果是最好的。
3)当隐含层神经元的数目增大到13及其以上时,测试集中的最大误差都超过了10 cm,但是,只是有一两个测试点的误差比较大。尽管如此,为了保证最好的拟合效果,隐含层神经元的数目也不能过多地通过以上BP网络和径向基函数网络的应用实例,得到BP网络和径向基函数网络的学习、训练误差情况如表4所示。

表4 BP网络与RBF网络的精度比较 mm
由表4可以看出,虽然径向基函数网络的最小学习误差明显小于BP网络的最小学习误差,并且除了径向基函数网络测试样本的最大误差值和BP网络的训练后的最大误差值相同,都为8.4 mm之外。BP网络的其他精度误差都比径向基函数网络的误差要小很多,尤其是BP网络训练后的平均中误差4.8 mm要比径向基函数的平均中误差5.7 mm小一些,因而BP网络训练后所得的拟合精度也相对比较高。
4 结语
本文以探究神经网络方法实现GPS高程异常拟合为目标,并结合具体的工程数据进行了神经网络性能分析,通过性能比较得出了基于BP神经网络模型在GPS高程异常拟合中具有较高的精度。
最后利用实验得到拟合后的网络结构完成测区内GPS水准的设计,实现待定点大地高到正常高的转换。但由于采集的数据量有限,故只能根据现有的数据和成果进行分析,对此提出以下建议:在地势平缓、经纬度相差较小的局部地区,在保证观测质量的情况下,联测数量越多的高等级水准点,采用GPS水准法可以获得越高的拟合精度;高程拟合起算点应尽可能的联测到高精度的已知水准点,已知高等级水准点在GPS网中的位置很重要,距离工程区越近,则通过已知点拟合的似大地水准面越接近工程区似大地水准面的现状,从而提高各个待定点的拟合高程精度。
[1] 黄张裕,冯 伟,陈苏娟.一种改进的GPS测定正常高方法的探讨[J].测绘通报,2007(8):36-39.
[2] 韩 硕.神经网络在GPS高程拟合中的应用[J].测绘通报,2006,8(4):48-50.
[3] 王殊伟,李 斐,柯宝贵,等.基于BP神经网络算法的GPS水准高程转换[J].武汉大学学报·信息科学版,2009,34(10):1190-1193.
[4] 杨明清,靳 番,朱达成,等.用神经网络方法转换·用神经网络方法转换 GPS高程[J].测绘学报,1999,28(4):301-307.
[5] 蔡昌盛,高井祥.面向MATLAB转换GPS高程的神经网络方法[J].四川测绘,2007,30(2):67-70.
[6] 胡伍生,华锡生,张志伟.平坦地区转换GPS高程的混合转换方法[J].测绘学报,2002,31(2):128-133.
[7] Nahavandchi H.The Direct Topographical Correction in Gravimetric Geoid Determination by the Stokes-Helmert method[J].Journal of Geodesy,2000(74):488-496.
[8] Kavzodu T.,Saka M.H.Modeling 1ocal GPS/leveling geoid undulations using artificial neural networks[J].Journal of Geodesy,2005,78(9):520-527.

