“热浴”环境下的非平衡输运过程

陈 娇

(黄冈师范学院物理与电子信息学院，湖北黄州438000)

1 微观模型

我们考虑一个具有N个自由度的有限系统，用自洽集体坐标方法(SCC)［1］，可以引入动力学系综坐标系(DCC)，将整个系统划分为两个子系统:集体系统和内禀系统，相应的自由度叫做集体自由度和内禀自由度。通常我们所关心的子系统是相关子系统。这样，整个系统在动力学上被分成两个子系统。

2 输运方程的微观推导

假设集体系统由单个粒子构成，其坐标、动量和质量分别为Q、P、M，为方便起见，令M=1。假设内禀系统是一个处于平衡态的“热浴”，即内禀系统满足正则平衡分布，而且满足各态历经条件。具体来讲，认为内禀系统由n(n→∞)谐振子构成，质量、坐标、动量和频率分别用mi、qi、pi和ωi表示。如果用(q，p)表示这 n 个谐振子的坐标和动量，则(q，p)是一组满足正则分布 ρ(q，p)=e－βHB(q，p)/Z 的变量，其中β=1/kT，Z=Trρ(q，p)，k是玻尔兹曼常量，T是热浴的温度，HB(q，p)是热浴的哈密顿量。为简单起见，只考虑一维情况。整个体系的哈密顿量可表示为:

H=HS+HB+HI

其中HS是集体系统的哈密顿量，HI是集体系统和热浴的耦合作用项，令

其中耗散记忆核:

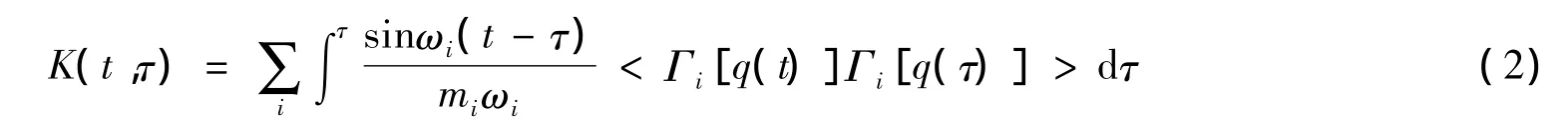
(1)就是广义Langevin方程。

如果内禀系统偏离平衡态不远，则可认为F(t)是一系列服从相同概率分布ρ=的高斯型变量的和，因此F(t)也是高斯型的。如果其平均值不等于零，则代表施加给系统一个平均力，可以对系统的哈密顿量进行修正，来将这个平均力作用包含进去，于是F(t)去掉这个平均值以后就是关于零点对称的变量了。也可以对耦合形式进行修正来去掉这个平均值［2］。

从(1)和(2)可以看出，耦合相互作用中热浴的具体形式并不会直接影响广义Langevin方程的一般形式，只会对耗散记忆核产生影响，也就是说耦合中热浴的作用是通过耗散记忆核对系统产生影响的。而耦合中集体坐标的具体形式则直接影响到广义Langevin方程形式。利用以上广义Langevin方程，我们可以讨论双线性和非线性耦合情况下的耗散机制。

假设耦合作用和系统坐标及热浴坐标都成线性关系，即

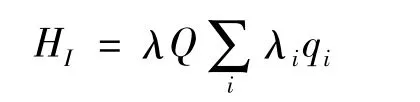
λi是集体坐标与第i个谐振子之间耦合系数，此时f(Q)=Q，Γi=λi，

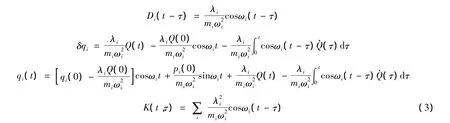
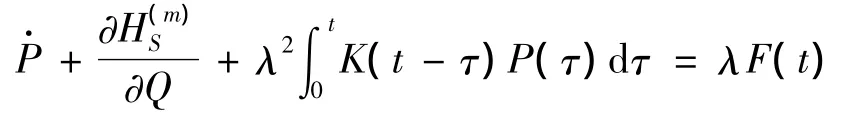
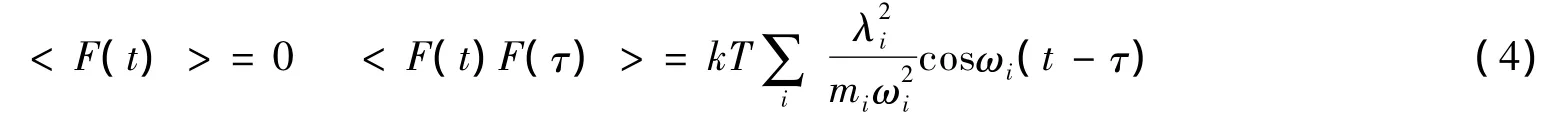
(3)和(4)比较可得涨落耗散关系:

＜ F(t)F(τ)＞ =kTK(t，τ)

从以上推导可以看出，如果耦合对集体变量是线性的，则此时集体系统的输运方程是有着加性噪声的线性Langevin方程。

如果耦合对集体和热浴坐标都是非线性的，例如

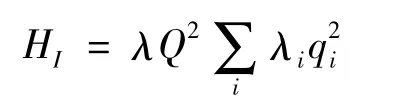
此时Γi=2λiqi，＜F(t)＞=＜λiq02(t)＞=，可令H'I= λQ2(Γ(q0)－ ＜ Γ(q0)＞)，

这种修正实际上只是在整体上使耦合作用发生了平移，并没有改变整个系统的性质。

令ξ(t)=F(t)－＜F(t)＞则有

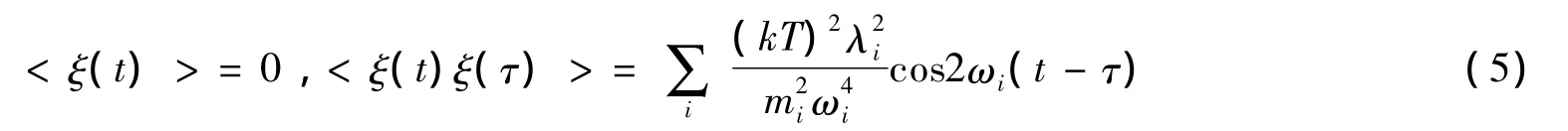
非线性耦合时集体系统的朗之万方程为:

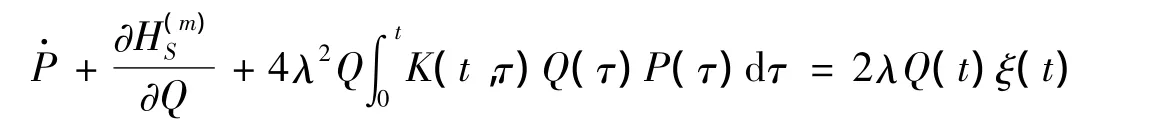
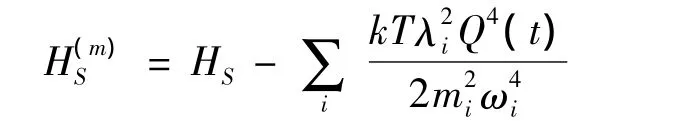
同样也满足涨落耗散关系:

＜ ξ(t)ξ(τ)＞ =kTK(t，τ)

可见如果耦合对集体变量是非线性的，则此时集体系统的输运方程是有着乘性噪声的非线性Langevin方程。

3 关联函数和响应函数

一般地，动力学响应函数 x(t，t－ τ)和关联函数 φ(t，t－ τ)［7］，与时刻 t以及时间间隔 τ都有关系，反应的是时刻t集体系统和内禀系统的瞬时性质，描述的是时刻t系统对外界涨落量的响应和不同时刻涨落之间的关联情况。但是当内禀系统到达与时间无关的稳定状态后，x(t，t－τ)和φ(t，t－τ)就与时刻t的选取无关了，只是时间间隔τ的函数。定义:

响应函数: x(t，t－ τ)=x(τ)=TrB{GHB(τ)B，B}ρHB

关联函数: φ(t，t－ τ)= φ(τ)=TrB{GHB(τ)B·(B － ＜ B ＞)}ρHB

L*=i{HB，*}

当内禀系统可当作“热浴”处理时，ρHB=Z－1e－HB/kT，Z为配分函数，则有:

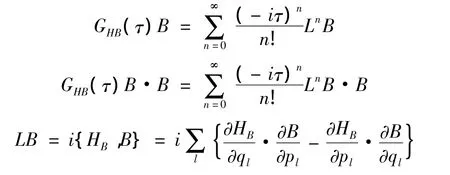
假设集体系统是一个具有单位质量的一维谐振子，集体系统和热浴的哈密顿量分别记作:

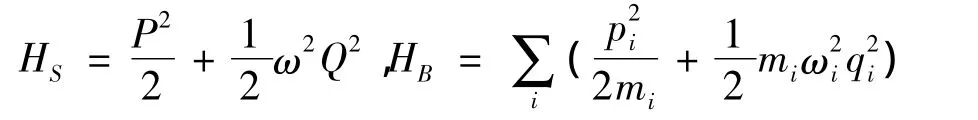
如果耦合作用是线性的，即HI=，则 B=，直接计算可得响应函数和关联函数分别为

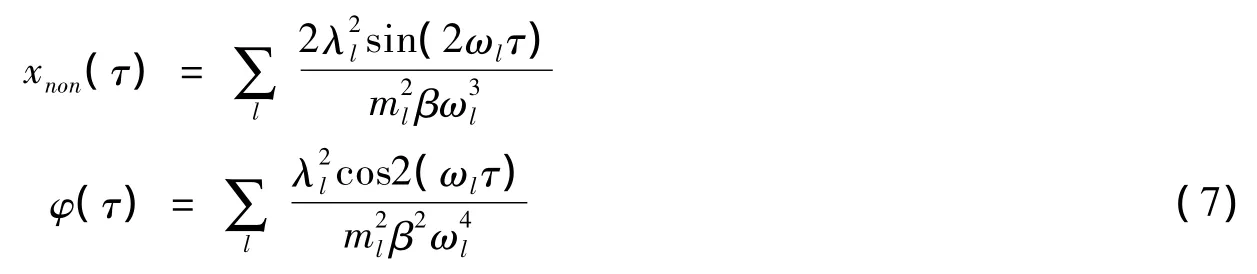
热浴中谐振子的频率可以看作是连续变化的，可以将对频率的求和化为对频率的积分。经过简单的推导可以得到频率分布ρ(ω)与谱密度J(ω)的关系。定义［8］

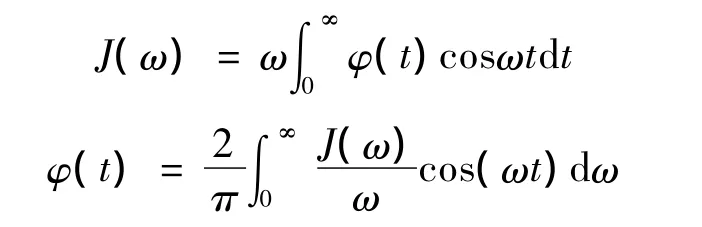
线性耦合时，可得频率分布与功率谱的关系为:

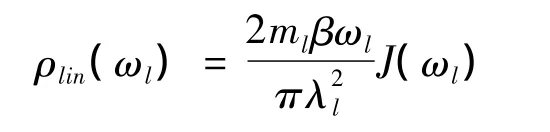
一般地，可以取 J(ω)=gαωα［9］，因此有:

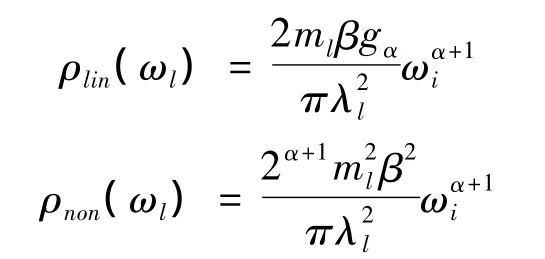
利用以上两式可得:

Ω'和Ω分别是热浴中振子的最小频率和最大频率。如果Ω'=0，Ω→∞，这时容易看出φlin(t)=φnon(t)，xlin(t)=xnon(t)，即线性耦合与非线性耦合的结果相同。如果α=1，则是通常所说的Ohmic扩散，此时 φlin(t)=φnon(t)=2gαδ(t)，如果 α≠1，则是反常扩散。

广义Langevin方程(1)是把内禀系统当作“热浴”处理后，在统计假设下得到的结果，与动力学方法得到的输运方程在最终形式上是一致的［10－14］。因此我们说，确实可以用唯像的输运方程来描述宏观平均运动。

(4)和(5)分别与(6)和(7)的形式一致，但推导过程完全不同，蕴含的物理意义也不相同。(4)和(5)是直接把内禀系统当作“热浴”处理后的统计结果，而(6)和(7)是从关联函数的动力学定义出发，然后再假设内禀系统满足正则分布的条件下得到的。因此，当内禀系统可以当作“热浴”处理时，集体系统的动力学关联和统计关联是一致的。

当内禀系统的自由度数非常大时，线性响应理论和非线性响应理论给出基本一致的结果，此时可把内禀系统当作服从正则分布的“热浴”。

［1］ Marumori T，Maskawa T，Sakata F，et al.Self－consistent collective－coordinate method for the large－amplitude nuclear collective motion［J］.Prog Theo Phys，1980，64:1294.

［2］ Cortes E，West B J，Lindenberg K.On the generalized Langevin equation:classical and quantum mechanical［J］.Chem Phys，1985，82(6):2708.

［3］ Lindenberg K，Cortes E.Thermal relaxation of systems with quadratic heat bath coupling［J］.Phys A，1984，126:489.

［4］ Caldeira A O ，Leggett A J.Quantum tunnelling in a dissipative system［J］.Ann Phys，1983，149:374.

［5］ Zwanzig R.Nonlinear generalized Langevin equation［J］.J Stat Phys，1973，9:215.

［6］ Pollak E，Berezhkovskii A M.Fokker－Planck equation for nonlinear stochastic dynamics in the presence of space and time dependent friction［J］.J Chem Phys，1993，92:1344.

［7］ Wu X，Sakata F，Zhuo Y，et al.Dynamic response function and large－amplitude dissipative collective motion［J］.Phys Rev C，1993，48:1183.

［8］ Weiss U.Quantum dissipative systems［M］.Singapore:World Scientific，1999.

［9］ Grabert H，Schramm P，Ludwig G.Localization and anomalous diffusion of a damped quantum particle［J］.Phys Rev Lett，1987，58:1285.

［10］ 汪志诚.热力学与统计物理［M］.北京:高等教育出版社，2003.

［11］ 苏汝铿.统计物理学［M］.上海:复旦大学出版社，1990.

［12］ 李如生.平衡和非平衡统计力学［M］.北京:清华大学出版社，1995.

［13］ Kubo R，Toda M，Hashitsume N.Statistical physicsⅡ，Solid State Science31［M］.New York:Springer－Verlag Berlin Heidelberg，1985.

［14］ Risken H.The Fokker－plank equation［M］.Berlin:Springer－Verlag Berlin Heidelberg，1984.