任意多连通截面扭转应力函数的温度场比拟解法

何 琳，王家林

(重庆交通大学土木建筑学院，重庆400074)

在涉及杆件的扭转问题时，求解扭件的应力、应变状态及抗扭刚度十分重要，它是强度、刚度分析和设计的基础。对于机械设备中的轴类扭件，像横截面为正三角形、圆、椭圆等形状简单、规则的特殊杆件扭转问题，可以采用圣维南逆解法或半逆解法获得解析解［1］。关于扭转问题多连通的变分法，林鸿荪也早有讨论。在土木结构工程中，大跨径桥梁主梁常采用薄壁箱形截面，因主梁截面的抗扭参数直接影响到结构的抗风稳定性，需要准确进行计算［2］。对于横截面形状复杂的杆件，为多连通域或不规则截面，截面的抗扭参数却难以求解，从而使其成为设计中的难题。许多研究者针对具体的工程问题，采用简化处理，给出各种近似的解决方法［3-7］。

笔者根据任意截面杆件扭转问题与二维稳态热传导问题在控制方程及边界条件形式上的相似性，提出了一种利用稳态温度场分析计算任意多连通截面扭转应力函数的直接比拟有限元方法。通过算例比较，表明此法可以避免“化复为单［7］”求解应力函数的缺陷，更便捷地解决各种截面的扭转问题。该方法理论概念明确、实用、精度高，具有通用性，为进一步计算任意复杂截面杆件的扭转刚度和应力等问题提供了新的有效手段。

1 杆件扭转问题的应力函数理论

1.1 等直杆扭转问题的控制微分方程

根据Prandt l应力函数理论，柱体扭转问题的域内控制微分方程和边界条件为［8］:

在域内:

沿边界:

式中:Φ(x，y)为Prandt l应力函数。

对于多连通截面，由于有多个边界，在各边界的取值可以不同，以Γ0表示截面的外边界，以Γi(i=1，…，n)表示各孔洞对应的内边界。则在各边界Γi(i=0，1，…，n)上，有:

由于应力函数增加或者减少一个常数，应力分量不受影响，因此不管是单连通截面还是多连通截面，均可令外边界Γ0上Φ=0(或其它常数)。对于多连通截面，理论上也可令应力函数在任意一个边界上取0或其它常数。

1.2 位移单值条件

对于多连通区域截面，由于只能指定一个边界上的应力函数为已知常数，其余边界上的应力函数属于未知常数，其相应的式(3)不能组成完备的定解条件，还需要补充位移单值条件才能构成完备的定解条件。

等直杆在扭转过程中，横截面的投影面发生刚性转动，即截面上的位移为:

式中:α为单位长度扭转角;w(x，y)反映了截面的翘曲情况。

对于位移w=w(x，y)，存在位移单值条件:

式(5)对任意环线均成立，Γ+表示沿环线的逆时针方向。

将式(5)应用于各边界，得到多连通截面上Prandtl应力函数的补充定解条件:

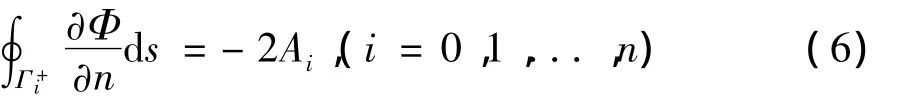
对于设置了应力函数为已知常数的边界，尽管式(6)仍然成立，但是由于位移单值条件自动得到满足，不必将对于该边界的式(6)作为定解条件。

综上所述，对于任意连通截面，Prandt l应力函数的完备定解条件如下。

1)在截面内，有:

2)在各边界 Γi(i=0，1，…，n)上Φ = Φi，但是只能在某一个Γk上设置应力函数的值:

3)对于Γk以外的边界Γi(i≠k)，有:

对单连通问题，由于只有一个边界，在外边界上取Φ=0，式(8)、式(9)自动得到满足。

2 稳态热传导理论

均质材料的二维稳态热传导问题所满足的控制方程［9］为:

式中:T为域内的温度函数;ρ为材料密度;Q为物体内部的热源密度;k为材料的热传导系数。

导热偏微分方程的定解条件有以下3类。

第1类边界条件是物体边界上的温度函数已知:

式中:Γ为物体边界，Γ方向为逆时针方向;¯T是已知温度值。

第2类边界条件是物体边界上的热流密度q已知:

第3类边界条件是已知与物体接触的流体介质温度Tf和换热系数α:

3 两类问题的比较

比较扭转问题控制方程(7)和二维稳态热传导问题的控制方程(10)不难发现:式(10)当取k=1、ρ=1和Q=2时与式(7)的形式完全相同。扭转问题边界条件式(8)类似于热传导第1类边界条件式(11)，扭转问题边界条件式(9)类似热传导第2类边界条件式(12)。

于是，基于两种问题在控制方程和定解条件方面的相近性，可采用比拟概念，使用通用有限元软件的稳态热传导模块计算对应的温度场来获得相应扭转问题的应力函数。在有限元软件ABAQUS中，具体的比拟方法为:

1)取二维稳态热传导问题的导热系数k=1、材料密度ρ=1、物体内部的热源密度Q=2，使二维稳态热传导问题的控制方程与扭转问题完全一致，此时扭转应力函数Φ对应于温度函数Τ。

2)对于截面的外边界，设置其温度为0。

3)对于各内边界，任取边界环线上一点为主控节点，通过绑定方式将环线上其它节点设置为主控节点的从节点，使得整条环线具有相同的温度，从而满足式(3)的条件。

4)多连通截面的位移单值边条件式(9)对应于热传导问题的第2类边界条件式(13)，从温度场角度，即是令各内边界上所有流入的热流值等于对应边界所围成的面积的两倍，在ABAQUS中的实现方法为:对于各内边界环线，任取环线上一点(一般可取主控节点)设置集中热流2Ai。

4 计算实例

下面给出单连通、复连通和多箱薄壁杆件3个实例的扭转分析，通过数值解与理论解的比较，充分验证了本方法的有效性与实用性。计算数据还验证了此法避免了文献［8］的缺陷，即在输入过大的热传导系数(如1010以上)时会带来计算上的不收敛现象，而在输入的热传导系数较小时(如105)，填充空洞域后，会带来填充域内温度的不等值现象。

4.1 圆环截面直杆扭转

扭杆截面如图1(a)，外径R1=2 m，内径R2=1 m。有限元计算网格如图1(b)。应力函数结果如表1。内外边界处，理论值和模拟计算数据完全一致，从A—B间，最大误差为0.000 526%。本实例结果表明，通过直接比拟热场分析来求解扭转问题的应力函数精确度非常高，且无需考虑填充材料热传导系数取值的问题。

图1 圆环形扭杆截面、沿A—B的应力函数Fig.1 Cross-section，finite element mesh and stress function along path A—B of annular torsion bar

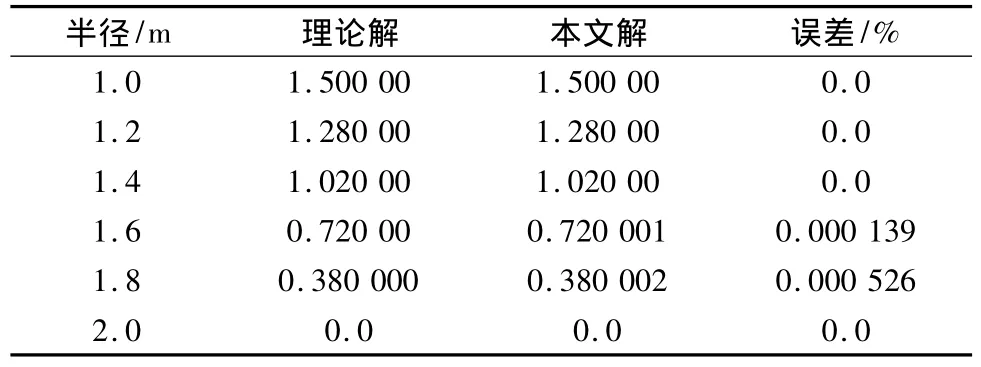
表1 圆环形扭杆截面A—B应力函数对比Table 1 Comparison of stress function along path A—B of annular torsion bar

4.2 矩形闭口薄壁杆件

如图2，矩形闭口薄壁杆截面，截面外边界长0.1 m，宽0.05 m，壁厚 0.005 m。采用直接比拟法求出的应力函数在截面内边界上完全一致，应力函数结果为1.570 5E-4，在相同的网格划分情况下，采用化复为单比拟解法，当填充材料的热传导系数取1.0E+10时，在截面的内边界上，各结点的应力函数结果为1.574 8E-4。两种比拟方法沿A—B的应力函数值(如图3)，除内边界稍差2.0E-8外，越往外边界计算结果越趋一致，最大误差值(在内边界处)为0.001 27%。

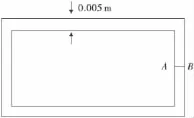
图2 矩形闭口薄壁杆截面Fig.2 Cross-section of closed thin-walled rectangular bar

图3 沿A—B的应力函数(×10－6)Fig.3 Stress function along path A—B(×10－6)

对图2的薄壁杆截面，根据薄壁柱体扭转的理论［8］可得到内壁应力函数值为 1.526 79E-4，与直接比拟法得到的结果1.570 5E-4误差2.78%，误差的原因在于薄壁柱体扭转中假设了薄壁沿厚度方向各处切应力相等，即应力函数法向梯度为常数。另一方面，误差较小表明此截面用薄壁柱体扭转理论处理具有可靠的精度。

4.3 多箱薄壁截面扭转

如图4，多箱矩形闭口薄壁杆截面，箱室具有不同的壁厚，其中 AB厚8 mm，CD厚12 mm，EF厚16 mm，GH及外壁厚10 mm。分别采用直接比拟法、化复为单的比拟解法(填充材料的热传导系数取1.0E+10)进行计算，表2为在截面3个箱室内边界上的应力函数结果。通过计算表明，两种计算方法的结果非常接近，应力函数值最大误差0.052 7%。同样地，文中方法不存在化复为单法存在热传导系数取值上的计算缺陷。

图4 三箱薄壁截面示意Fig.4 Cross-section of closed thin-walled rectangular bar with three boxes

表2 内壁应力函数值对比Table 2 Results comparison of stress function at inwall

5 结论

笔者通过比较二维稳态热传导问题和扭转问题控制方程及边界条件的相似性，提出了多连通任意截面直杆扭转问题的应力函数直接求解法，并利用有限元分析软件ABAQUS的稳态温度场分析功能，模拟求解了几种截面的扭转问题。计算结果表明，该方法简便实用，能精确地计算任意复杂截面杆件的扭转应力函数，不受截面形状的限制，可以避免化复为单求解扭转问题存在的材料特性取值缺陷，为进一步准确计算扭转问题的刚度和应力等问题提供了新的有效手段。

［1］程昌钧，王颖坚.弹性力学［M］.北京:高等教育出版社，1999:235-282.

［2］Cheng S H，LAu D T，Cheung M S.Comparison of numerical techniques for 3D flutter analysis of cable-stayed bridges［J］.Computers＆ Structures，2003，81(32):2811-2822.

［3］李金伯，何西泠，余国城.复杂形体轴的扭转刚度［J］.工程机械，1998，29(4):11-13.Li Jinbai，He xileng，Yu guocheng.Torsional rigidity of shafts of complex profile［J］.Construction Machinery and Equipment，1998，29(4):11-13.

［4］程耀芳，赖远明，王云峰.任意截面形状直杆扭转问题的解析解［J］.兰州铁道学院学报，1998，17(2):13-16.Cheng Yaofang，Lai Yuanming，Wang Yunfeng.Analytical solution of torsion problems of arbitrary shape cross section bars［J］.Journal of Lanzhou Railway University，1998，17(2):13-16.

［5］刘悦藏，范慕辉.凸多边形截面杆扭转问题的数值解法［J］.河北工业大学学报，1999，28(6):73-75.Liu Yuecang，Fan Muhui.The numerical method for solving the torsional shafts with convex polygon cross sections［J］.Journal of Hebei University of Technology，1999，28(6):73-75.

［6］李瑞選.多孔直杆扭转问题的边界元法［J］.华东理工大学学报，1995，21(5):640-647.Li Ruixia.Boundary element methods for elastic torsion of multihole bars［J］.Journal of East China University of Science and Technology，1995，21(5):640-647.

［7］李永奇，张卫红.模拟求解任意截面杆扭转的化复为单有限元方法［J］.兰州理工大学学报，2006，32(2):158-161.Li Yongqi，Zhang Weihong.A special simulation solution for torsional bars with arbitrary cross-section using finite element method［J］.Journal of Lanzhou University of Technology，2006，32(2):158-161.

［8］钱伟长，叶开沅.弹性力学［M］.北京:科学出版社，1956:143-152.

［9］孔祥谦.有限单元法在传热学中的应用［M］.北京:科学出版社，1986:1-7.