基于ANSYS的车桥耦合动力分析

谢秉敏，向中富，王小松，王少怀

(重庆交通大学土木建筑学院，重庆400074)

车辆通过桥梁时将引起桥梁结构的振动，而桥梁的振动又反过来影响车辆的振动，这种相互作用、相互影响的问题就是车辆与桥梁之间振动耦合的问题［1］。自1825年诞生于英国的第一条铁路起，人类对车辆与桥梁动力相互作用的探索就一直没有间断过。19世纪中期Willis提交了第一份桥梁振动响应研究的报告，探讨了由于车辆通过时产生的振动而导致Chester桥倒塌的原因，由此而揭开了研究车桥耦合振动内在机理的序幕［2-3］。

目前研究车桥耦合振动系统常用的分析方法有以下两种:①用直接积分法求解耦合车桥系统运动方程，但仅限于简单桥梁;②将车桥耦合问题处理成两组不同的运动方程，一组方程用于桥梁振动分析，另一个用于车辆振动分析，用轮与桥面竖向位移协调与相互作用力协调来使两个系统耦合在一起，适合于复杂结构体系桥梁、多自由度车辆模型的车桥耦合振动分析。国内学者大多应用有限元方法致力于后者的研究，但同时需编制复杂的专用程序计算［4］。

考虑到开发一套完善的有限元分析程序是一项浩繁的工作，不仅需要强大的技术支持，更需要大量的资金，越多越多的学者为了方便实用、避免编制复杂专用程序，开始应用大型通用结构分析软件进行研究。梁玉红［5］借助FORTRAN语言编写车辆动力方程求解程序，并将其作为ANSYS外部命令调用，实现列车过桥整个过程的动力响应分析。杨建荣，等［6］基于ANSYS前后处理器的强大功能，建立了桥梁有限元模型，结合自主程序VBDIP，形成了一个通用工具用于车桥耦合振动分析;施颖，等［7］利用ANSYS通过MATALAB进行迭代求解，从而为公路复杂桥梁动力性能评价提供了一种方便可靠的数值分析方法。

在以上的研究中，一般是通过外部软件来实现车辆微分方程的求解，将生成的车辆系统的数据文件再输入到ANSYS软件中完成桥梁系统的求解。但这样的数据交互十分麻烦，同时也是不必要的，因为基于ANSYS中APDL强大的功能，完全可以实现两子系统在ANSYS的迭代求解，实现数据的无缝交互。笔者以ANSYS为平台，利用其强大的前后处理功能，建立桥梁有限元模型，编写了基于Newmark-β法的车辆动力平衡方程的程序。在ANSYS环境下利用APDL语言实现了车辆上桥、车辆上桥轮对数、车辆出桥、车辆出桥轮对数及桥上轮对位置的判断等，最终实现了车辆上桥再出桥的车桥耦合振动响应计算。经过算例验证，该方法是正确有效的。

1 车桥耦合振动方程的建立

1.1 车辆振动方程的建立［8］

以整车4自由度车辆过简支梁桥为例，运用动力学中的达朗贝尔原理，可确定车辆运动自由微分方程，如图1。

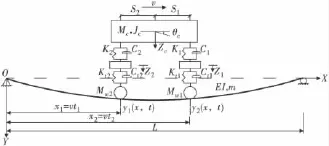
图1 4自由度车辆模型Fig.1 4 DOF vehicle model

车体竖向振动方程:

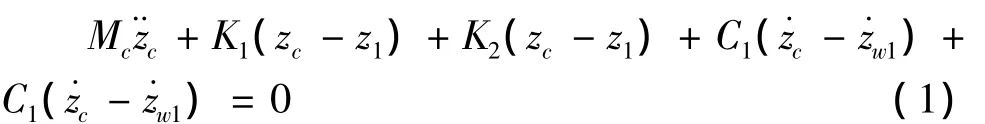
车体点头振动方程:

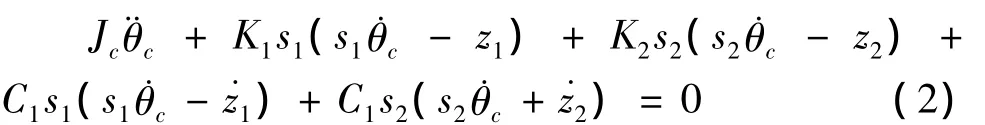
前轮对竖向振动方程:

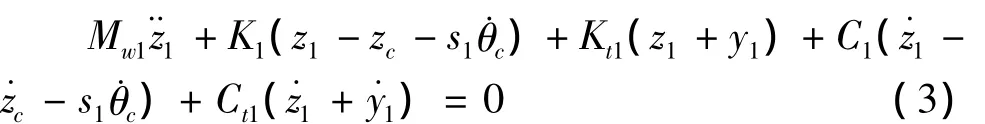
后轮对竖向振动方程:

式中:Zi，θi分别表示车体与转向架动力位移;Ki，Ci分别表示一系、二系弹簧刚度与阻尼;yi表示第i号车轮的竖向动力位移;Mi分别表示车体与转向架质量与抗转动质量矩;Jc为车体转动质量矩。

上述微分方程组经整理可写成如下矩阵形式:

式中:［Mv］，［Cv］，［Kv］分别为车辆的质量矩阵、阻尼矩阵和刚度矩阵;}分别为车体、转向架的竖向位移、速度、加速度列向量;［Fv］为车辆所受外力荷载向量。

1.2 桥梁振动方程的建立［9］

运用ANSYS强大的前后处理模块，近200种单元类型可方便地建立桥梁的有限元模型。

桥梁结构的振动方程可写为:

式中:［Mb］，［Cb］，［Kb］分别为桥梁的质量矩阵、阻尼矩阵和刚度矩阵;}分别为桥梁节点的竖向位移、速度、加速度列向量;［Fb］为桥梁所受外力荷载向量。

1.3 位移联系方程及车桥相互作用力方程

假设车轮在运行的过程中始终与桥面密贴不脱离，则可通过位移联系方程及车桥相互作用力将车桥两系统耦合起来。

轮对的位移可通过梁的相应位移表示，有:

式中:zvi为第i个车轮的竖向位移;zbi为第i个车轮所处桥梁上的位移，可通过Hermite插值得到;zir为第i个车轮处桥梁的不平整度及桥梁预拱度值;ui为车辆各轴悬挂弹簧的相对位移。

车桥的相互作用可通过轮胎与桥面间的相互作用力联系起来，有:

2 车桥耦合振动分析流程及算例

2.1 分析流程

运用ANSYS中的APDL工具，实现车桥耦合振动流程如下:

1)利用ANSYS建立桥梁结构有限元模型;

2)输入车辆参数;

3)假设车辆上桥的初始状态，如位移、速度、加速度等;

4)判断上桥的车辆数及轮对数，提取t时刻桥梁振动响应，通过插值计算，得到轮对运动参数zi，，更新车辆运动方程荷载项若车辆出桥则进行第8);

5)利用Newmark-β法求解t时刻车体响应;6)根据最新的车体响应更新桥梁运动方程荷载项

7)求解t+Δt时刻桥梁振动响应。重复第4);

8)绘制桥梁节点时程曲线。

2.2 算例1——单元数量对求解结果的影响

由于车辆系统在梁上不断运动，使车桥系统耦合振动响应是一组时变性二元二阶微分方程，求解十分复杂且数据量较大，为简化起见，以图2中移动车轮+簧上质量过简支梁桥为例，通过振型叠加法选择适当的阶数对方程组进行解耦求解，与利用ANSYS求解进行对比，以验证文中方法的正确性。

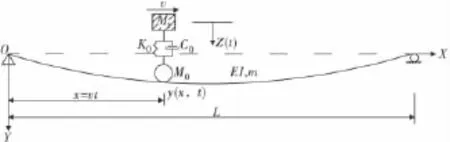
图2 车轮+簧上质量模型Fig.2 Sprung mass model

图2中，L为简支梁跨径，取16 m;EI为简支梁抗弯惯性矩，取2.5×1010m2;简支梁线质量 m取9 360 kg/m，泊松比 μ 取0.2;移动质量 M0=1.69×104kg，簧上质量 M1=4.69 ×104kg，弹簧刚度 K0=4.87×106N/m;连接阻尼系数 C0=3.14×105N·s/m;同时假定车辆以60 km/h匀速通过。

将简支梁桥采用Beam3单元模拟，划分为不同单元数量，通过ANSYS求解与采用振型叠加法通过MATLAB进行数值求解的结果对比如图3～图5及表1。

图3 跨中位移时程曲线Fig.3 Displacement histories at the middle strip

图4 节点速度时程曲线Fig.4 Velocity histories at the middle strip

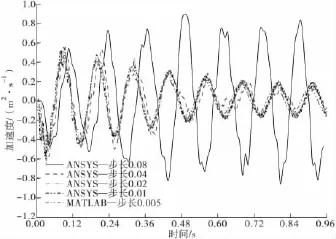
图5 跨中加速度时程曲线Fig.5 Acceleration histories at the middle strip

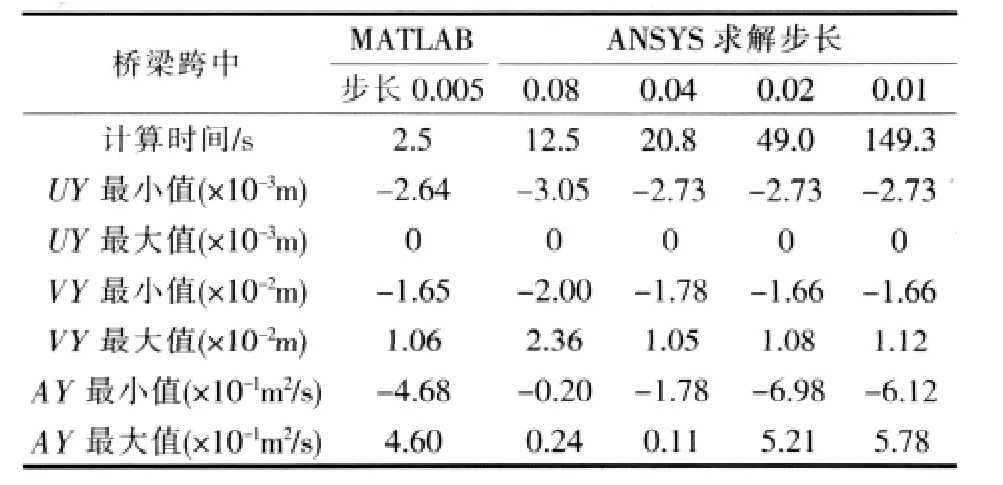
表1 计算结果对比Table 1 Comparison of results

从图3～图5及表1可以发现，利用ANSYS求解时，对给定的桥梁而言，时间步长对结果的影响十分显著。当时间步长过大时，其求解结果与真实值偏差较大;随着时间步长不断减小，结果是越精确的，但精度提高的不多，同时求解时间也大幅提高。针对算例中的16 m简支梁，求解的时间步长取为0.02 s是较为合适的。

2.3 算例2——车辆以不同车速通过桥梁

仍采用算例1中车辆及桥梁参数，桥梁仍用Beam3单元模拟，时间步长取为0.02 s。车辆以60 km/h，180 km/h通过桥梁。结果对比如图6～图8。

图6 跨中位移时程曲线Fig.6 Displacement histories at the middle strip

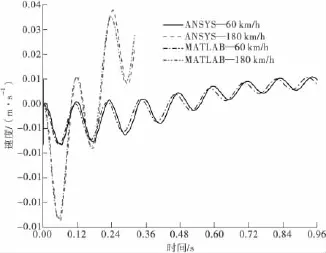
图7 跨中速度时程曲线Fig.7 Velocity histories at the middle strip

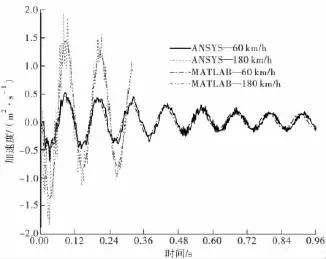
图8 跨中加速度时程曲线Fig.8 Acceleration histories at the middle strip

由图6～图8分析可发现:基于笔者思路编制的ANSYS求解结果与采用振型叠加法的求解结果是相吻合的，其中位移与速度时程曲线几乎重合，而ANSYS求解的加速度时程曲线与采用振型叠加法求解的时程曲线趋势一致，数值在后者附近振荡，同时在车速较高时，ANSYS计算的桥梁竖向加速度在极值点处数值较后者偏大。这是因为在前面的利用振型叠加法求解车桥振动耦合的理论推导中，只考虑了桥梁的第一阶振型，而忽略了后续各阶振型的贡献，从而在数值上有偏差。

从以上两个算例中的分析，说明了文中方法的正确性，可以为工程界解决车桥耦合问题提供某种新的思路。

3 结语

ANSYS作为广泛应用的大型通用有限元程序，笔者在ANSYS平台上，利用其丰富的单元类型可方便的建立各种桥梁结构，进行车桥动力耦合分析，从而避开了编制复杂的专用程序。

从算例来看，笔者所提出的方法较为准确。由于桥梁单元数量对结果影响较大，推荐桥梁结构采取每10 cm一个单元的策略，这样可以获得较满意的解。

在车速较高时，桥梁加速度极值点处有振荡，比理论求解结果稍大。但从数值结果上看，精度还是令人满意的，可以为工程界开展车桥动力问题的分析提供某种简单易行的方法。

［1］李小珍，强士中.列车-桥梁耦合振动研究的现状与发展趋势［J］.铁道学报，2002，24(5):112-120.Li Xiaozhen，Qiang Shizhong.State-of-the-art review and trend of studies on vehicle-bridge interaction［J］.Journal of the China Railway Society，2002，24(5):112-120.

［2］Biggs I M.Introduction to Structrual Dynamics［M］.NewYork:MC-Graw-Hill Book Co.，Inc.，1964.

［3］夏禾，张楠.车辆与结构动力相互作用［M］.北京:科学出版社，2005.

［4］单德山，李乔.车桥耦合振动分析的数值方法［J］.重庆交通学院学报，1999，18(3):14-20.Shan Deshan，Li Qiao.The numerical method for studying the interaction vibration between bridge and vehicle［J］.Journal of Chongqing Jiaotong University，1999，18(3):14-20.

［5］梁玉红.用ANSYS实现车桥耦合空间振动分析［D］.石家庄:石家庄铁道学院，2005.

［6］杨建荣，李建中，范立础.基于ANSYS的车桥耦合振动分析［J］.计算机辅助工程，2007，16(4):23-26.Yang Jiangrong，Li Jianzhong，Fan Lichu.Analysis on vehiclebridge coupling vibration based on ANSYS［J］.Computer Aided Engineering，2007，16(4):23-26.

［7］施颖，宋一凡，孙慧，等.基于ANSYS的公路复杂桥梁车桥耦合动力分析方法［J］.天津大学学报，2010，43(6):537-543.Shi Ying，Song Yifan，Sun Hui，Zhou Xinping，et al.Dynamic analysis method of vehicle-bridge coupling for complicated bridges based on ANSYS［J］.Journal of Tianjin University，2010，43(6):537-543.

［8］王福天.车辆动力学［M］.北京:中国铁道出版社，1994.

［9］王勖成.有限单元法［M］.北京:清华大学出版社，2003.