铝合金型材挤压模工作带长度优化方法研究

董桂伟，温道胜，赵国群

（山东大学材料科学与工程学院，山东济南250061）

0 引言

在铝合金型材挤压成形过程中，模具出口处型材挤压速度的均匀性主要受导流室、分流室形状、尺寸和工作带长度的控制。工作带又称定径带，是型材挤压模中垂直模具工作端面并用以保证挤压制品形状、尺寸和表面质量的区段。由于工作带的摩擦阻力可以调整金属流速，在导流室、分流室形状和尺寸一定的条件下，合理设计不等长的工作带长度，可以有效提高型材断面各个部分金属的流速均匀性，从而减少挤压过程中的附加应力和挤压后工件内的残余应力，防止型材的变形与开裂。

目前，计算设计型材挤压模工作带长度的方法主要有补充应力法[1]和在生产实践中总结出的一些经验算法[2]等。这些方法主要是通过大量的实验或实际生产中得到的经验知识对工作带长度进行反复修正，不但不能全面准确地反映其内在关系，而且周期长、成本高。本文提出一种铝合金型材挤压模具工作带长度的数值优化设计方法，该法以有限体积法数值模拟技术为基础，在课题组现有铝型材挤压非正交网格有限体积法数值模拟系统-AE_FVM系统[3]的基础上，建立了挤压模具工作带长度优化设计模型，对优化过程进行了较详细的描述，并通过实例分析对优化结果进行了模拟验证。

1 工作带长度优化设计

1.1 型材上的边界条件

工作带长度对铝型材挤压速度的影响可通过摩擦边界条件和温度边条件等的施加来实现。以摩擦边界条件为例，在铝型材成形过程中，型材截面上各点的速度以及型材流出模具出口时的形状都会受工作带摩擦的影响。图1给出了铝型材边界上面网格单元中心节点的切向速度与相邻体网格单元中心节点的速度之间的关系。

图中，LPB为边界面单元中心节点与相邻体单元中心节点之间的法向距离，vP为体单元P的速度矢量，vPt、vPn分别为切向和法向的速度分量。假设铝型材区域摩擦边界条件中的摩擦系数为材料与模具之间的摩擦系数mf，面单元中心节点B的动力粘度系数为μB，材料的剪切屈服应力为σS，采用狄力克雷边界条件[4-6]，得到面单元中心节点的切向速度可表示为：

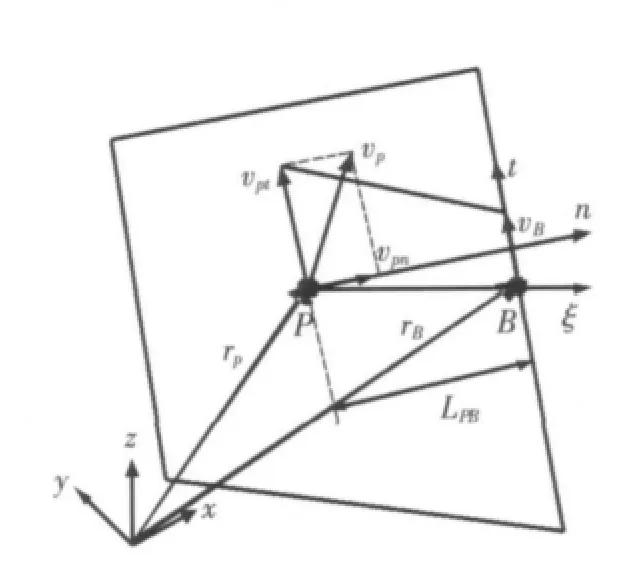
图1 摩擦边界节点切向速度示意图

1.2 工作带分段

为了使型材横截面上各点的速度均匀，必须根据型材的结构和几何尺寸以及挤压模具的结构调节工作带长度。在调节工作带长度之前，需要对工作带进行合理的分段。以壁厚为2mm的U型实心型材为例，其挤压模具工作带可按同心圆法则[4]进行分段，如图2所示。

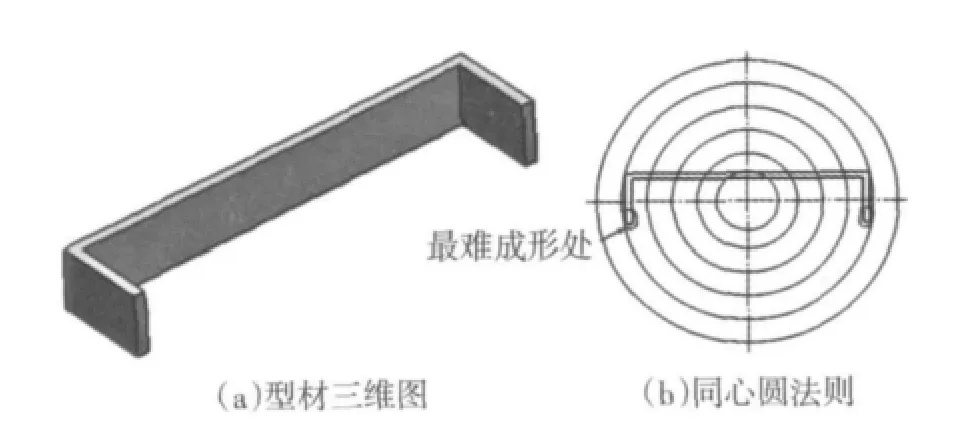
图2 U型型材挤压模具工作带的分段方法

同心圆法则为：①将型材断面上材料成形最困难的地方设为参考点，如图2b所示，工作带在参考点处的长度可初步设置为该处型材壁厚的1.5～2倍。②与参考点处工作带相邻的工作带长度比参考点处的工作带长度多1mm。③如果型材各处的壁厚相同，那么如图2b所示，在同一个同心圆环内的工作带长度相同。如果型材各处的壁厚不相同，则以同心圆圆心为基准点每相距10mm工作带长度依次减少。

这里的同心圆法则只是铝型材挤压模具工作带分段和长度设置的参考之一，在实际生产中还要根据挤压型材的结构和尺寸并结合试模情况对工作带进行调整。另外，将工作带分段后，为了便于型材上边界条件的施加，必须对每段工作带进行识别，识别方法根据AE_FVM系统采用的结构网格的特点进行[7-10]。

1.3 收敛判据

根据铝型材实际生产中的经验，当型材在挤压模具出口处的最大与最小挤压速度之差不超过平均挤压速度的10%时，型材的挤压速度可视为均匀。为了表征型材截面上挤压速度的均匀性，可采用以下公式来判定：

v¯——整个型材截面上的平均速度。

假设第n段型材对应的工作带长度为ln，Δl为与工作带接触的型材网格在挤压方向上的单位网格尺寸。根据模拟结果和Flagvn判断是否要对第n段型材对应的工作带长度进行调节。当 Flagvn＞0.1时，若 Flagvn＜0，则 ln=ln-Δl；若 Flagvn＞0，则 ln=ln+Δl。当Flagvn≤0.1时，则ln保持不变。当 Flagvn≤0.1（n=1～N）同时各段工作带长度 0＜ln≤L 时（L 为最大工作带长度），则说明此时的工作带长度为优。工作带长度自动优化的流程如图3所示。

经优化，最终收敛的结果为最优工作带长度，即Flagvn≤0.1。但是，工作带长度调节对型材挤压速度的影响是有限的，也就是工作带长度调节属于微调。当工作带长度调节无法使型材挤压速度达到要求时，如工作带长度经自动优化后出现ln≤0或者优化前后所有的ln都无变化时，则需要考虑调节导流室或分流室的形状和尺寸。

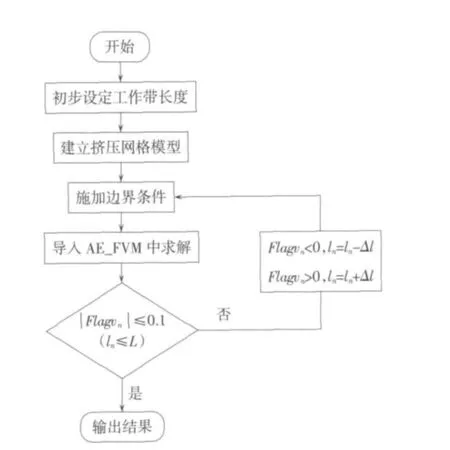
图3 工作带长度自动优化流程图

2 实例分析

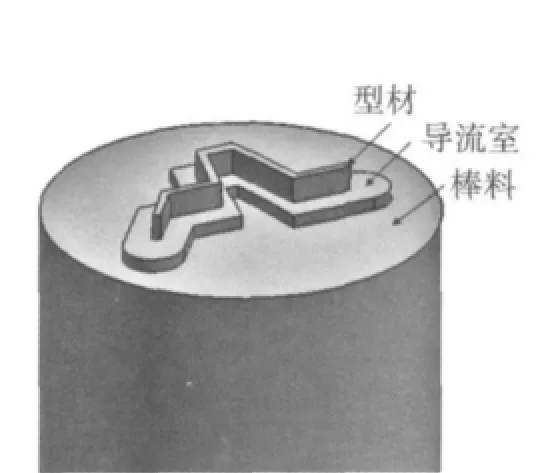
图4 挤压模型三视图

图5 型材及导流室尺寸

为了检验建立的工作带长度优化模块的可行性，本节以图4所示的挤压模型为例进行工作带长度自动优化模拟。挤压模型中的型材和导流室尺寸（单位为mm）如图5所示，棒料尺寸为 ø150mm×300mm。根据同心圆法则并参考实际生产过程，可将型材分为6段区域对应14段工作带，如图6所示。

本算例中采用的材料是铝合金AA6063，材料参数如表1所示，挤压参数如表2所示。在模拟过程中，AE_FVM采用的网格模型如图7所示。为了便于对型材挤压速度进行分析，在型材截面上选取30个特征点，如图8所示。

假设每段型材对应的工作带长度相等，根据工作带长度的设置原则并结合实际生产中工作带长度的设置，初步设置各段型材对应的工作 带 长 度 为 ：区 域 1，4.2 mm;区域 2，5.6mm;区域 3，7.0 mm;区域 4，7.0mm;区域 5，5.6 mm；区域 6，5.6mm。

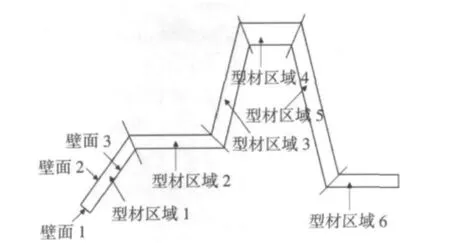
图6 型材分段

表1 挤压材料参数

表2 挤压参数

图7 AE_FVM采用的网格模型

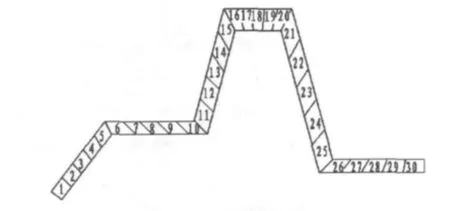
图8 型材截面上的特征点

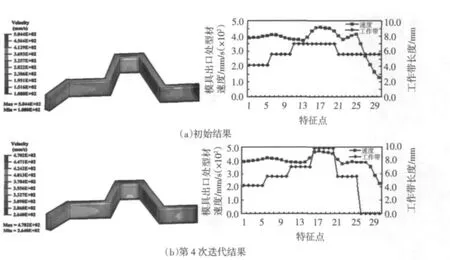
图9 工作带长度初次自动优化结果

图10 迭代过程中型材各区域对应Flagvn的值

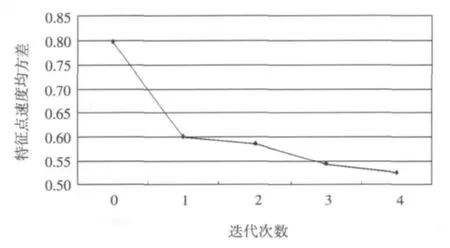
图11 特征点速度均方差

经AE_FVM对挤压模具工作带长度的初次自动优化结果如图9所示。从图9中可看出，区域4处的挤压速度最大，而区域6处的挤压速度相对较小。图10显示，在初始工作带长度下型材区域4与型材区域6对应的 Flagvn都大于0.1，并且它们对应的Flagvn分别大于零和小于零，这说明型材区域4与型材区域6对应的工作带长度需要优化，具体的优化方法如图3所示。图11显示，型材截面上特征点的速度均方差随工作带长度自动优化的进行而逐渐减少，这说明随着工作带长度自动优化的进行，型材在模具出口的速度逐渐变得均匀，同时这也验证了本文建立的工作带长度自动优化模块的可行性。同时，从图9可看出，四次迭代后型材区域4对应的工作带长度在时已经达到了9.8mm（最大长度），型材区域6对应的工作带长度变为0mm，这说明通过调节工作带长度已无法使型材在模具出口处的挤出速度达到要求，因此要考虑调节导流室的形状和尺寸。

根据图9中工作带长度的初次优化结果，调节导流室的形状和尺寸（单位为mm），如图12所示。

图13给出了导流室形状和尺寸调节后工作带长度的优化结果。可以看出，型材区域4对应的 Flagvn在第二次迭代后其值达到0.099，此时每段型材对应的Flagvn都在-0.1～+0.1范围之内，同时每个型材区域对应的工作带长度都大于0mm并且小于等于9.8mm，这说明工作带长度经自动优化后已达到要求。

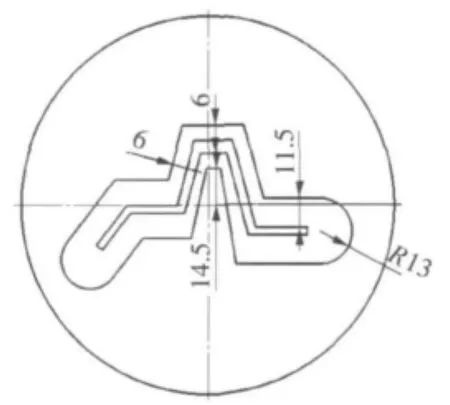
图12 形状和尺寸调节后的导流室

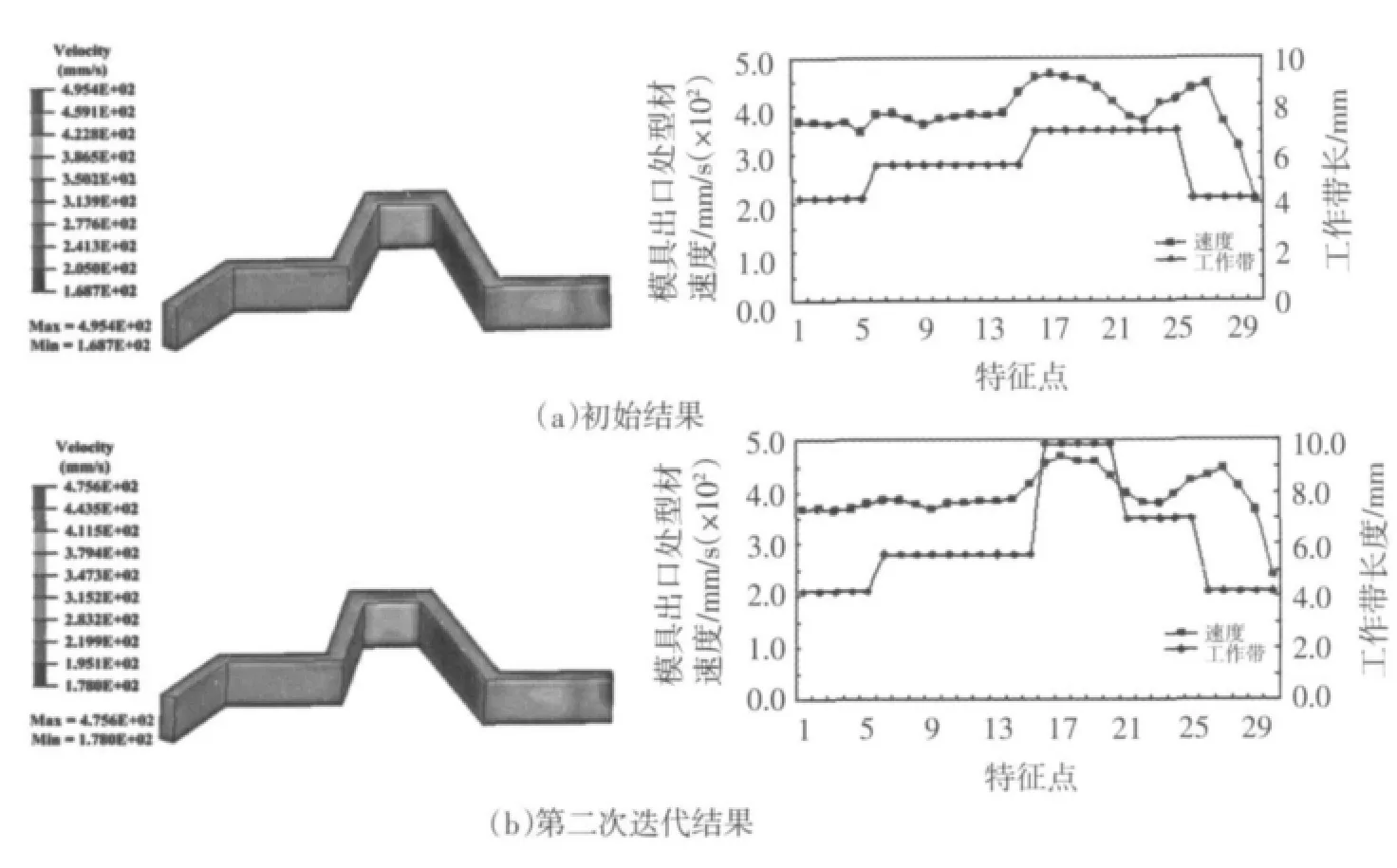
图13 导流室形状和尺寸调节后工作带长度自动优化结果

3 结论

本文在课题组现有的铝型材挤压非正交网格有限体积法数值模拟系统AE_FVM系统基础上建立的优化设计模块能够进行型材挤压模具工作带长度的优化设计，结合数值模拟技术，验证表明优化结果是有效的。

[1]刘静安.铝型材挤压模具设计、制造、使用及维修[M].北京：冶金工业出版社，1999.

[2]解英艳，宋 力.铝型材挤压模具工作带长度的合理选择与计算[J].机械设计与制造，1995，（3）：1-3.

[3]王 锐.铝型材挤压非正交网格有限体积法数值模拟关键技术[D].山东大学博士学位论文，2009.

[4]周 飞，苏 丹，彭颖红，等.有限体积法仿真金属塑性成形的基本理论[J].上海交通大学学报，2002，36（7）：2-4.

[5]黄克坚，包忠诩，周天瑞.有限体积数值模拟技术在铝型材挤压变形规律研究中的应用[J].轻合金加工技术，2003，31（4）：29-31.

[6]李大永，王洪俊，罗 超，等.薄壁铝型材挤压有限体积法分步模拟[J].上海交通大学学报，2005，39（1）：6-9.

[7]Williams A.J.，Croft T.N.，Cross M.Computational modeling of metal extrusion and forging process[J].Journal of Processing Technology，2002，125-126：573-582.

[8]陈 浩，赵国群，张存生，等.薄壁空心铝型材挤压过程数值模拟及模具优化[J].机械工程学报，2010，46（24）：34-39.

[9]王福军.计算流体动力学分析-CFD软件原理与应用[M].北京：清华大学出版社，2004.

[10]段庆林，李锡夔.成型填充过程的任意拉格朗日-欧拉有限元与无网格自适应耦合模拟[J].机械工程学报，2007，43（7）：120-127.