对《圆形有界磁场问题的分类及解析》文中一个解答的补充

周平原

（临海市回浦中学 浙江 台州 317000）

《圆形有界磁场问题的分类及解析》［1］文中的例9，解答不够完整，这里给予补充和更正.题目及原解答如下.

【题目】如图1所示，半径为R的圆筒形区域内，分布着磁感应强度为B，方向垂直纸面向里的匀强磁场.一带正电的微粒从圆筒壁上小孔A点沿半径方向射入磁场，且初速度方向垂直于磁场方向.若该微粒与筒壁碰撞时不损失电荷量，并能以大小相等的速度反向弹回，问初速度大小满足什么条件时，微粒能回到A点，并求出微粒回到A点所经历的时间.已知微粒的质量为m，电荷量为q，不计微粒重力.

图1

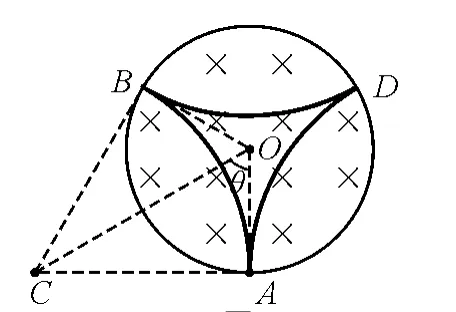
图2

解析：如图2所示，设微粒经n－1次碰撞，飞行n段圆弧后回到A点，设∠AOC＝θ，则

可得初速度满足

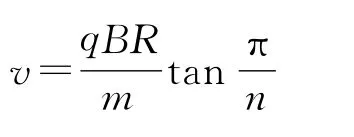
的条件时，微粒能回到A点，其中n取大于2的整数.

设微粒回到A点所经历的时间为t，周期为T，圆弧对应的圆心角∠ACB＝α，则

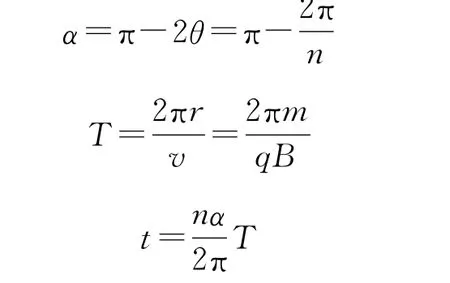
三式联立可得

注意：只有加上“微粒能绕圆筒壁一周后回到A点”的附加条件，上述解答才是完整的.否则应设微粒绕圆筒壁k周，经n－1次碰撞，飞行n段圆弧后回到A点，设∠AOC＝θ，则

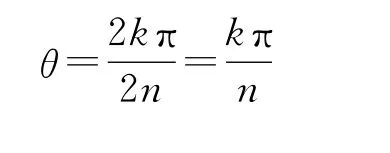
微粒轨迹半径

可得初速度满足

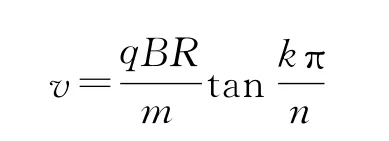
的条件时，微粒能回到A点，其中n＝3，4，5，…，k＝1，2，3，…，因圆弧对应的圆心角必大于零，所以，还要满足的条件.另外，当值相等时，求出的初速度值都是相同的，这时，只有数值最小的这组k，n才与微粒实际发生的运动相符，因为当微粒回到A点时，就会从小孔射出圆筒外，不会再循环运动下去.

接下去再求微粒回到A点所经历的时间t，设圆周运动的周期为T，A圆弧对应的圆心角∠ACB＝α，则

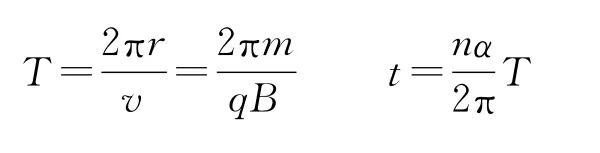
三式联立可得

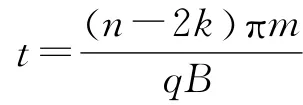
k，n的取值同样要满足上面的要求.

1 周平原.圆形有界磁场问题的分类及解析.物理通报，2011（10）：43～47