基于逆算符方法的谐波注入式SPWM技术
郑春芳 张 波 丘东元 余向民
(1.广东机电职业技术学院 广州 510515 2.华南理工大学电力学院 广州 510640)
1 引言
SPWM控制技术[1]是逆变器研究和应用领域的核心技术之一,从最初采用模拟电路产生 PWM信号到目前的全数字化方案,各种不同的SPWM技术相继出现[1-5]。由于描述自然采样 SPWM 的数学模型是超越方程,采用常规的数值解法求解起来要花费较多时间,因此自然采样法的数学模型一直被认为不适合用于实时控制。文献[6]介绍了逆算符方法对自然采样SPWM的适用性,用逆算符方法推导出了单极性和双极性自然采样 SPWM 开关点的解析表达式,并根据计算精度要求得到开关点的近似解析解,从而为自然采样SPWM技术的实时应用提供理论依据。
当逆变器用于交流电机驱动时,为弥补SPWM技术电压利用率只有 0.866的不足,人们提出了谐波注入式SPWM技术[7-14],即人为地在各相调制基准正弦波中掺入一定分量3的整数倍次谐波,以提高电压利用率。由于描述谐波注入式SPWM的数学模型仍是超越方程,常规数值解法耗时较多,不利于实时控制。基于文献[6]的理论,本文尝试采用逆算符法求取谐波注入式SPWM开关点解析表达式,并以注入3次谐波的SPWM为例,利用逆算符法求出它们相应的解析表达式,探讨所得到的3次谐波注入式 SPWM 开关点解析表达式在实际应用中的有效性。
2 逆算符方法
2.1 逆算符方法的基本原理[15]
逆算符方法的基本原理如下。
将待解方程表示为下面逆算符形式

式中,g代表方程的非奇次部分;u为待解的变量;F为逆算符,它又可以表示为

式中,L代表F中线性部分可逆算子,可表示多种数学运算,例如u的微分;R是其余线性算子;N为非线性部分。
将式(2)代入式(1),有
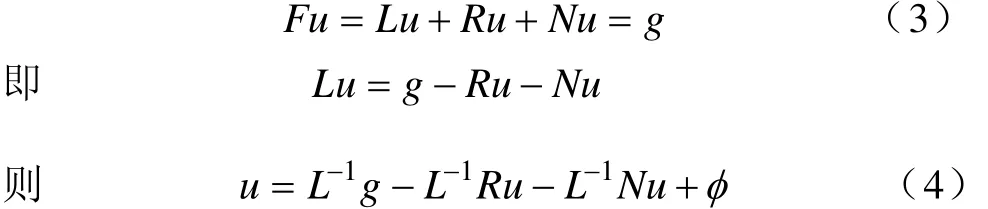
式中,φ 满足Lφ=0,它对应于初始或边界条件。
将u和Nu分别分解为

式中,An(u0,u1,…,un)被称为Adomian多项式。
则式(4)可写为
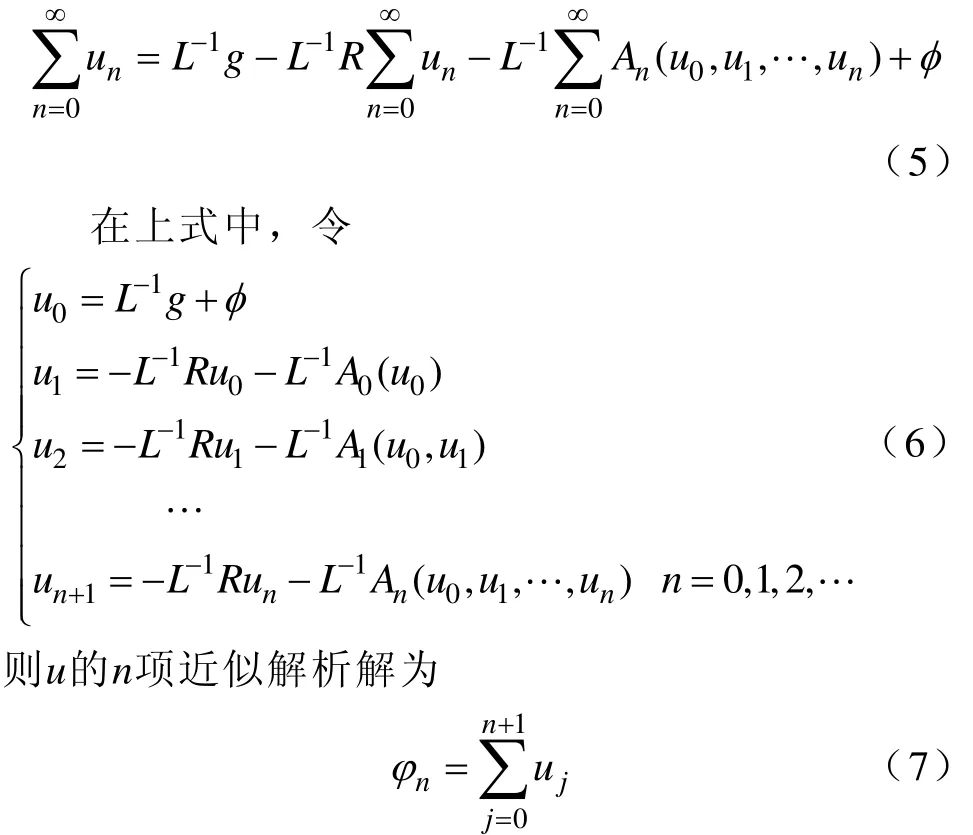
显然,当n→∞时,φn→u,则φn为u的解析解。
该解析解的收敛性已由Cherruault等人所证明[16,17]。实际运算中,n取3~6项,近似解析解φn就逼近真解。
2.2 φn的求解
由式(6)可知,由初始条件或边界条件求出u0后,u1,u2,…,便可依次求得。因而,求解φn的一个关键技术就是如何确定Adomian多项式An。
文献[17]给出了确定An的具体推导过程以及部分具体的的An表达式,这里仅列出一些具体的Adomian多项式

因此,由式(8)和式(6)即可求出φn。
3 谐波注入式SPWM开关点的解析式
3.1 3次谐波注入式SPWM开关点方程
谐波注入式 SPWM 法就是在正弦波调制波中加入一定比例的零序谐波,即3倍频谐波的一种调制方法。它能使得调制波呈现马鞍形,以降低调制波幅值,增大直流电源电压的利用率,同时又能使逆变器具有良好的谐波抑制特性。
以注入3次谐波为例,假设注入幅值为x的3次谐波,不失一般性,正弦调制波的周期为T=2π,初相为零时期望的调制波函数可表示为

式中,m为调制比,即为相电压基波幅值与载波幅值之比;x为注入的3次谐波系数。
对式(9)求导并令其为零,可得



对式(11)进行求导可得

求解式(12)得:x1=1/6,x2= -1/3。
显然负值解不符合条件,代入式(12)时,幅值会大于1,所以x=1/6,此时其所对应的调制比可以达到最大值1.154 7,因此谐波注入式SPWM调制波为

这里以自然采样双极性SPWM如图1所示为例,则3次谐波注入式SPWM方法中开关点方程可以分别表示为

式中,k=2N/π;N为载波比,且对于双极性SPWM,N=2π/Tc;Tc为三角载波的周期;m=Um/Ucm为调制比;Urm为正弦调制波峰值,Ucm为三角载波幅值。

图1 自然采样双极性SPWM示意图Fig.1 The sketch of bipolar NSPWM
3.2 3次谐波注入式SPWM开关点的逆算符表达式及其解析解
式(14)可表示为逆算符形式

其中求三角载波下降沿与正弦调制波的交点时a=(4i-4)/k,b= -m/k;求三角载波上升沿与正弦调制波的交点时a=(4i-2)/k,b=m/k;k=2N/π(i=1,2,…,N)。
因而,参照2.2节,可得出自然采样双极性3次谐波注入式SPWM开关点解析解为


虽然式(16)的解析解表达式是一个无穷项的迭加,但由于其收敛性惊人的快,因此取其前3~6项就可以作为3次谐波注入式SPWM开关点的近似解析解[18]。
如取n=1,则3次谐波注入式SPWM的开关点解析解为

4 解析式实用性分析
4.1 收敛速度和精度
为了验证用逆算符方法得出的3次谐波注入式SPWM开关点解析表达式的收敛情况,本节首先用常规的牛顿迭代法求解3次谐波注入式SPWM开关点方程式(15),算法中初始值取式(15)中的a,迭代误差取小于1e-6(如果希望开关点的近似值更加接近精确值,可以将迭代误差取得更小),计算得到开关点的近似值。然后将用牛顿迭代法得到的开关点近似值作为开关点的自然采样准确值,以便对式(16)取不同项Adomian多项式时开关点解析解的计算精度及收敛速度作比较。
由于谐波注入式SPWM一般用于三相逆变器,为了避免基波与变频谐波频率接近而发生跳动,并得到较好的三相脉宽调制波形,N一般取3的奇整数倍[19]。因而这里取m=1、分别对N=15、21进行计算来说明采用逆算符方法求解谐波注入式 SPWM开关点的收敛速度。计算中分别取n=1,2,3项Adomian多项式作为开关点t的近似解析解,由于在正弦波周期内SPWM脉冲对称,所以只需计算前1/4正弦波的开关点,计算结果见附录中的附表1和附表2。附表1和附表2中还列出了用逆算符方法取不同项 Adomian多项式得到的开关点相对于自然采样准确值的绝对误差(小数点后都取六位小数),从表中不难看出,当载波比N固定时,取Adomian多项式的项数越多,误差就越小;当计算Adomian多项式的项数相等时,载波比 N越大,误差就越小,即随着 N的增大,只要取较少项Adomian多项式计算得到的开关点就越接近自然采样准确值。
4.2 谐波抑制能力
图2给出了载波比N=15、21下取不同项数Adomian多项式的SPWM的各次谐波抑制能力曲线。某次谐波抑制能力可以表示为[20]

式中,Vj为第j次谐波幅值;V1为基波幅值。Y越大,表示谐波抑制的效果越好。
根据逆算符方法计算得到的开关点,利用傅里叶分析算出各次谐波的幅值(根据波形的对称性,这里只考虑除3及3的整数倍次谐波外的奇数次谐波),然后再按式(19)计算,从而获得各次谐波抑制能力。从图2看出,取Adomian多项式的项数越多,其谐波抑制能力就越接近自然采样法。
通过对不同载波比下取不同项Adomian多项式得到的3次谐波注入式SPWM开关点的精度对比及其各次谐波抑制能力曲线分析表明,只要选取适当项数的Adomian多项式,采用逆算符方法求得的开关点就能非常接近于自然采样开关点,以符合实际需要。
5 结论

图2 N=15、21下取不同项数Adomian多项式的谐波注入式SPWM的各次谐波抑制能力曲线Fig.2 The ability of eliminating harmonics for HISPWM by choosing different terms of Adomian polynomials at N=15,21
本文采用逆算符方法,推导出3次谐波注入式SPWM开关点的解析表达式,其表达式由无穷项Adomian多项式表示,可以根据需要的计算精度要求选择合适的Adomian多项式项数来求解3次谐波注入式SPWM的开关时刻。由不同载波比下3次谐波注入式SPWM开关点解析解的精度分析实例可知,随着载波比的增大,只要取较少项Adomian多项式计算得到的开关点就越接近自然采样准确值,有利于3次谐波注入式SPWM的数字化实现。
附 录

附表1 载波比N=15,m=1下谐波注入式SPWM的开关点Apptab.1 The switch-points of HISPWM when N=15,m=1

(续)
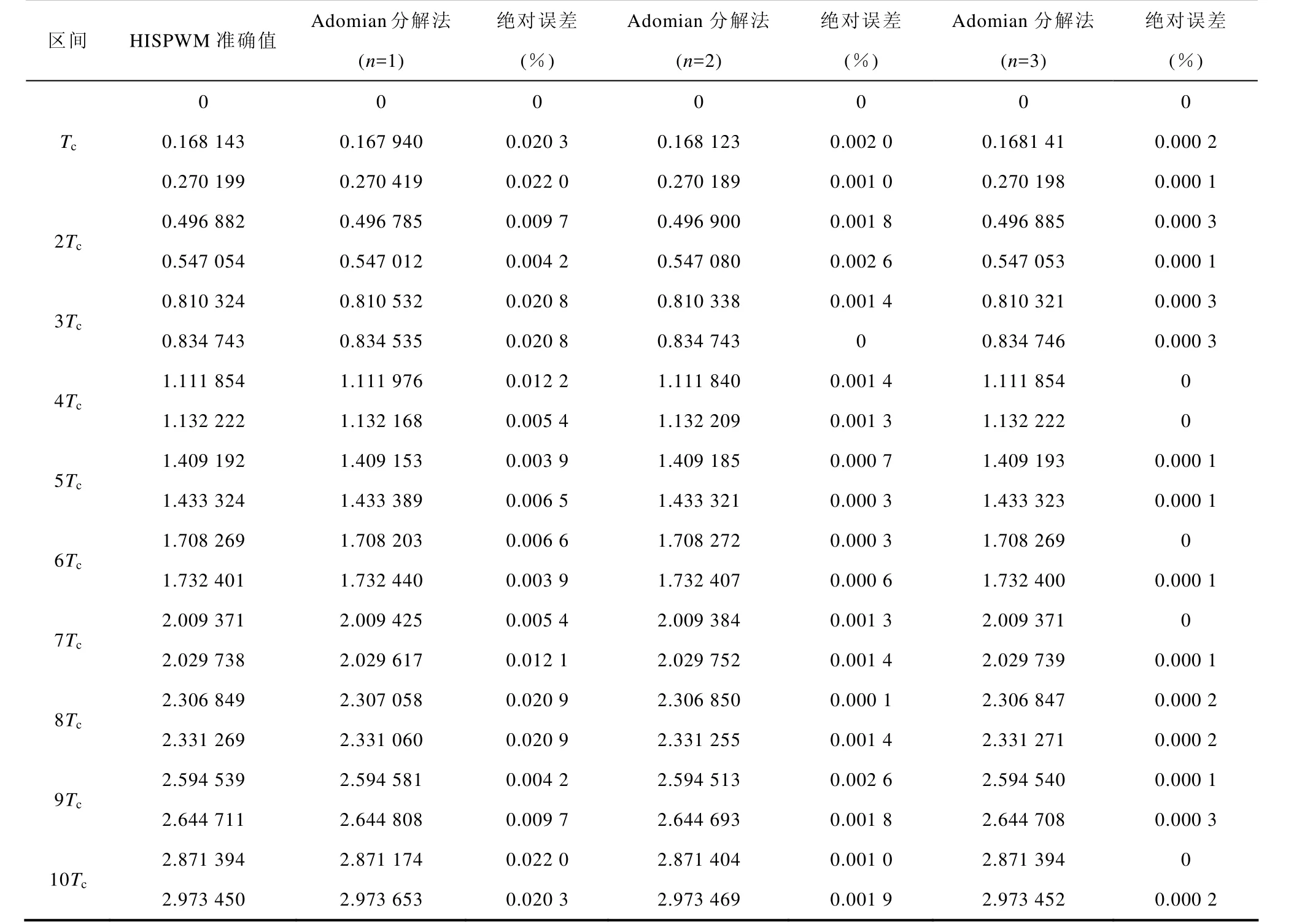
附表2 载波比N=21,m=1下谐波注入式SPWM的开关点Apptab.2 The switch-points of HISPWM when N=21,m=1
[1]Hamman J, Van Der Merwe F S.Voltage harmonics gene-rated by voltage-fed inverters using PWM natural sampling[J].IEEE Transactions on Power Electronics, 1988, 3(3): 297-302.
[2]张艳莉, 费万民.基于重心重合原则的数字化多电平SPWM方法[J].南京理工大学学报(自然科学版),2010, 34(3): 209-302.Zhang Yanli, Fei Wanmin.Digitalized multilevel SPWM method based on cg-superpostition theorem[J].Journal of Nanjing University of Science and Technology(Natural Science), 2010, 34(3): 209-302.
[3]朱良合, 邹云屏, 唐健.基于线性采样的SPWM研究与实现[J].电力电子技术, 2010, 44(8): 58-59.Zhu Lianghe, Zou Yunping, Tang Jian.Research and implementation of SPWM based on linear-sampling strategy[J].Power Electronics, 2010, 44(8): 58-59.
[4]陈增禄, 毛惠丰, 周炳根, 等.SPWM数字化自然采样法的理论及应用研究[J].中国电机工程学报,2005, 25(1): 32-37.Chen Zenglu, Mao Huifeng, Zhou Binggen, et al.A study on theory and application of digital natural sampling based SPWM[J], Proceedings of the CSEE,2005, 25(1): 32-37.
[5]李扶中, 熊蕊.一种新型的不对称规则SPWM采样法[J].电力电子技术, 2007, 41(4): 93-95.Li Fuzhong, Xiong Rui.A novel sampling mehtod of SPWM with nonsymmetrical rules[J].Power Electronics, 2007, 41(4): 93-95.
[6]郑春芳, 张波, 丘东元.基于逆算符方法的数字化自然采样SPWM技术[C].中国电源学会全国电源技术第17届年会, 2007: 323-326.
[7]Bowes S R.Regular-sampled harmonic elimination/mini-mization PWM techniques[C].IEEE Applied Power Electronics Conference, 5th Annual, 1990:532-540.
[8]Wen Inne Tsai, York Yih Sun.Design and implementation of three phase HIPWM inverters with instantaneous and average feedback[C].Proceedings of the IEEE Annual Conference of the Industrial Electronics Society, 1993: 800-805.
[9]EI Kassas I A, Hulley L N, Shepherd W.Microprocessor based PWM inverter with third harmonic injection[C].Proceedings of 1995 International Conference on Power Electronics and Drive Systems, 1995, 2: 555-559.
[10]Duran M J, Salas F, Arahal M R.Bifurcation analysis of five-phase induction motor drives with third harmonic injection[J].IEEE Transactions on Industrial Electronics, 2008, 55(5): 2006-2014.
[11]Arahal M R, Duran M J.PI tuning of five-phase drives with third harmonic injection[J].Control Engineering Practice, 2009, 17(7): 787-797.
[12]李小青, 陈国柱.基于3次谐波无源注入法的谐波抑制技术[J].电力系统自动化, 2007, 31(14): 61-65.Li Xiaoqing,Chen Guohu.An approach to harmonic suppre-ssion based on triple harmonics injection with passive circuit[J].Automation of Electric Power Systems, 2007, 31(14): 61-65.
[13]谢峰, 关振宏, 吴桢生, 等.基于3次谐波注入的级联多电平逆变器[J].电源技术应用, 2009, 12(02): 7-9.Xie Feng, Guan Zhenhong, Wu Zhensheng, et al.Cascaded multilevel inverter based on three harmonic injection mehtod[J].Power Supply Technologies an Applications, 2009, 12(02): 7-9.
[14]官二勇, 宋平岗, 叶满园.基于3次谐波注入法的三相四桥臂逆变电源[J].电工技术学报, 2005, 20(12): 43-45.Guan Eryong, Song Pinggang, Ye Manyuan.Three-phase inverter with four bridge: legs based on three harmonic injection method[J].Transactions of China Electrothechnical Society, 2005,20(12): 43-45.
[15]Adomian G.Stochastic system[M].New York:Academic Press, 1983.
[16]Cherruault Y.Convergence of adomian’s method [J].Kybernets, 1988, 9(2): 31-38.
[17]Cherruault Y, Adomian G.Decomposition method: a new proof of convergence [J].Mathematical and Computer Modelling, 1993, 18(12):103-106.
[18]Adomian G.Nonlinear stochastic operator equations[M].Academic Press, 1986.
[19]刘凤君编著.正弦波逆变器[M].北京: 科学出版社,2002.
[20]钟福金, 钱昱明, 王晓军.交流变频调速系统的SPWM波形生成方法的谐波分析[J].南京航空航天大学学报, 1994(增刊26): 94-98.Zhong Fujin, Qian Yuming, Wang Xiaojun.Harmornic analysis of methods forming SPWM wave in VVVF System[J].Transactions of NanJing University of Aeronautics, 1994,(sup26): 94-98.

