基于计算全息的菲涅尔双随机相位加密技术

于娜娜

（中国海洋大学 信息科学与工程学院，山东 青岛266100）

近年来，随着计算机技术的不断革新，信息技术快速发展，社会信息化程度大大提高，大量数据通过网络进行传递，其中数字信息占了很大的比例，因此图像数据传输中的保密性越来越受到重视。现有的比较成熟的加密技术中，计算机加密，量子加密等加密方法保密性差且硬件成本高，光学加密方法具有高速、并行、大信息量等特点，而且光波具有振幅、相位、波长、偏振等特性可用于加密方面，因此光学信息处理的应用研究受到国内外很多学者的关注，特别是数字图像的光学加密技术得到广泛研究[1-4]，但是这些加密方法都是输出一个复值图像，大多数情况下，不便于加密图像的存储、记录与输出。

傅里叶计算全息[5-6]是一种较为成熟的全息术，它的主要特点是记录一个复数光场的频谱，并且能够再现原图像的共轭，本文是在计算机中，应用菲涅尔双随机相位加密系统，对数字图像进行加密，以傅里叶计算全息记录加密图像，利用傅里叶计算全息再现加密图像的共轭，将其引入菲涅尔衍射光路解密，经过正确密钥解密得到原图像。解密过程中，两个随机相位板，两次菲涅尔衍射的距离及加密过程应用的光波长都可作为解密密钥，而且计算全息记录图的再现加密图像共轭提取，极大的提高了图像加密的安全性，而且解决了复值加密图像难存储及传输的问题。

1 图像的加密理论和计算方法

1.1 图像加密的理论模型

图像加密的理论光路图（如图1所示）是一个菲涅尔衍射双随机相位加密[7-8]光路和一次傅里叶变换光路。

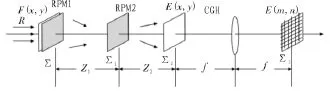
图1 图像加密理论光路图Fig.1 Scheme of image encryption theory

原始数字图像F（x，y）是一个复数矩阵，将其置于加密光路输入平面∑，引入单位振幅的垂直入射光R照射，并放置第一个随机相位板RPM1紧贴输入平面，出射光波首先受到RPM1的调制加密，然后经过一次距离为Z1的菲涅尔衍射到达第一菲涅尔衍射平面∑1，在该平面受到第二个随机相位板RPM2的调制加密，再进行一次距离为Z2的菲涅尔衍射到达输出平面∑2完成加密。但是该加密图像为一复值矩阵，难以存储、传输以及保存，本文应用比较成熟的傅里叶计算全息记录加密图像，对该加密图像的频谱进行编码，将该复值矩阵转化为一实值的计算全息图，并且该图像为一幅隐藏了原图像大小尺度信息的全息图E（m，n），在传输过程中更具有一般性，增加了图像传输的安全性。

1.2 图像的解密过程

根据光路的可逆性，解密过程为加密的逆过程，图像解密的光路图如图2所示。

图2 图像解密理论光路图Fig.2 Scheme of image decryption theory

解密过程中，将计算全息加密图像E（m，n）置于输入平面，引入单位振幅的垂直入射光R′照射计算全息加密图，经过一次傅里叶变换，再现得到原加密图像及其共轭，由于菲涅尔双随机相位加密系统的特性，将计算全息加密图像再现的原加密图像共轭引入菲涅尔双随机解密系统，分别经过Z3=Z2，Z4=Z1的两次菲涅尔衍射以及两个随机相位板RPM3=RPM2，RPM4=RPM1的调制解密，在输出平面∑得到原始图像。

1.3 傅里叶计算全息加密图像的设计制作

本文采用罗曼Ⅲ型编码方法[9]，分别对加密图像频谱的振幅、相位进行编码，输出光场分布 E（m，n）为复数，记为则相应的振幅为相位为arctan（-Amn/Bmn）。计算全息图编码的一个离散抽样点（如图3所示）。

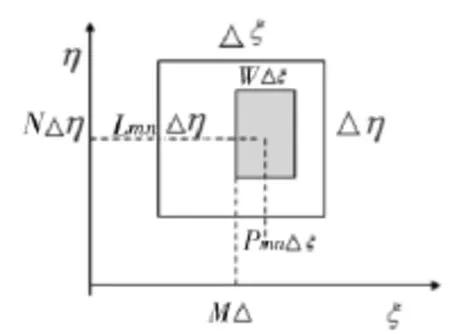
图3 罗曼Ⅲ型编码单元Fig.3 Coding unit of RomanⅢtype

整个CGH共有M×N个抽样单元，图3为其中一个抽样单元。其中（m，n）为该单元的横纵坐标；△ζ、△η为抽样单元边长。深色部分为通光孔径，面积Lmn△ζ×W△η编码该单元通光强度，反映频谱振幅信息，罗曼Ⅲ型编码方式中，W不变，使Lmn与振幅成正比；由不规则光栅对相位调制原理，通光孔径中心与该抽样点中心的距离Pmn与该点相对相位成正比，以达到用Lmn编码振幅和用Pmn编码相位。

在计算全息的编码过程中，在对输出图像的频谱振幅编码时，对幅值A作归一化处理，以保证全息图中各抽样单元中的通光矩形孔高度不超过记录单元高度；在对频谱相位进行编码时，当φ>π/2时，在程序中采用“模式溢出校正法”，以防止与邻近的矩形孔发生重迭而造成计算全息图再现时产生失真；在实现图像加密解密以及计算全息制作过程中，在编码前用Matlab中的移频函数fftshift（）将频谱的高频部分移到靠近中心的部分，以完成计算机中正确的傅里叶变换[10]。制得到计算全息加密图像如图 4（c）所示，图 4（a）为待加密图像，通过对比两图可见，计算全息加密图是一幅隐藏了原图像尺度大小信息的白噪声的图像，传输中更具有一般性，提高了图像加密及传输的安全性。

2 图像加密和解密的实验设计与分析

为了检验该数字图像加密方法的实用性，文中利用Matlab7.1对该方法进行了计算机实验。计算机实验的过程涉及离散傅里叶变换和相位板“调制”效果。用计算机中Matlab的离散傅里叶变换函数和计算机生成的随机矩阵与光场复振幅分布的点乘积模拟相位板 “调制”。 根据傅里叶计算全息再现共轭像的特性，针对该共轭像对该图像加密方法的有效性进行了检验。

2.1 傅里叶计算全息记录加密图像

用罗曼Ⅲ型编码方法，对菲涅尔衍射双随机相位加密图像（如图4（a）所示）的频谱编码，制作傅里叶计算全息图（如图 4（c）所示）。

图4 图像Fig.4 Image

图4（a）为待加密图像“熊猫”，图 4（b）为菲涅尔衍射双随机相位加密图像，是一幅随时间统计无关的白噪声图像，图4（c）是傅里叶计算全息加密图像，是一幅隐藏了原图像尺度大小信息的图像，在传输过程中更具有一般性。

2.2 傅里叶计算全息加密图像的再现

傅里叶计算全息图记录原加密图像的频谱，所以再现过程中，以垂直入射光照射计算全息图，出射光场经过一次透镜的傅里叶变换，再现图像（如图5所示）。

傅里叶计算全息再现图像特性，图中+1级单元为原加密图像，-1级单元为原加密图像的共轭，菲涅尔衍射双随机相位加密系统的特性，需要原加密图像的共轭作为解密图像，所以本文利用傅里叶全息的再现图像特性，将该单元引入解密光路解密。

2.3 图像解密密钥实验

图5 傅里叶计算全息加密图再现像Fig.5 Reproduced image of encrypted Fourier computer-generated hologram

利用图2图像解密理论光路，将图5中-1级傅里叶计算全息再现单元引入解密光路，对图像加密的各个密钥进行了解密实验，加密过程中，作为解密密钥的各参数：P1，P2为随机相位板，λ=0.63 μm，Z1=Z2=0.3 m，解密结果图像如下，图 6（a）是正确密钥解密图像，即Z4=Z3=Z1=Z2=0.3解密结果图像；图6（b）是 Z3为错误密钥，选取Z3=0.305解密结果图像；图 6（c）是Z4为错误密钥，选取Z3=0.301解密结果图像；图6（d）是P3为错误密钥，即P3≠P2解密结果图像；图6（e）是P4为错误密钥，即 P4≠P1解密结果图像；图 6（f）是解密波长 λ=0.631 μm时解密结果图像；图6（g）是针对整个计算全息图再现像解密结果图像。

通过图6可见，各解密密钥正确时能很好地解密获得原图像，衍射距离 Z1、Z2，相位板 P2，应用波长都可作为解密密钥，而且相对Z1，Z2精度要求更高，由于所取解密图像光强图，P1不可作为解密密钥，同时计算全息图再现多个图像单元，增加了不知解密密钥时的解密难度。

3 结 论

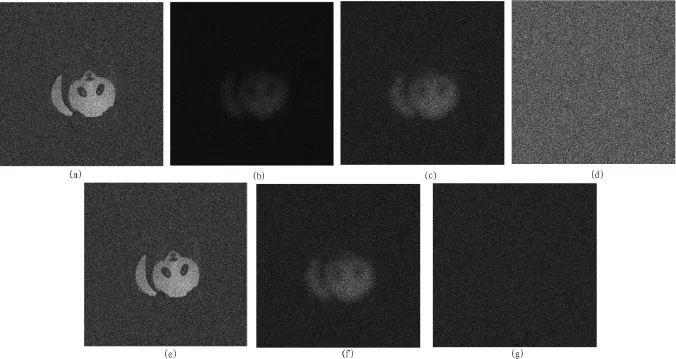
图6 解密图像Fig.6 Decrypted image

文中以菲涅尔衍射系统双随机相位图像加密技术为基础，结合傅里叶计算全息技术记录加密图像，利用傅里叶计算全息图再现的特性，针对再现的加密图像共轭解密，克服了普通菲涅尔衍射系统双随机相位图像加密方法加密图像难记录的问题，省去了制作加密图像共轭的过程，增加了不知解密密钥时解密的难度。两个随机相位板、应用波长、两次菲涅尔衍射距离都可作为解密密钥，经过加密的傅里叶计算全息图是一幅隐藏了原图尺度大小信息的图像，该加密图像在传输过程中更具有一般性，因此，该方法提高了图像加密以及传输的安全性。可广泛应用于图像加密、机要文件加密保存、光学信息安全等领域。

[1]Joshi M，Shakher C，Singh K.Fractional Fourier plane image encryption technique using radialhilbertand Jigsaw transform[J].Optics and Lasers in Engineering，2010（48）:754-759.

[2]张怡霄，罗克简，黄奇忠，等.彩虹标识的计算全息加密[J].四川大学学报，2000，37（1）:51-54.ZHANG Yi-xiao，LUO Ke-jian，HUANG Qi-zhong，etal.Rainbow hologram encryption using CGH [J].Journal of Sichuan University，2000，37（1）:51-54.

[3]张怡霄，黄奇忠，杜惊雷，等.计算全息干涉实现防伪和信息的加密存储[J].应用激光，1999（4）:156-158.ZHANG Yi-xiao，HUANG Qi-zhong，DU Jing-lei，et al.Anti-counterfeiting and encryption storage of information using CGH interference[J].Applied Laser，1999（4）:156-158.

[4]张州，刘国.使用计算全息进行三维信息加密的方法研究[J].光学技术，2007（34）:8-10.ZHANG Zhou，LIU Guo.A 3-D Encryption technique using computer generated hologram[J].Optical Technique，2007（34）:8-10.

[5]金国藩，等.计算机制全息图[M].北京:清华大学出版社，1984.

[6]Kishk S，Javidi B.Information hiding technique with double random phase encoding[J].Appl.Opt，2002，41（26）:5462-5470.

[7]He M Z，Qai L Z，Liu Q.Almutiple image encryption and water-marking by random phase matching[J].Optics，2005，247（7-12）:29-37.

[8]何龙庆.基于MATLAB的计算全息术的研究 [J].巢湖学院学报，2008，10（6）:66-72.HE Long-qing.Study on computer generated hologram under MATLAB[J].Jounal of Chaohu Co1lege，2008，10（6）:66-72.

[9]孙欣，黄永峰，席思星，等.基于计算全息的真彩色全息术[J].光学学报，2009，29（12）:1-5.SUN Xin，HUANG Yong-feng，XI Si-xing，et al.True color holographic technology based on computer generated holography[J].Opt.Lett，2009，29（12）:1-5.